RKI 


Долгожитель
|
    
Цитата: vikycik написал 16 окт. 2009 17:44
51. Даны законы распределения независимых случайных величин:
X -4 0 4 Y 2 4
P 0,1 0,5 0,4 P 0,5 0,5
Найти М(Z), если Z = 3X + Y/2.
Варианты ответов:
1)5 2)6,6 3)4,2 4)5,1 5)1
M(X) = (-4)*(0.1) + 0*(0.5) + 4*(0.4) = - 0.4 + 0 + 1.6 = 1.2
M(Y) = 2*(0.5) + 4*(0.5) = 1 + 2 = 3
M(Z) = M(3X + Y/2) = M(3X) + M(Y/2) = 3M(X) + M(Y)/2 =
= 3*(1.2) + 3/2 = 3.6 + 1.5 = 5.1
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 16 окт. 2009 19:02 | IP
|
|
bga

Новичок
|
     
приветик)помогите решить 2 задачки...взаранее спасибо))
1.Определить закон распределения дискретной случайной величины,если известна ее дисперсия,причем x1<x2<x3<x4.Определить M(X).Если x1=2, x2=x2, x3=10, x4=14, p1=0.2, p2=p2, p3=0.4, p4=0.1 D(X)=13.44
2.Определить вероятность того,что нормально распределенная случайная величина X принимает значения,находящиеся в интервале (A,B)(альфа и бета),если математическое ожидание равно a,а среднее квадратическое отклонение -G(сигма).если a=13, G=4, A=7, B=16.
(Сообщение отредактировал bga 16 окт. 2009 19:59)
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 16 окт. 2009 19:57 | IP
|
|
vikycik

Новичок
|
    
в 40 задаче при x->бесконечность
|
Всего сообщений: 34 | Присоединился: сентябрь 2009 | Отправлено: 16 окт. 2009 20:30 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: vikycik написал 16 окт. 2009 17:44
40. F(x) является функцией распределения некоторой случайной величины. Сколько утверждений из числа перечисленных являются справедливыми в любом случае?
1)F(x) непрерывна справа;
2) предел F(x) =0 при x->бесконечность;
3)интеграл от F(x) по всей числовой прямой равен 1;
4)F(x) строго монотонна на всей числовой прямой.
Варианты ответов:
1) 0 2) 1 3) 2 4) 3 5) 4.
верных нет
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 16 окт. 2009 21:08 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: bga написал 16 окт. 2009 19:57
1.Определить закон распределения дискретной случайной величины,если известна ее дисперсия,причем x1<x2<x3<x4.Определить M(X).Если x1=2, x2=x2, x3=10, x4=14, p1=0.2, p2=p2, p3=0.4, p4=0.1 D(X)=13.44
X 2 x2 10 14
P 0.2 p2 0.4 0.1
0.2 + p2 + 0.4 + 0.1 = 1
0.7 + p2 = 1
p2 = 0.3
X 2 x2 10 14
P 0.2 0.3 0.4 0.1
M(X) = 2*(0.2) + (x2)*(0.3) + 10*(0.4) + 14*(0.1) =
= 0.4 + (0.3)(x2) + 4 + 1.4 = 5.8 + (0.3)(x2)
M(X^2) = 4*(0.2) + ((x2)^2)*(0.3) + 100*(0.4) + 196*(0.1) =
= 0.8 + (0.3)((x2)^2) + 40 + 19.6 = 60.4 + (0.3)((x2)^2)
D(X) = M(X^2) - (M(X))^2 =
= 60.4 + (0.3)((x2)^2) - (5.8 + (0.3)(x2))^2 =
= 60.4 + (0.3)((x2)^2) - (33.64 + 3.48(x2) + (0.09)(x2)^2) =
= 60.4 + (0.3)(x2)^2 - 33.64 - 3.48(x2) - (0.09)(x2)^2 =
= (0.21)(x2)^2 - 3.48(x2) + 26.76
D(X) = 13.44
(0.21)(x2)^2 - 3.48(x2) + 26.76 = 13.44
(0.21)(x2)^2 - 3.48(x2) + 13.32 = 0
(0.07)(x2)^2 - 1.16(x2) + 4.44 = 0
7(x2)^2 - 116(x2) + 444 = 0
x2 = 6
M(X) = 5.8 + (0.3)(x2) = (5.8) + (0.3)*6 = 5.8 + 1.8 =
= 7.6
2.Определить вероятность того,что нормально распределенная случайная величина X принимает значения,находящиеся в интервале (A,B)(альфа и бета),если математическое ожидание равно a,а среднее квадратическое отклонение -G(сигма).если a=13, G=4, A=7, B=16.
 = \Phi(\frac{16 - 13}{4}) - \Phi (\frac{7 - 13}{4}) = )
 - \Phi (-1.5) = \Phi (0.75) + \Phi (1.5) \sim )
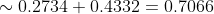
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 16 окт. 2009 21:29 | IP
|
|
TheCard

Новичок
|
    
Добрый день. Помогите решить 3 задачи, если не сложно.
1.Среди 50 деталей 3 нестандартные. Наугад достали 2 детали. Найти вероятность того, что они нестандартные.
2.Составить закон распределения числа попаданий в цель при четырех выстрелах, если вероятность попадания приодном выстреле равна 0.1
3.Расчитать вероятность появления хотя бы одного А при 10 независимых опытах от вероятности Р появления события А в каждом опыте для р=0.05
Заранее спасибо
|
Всего сообщений: 3 | Присоединился: октябрь 2009 | Отправлено: 17 окт. 2009 13:30 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: TheCard написал 17 окт. 2009 13:30
1.Среди 50 деталей 3 нестандартные. Наугад достали 2 детали. Найти вероятность того, что они нестандартные.
Посчитаем число n всевозможных исходов. Способов выбрать 2 детали из 50 имеющихся:
n = C(2;50) = 50!/48!2! = 1225
A = {две нестандартные детали}
Посчитаем число m исходов, благоприятных событию A. Способов выбрать 2 детали из имеющихся 3 нестандартных:
m = C(2;3) = 3!/2!1! = 3
По классическому определению вероятности
P(A) = m/n = 3/1225
2.Составить закон распределения числа попаданий в цель при четырех выстрелах, если вероятность попадания приодном выстреле равна 0.1
Случайная величина X - число попаданий в цель при 4 выстрелах.
n = 4
p = 0.1 - вероятность попадания в цель при одном попадании
q = 1 - p = 1 - 0.1 = 0.9
Случайная величина X имеет распределение Бернулли с параметрами n = 4 и p = 0.1
P(X=0) = (0.9)^4 = 0.6561
P(X=1) = C(1;4)*(0.1)*((0.9)^3) = 4*(0.1)*(0.729) = 0.2916
P(X=2) = C(2;4)*((0.1)^2)*((0.9)^2) = 6*(0.01)*(0.81) = 0.0486
P(X=3) = C(3;4)*((0.1)^3)*(0.9) = 4*(0.001)*(0.9) = 0.0036
P(X=4) = (0.1)^4 = 0.0001
Ряд распределения случайной величины X имеет вид:
X 0 1 2 3 4
P 0.6561 0.2916 0.0486 0.0036 0.0001
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 17 окт. 2009 14:25 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: TheCard написал 17 окт. 2009 13:30
3.Расчитать вероятность появления хотя бы одного А при 10 независимых опытах от вероятности Р появления события А в каждом опыте для р=0.05
n = 10 - количество испытаний
p = 0.05 - вероятность появления события A при одном испытании
q = 1 - p = 1 - 0.05 = 0.95
m - количество появлений события A при 10 независимых испытаниях
P(m >= 1) = 1 - P(m < 1) = 1 - P(m=0) = 1 - (0.95)^10 ~ 0.4013
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 17 окт. 2009 14:28 | IP
|
|
TheCard

Новичок
|
    
Огромное спасибо. Вы меня выручили.
|
Всего сообщений: 3 | Присоединился: октябрь 2009 | Отправлено: 17 окт. 2009 14:45 | IP
|
|
TheCard

Новичок
|
    
И еще одна, забыл про нее, последняя
Для нормальной работы автобазы на линии должно быть не менее 8 автомобилей. Всего имеется 10 авто. Для работы автобазы нужно как минимум 8 автомобилей, вероятность невыход авто на линию составляет 0.1 . Найти вероятность нормальной работы автобазы на следующий день.
И опятьже заранее спасибо.
|
Всего сообщений: 3 | Присоединился: октябрь 2009 | Отправлено: 17 окт. 2009 14:51 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности