Sav

Новичок
|
    
Помогите пожалуйста решить....сроки поджимают(
Заданы математическое ожидание m и среднее квадратичное отклонение q нормально распределненой,случайной велечины x.Найти: 1)вероятность того,что x примет значения,принадлежащие интервалу(альфа;бета)
2)вероятность того,что абсолютная величина отклонения!х-m!окажется меньше r
m=11 q=4 ((альфа)=17) ((бета)=26) r=12
|
Всего сообщений: 8 | Присоединился: январь 2009 | Отправлено: 16 окт. 2009 6:57 | IP
|
|
LIST

Новичок
|
    
Дайте совет по решению.
Средняя температура воздуха в июле в данной местности 20С. Оценить вероятность того, что в июле следующего года средняя температура воздуха будет: а) не более 15С; б) более 20С.
Может воспользоваться неравенствами Маркова?
Но тогда получаем следующее:
а) Х<=15, P(Х<=15)>=1-20/15=-0.33
Как это понять?
б) Х>20, P(Х>15)<=20/20=1
Как это понять?
|
Всего сообщений: 9 | Присоединился: октябрь 2009 | Отправлено: 16 окт. 2009 10:59 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: lokobum написал 15 окт. 2009 22:10
В первой урне 7 белых шаров и 3 черных,
во второй – 4 белых и 5 черных. Из первой
урны наугад вынули 2 шара и положили во
вторую. Какого цвета шар теперь более вероятно вынуть из второй урны?
H1 = {из первой урны достали два белых шарика}
H2 = {из первой урны достали белый и черный шары}
H3 = {из первой урны достали два черных шара}
P(H1) = C(2;7)/C(2;10) = 21/45 = 7/15
P(H2) = (7*3)/C(2;10) = 21/45 = 7/15
P(H3) = C(2;3)/C(2;10) = 3/45 = 1/15
A = {из второй урны вынули белый шар}
A|H1 = {из второй урны достали белый шар при условии, что из первой урны во вторую переложили два белых шара}
A|H2 = {из второй урны достали белый шар при условии, что из первой урны во вторую переложили белый и черный шары}
A|H3 = {из второй урны достали белый шар при условии, что из первой урны во вторую переложили два черных шара}
P(A|H1) = 6/11
P(A|H2) = 5/11
P(A|H3) = 4/11
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) + P(H3)P(A|H3) =
= (7/15)*(6/11) + (7/15)*(5/11) + (1/15)*(4/11) =
= 42/165 + 35/165 + 4/165 = 81/165 = 27/55
B = {из второй урны достали черный шар}
P(B) = 1 - P(A) = 1 - 27/55 = 28/55
P(A) < P(B)
Следовательно, более вероятно из второй урны достать черный шар
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 16 окт. 2009 11:05 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Sav написал 16 окт. 2009 6:57
Помогите пожалуйста решить....сроки поджимают(
Заданы математическое ожидание m и среднее квадратичное отклонение q нормально распределненой,случайной велечины x.Найти: 1)вероятность того,что x примет значения,принадлежащие интервалу(альфа;бета)
2)вероятность того,что абсолютная величина отклонения!х-m!окажется меньше r
m=11 q=4 ((альфа)=17) ((бета)=26) r=12

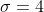



1)
 = P(17 < X < 26) = \Phi (\frac{26 - 11}{4}) - \Phi (\frac{17 - 11}{4}) = )
 - \Phi (1.5) \sim 0.499928 - 0.4332 = 0.066728 )
2)
 \sim 2\Phi (\frac{r}{\sigma}) = 2\Phi (\frac{12}{4}) = )
 \sim 2*(0.49865) = 0.9973 )
(Сообщение отредактировал RKI 16 окт. 2009 11:24)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 16 окт. 2009 11:19 | IP
|
|
natafka


Новичок
|
    
Помогите , пожалуйста ))))))
Производится 10 независимых опытов при одинаковых условиях; вероятность того, что в отдельном опыте погрешность превзойдет критическую величину, равна 0,2. Пусть случайная величина х - число опытов, в которых будет допущена такая погрешность. Найти математическое ожидание, дисперсию и наивероятнейшее значение х; найти вероятности того, что:
а) число неудачных опытов не превзойдет двух
б) хотя бы в одном опыте будет недопустимая погрешность
в) все опыты будут удачными.
|
Всего сообщений: 49 | Присоединился: ноябрь 2008 | Отправлено: 16 окт. 2009 11:33 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: natafka написал 16 окт. 2009 11:33
Помогите , пожалуйста ))))))
Производится 10 независимых опытов при одинаковых условиях; вероятность того, что в отдельном опыте погрешность превзойдет критическую величину, равна 0,2. Пусть случайная величина х - число опытов, в которых будет допущена такая погрешность. Найти математическое ожидание, дисперсию и наивероятнейшее значение х; найти вероятности того, что:
а) число неудачных опытов не превзойдет двух
б) хотя бы в одном опыте будет недопустимая погрешность
в) все опыты будут удачными.
Случайная величина X - число опытов с погрешностью.
n = 10 - количество независимых опытов
p = 0.2 - вероятность того, что опыт с погрешностью
q = 1 - p = 1 - 0.2 = 0.8
Случайная величина X имеет распределение Бернулли с параметрами n = 10 и p = 0.2. Следовательно,
M(X) = np = 10*(0.2) = 2
D(X) = npq = 10*(0.2)*(0.8) = 1.6
m* - наивероятнейшее значение, которое может принять случайная величина X
np - q <= m* <= np + p
10*(0.2) - 0.8 <= m* <= 10*(0.2) + 0.2
1.2 <= m* <= 2.2
m* = 2
а) P(X <= 2) = P(X=0) + P(X=1) + P(X=2) =
= (0.8)^10 + C(1;10)*(0.2)*((0.8)^9) +
+ C(2;10)*((0.2)^2)*((0.8)^8) =
= 0.1073741824 + 10*(0.2)*(0.134217728) +
+ 45*(0.04)*(0.16777216) =
= 0.1073741824 + 0.268435456 + 0.301989888 =
= 0.6777995264
б) P(X >= 1) = 1 - P(X < 1) = 1 - P(X=0) = 1 - (0.8)^10 =
= 1 - 0.1073741824 = 0.8926258176
в) P(X=0) = 0.1073741824
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 16 окт. 2009 12:45 | IP
|
|
Arhangel1990

Новичок
|
    
Помогите пожалуйста решить:
Случайная велечина Х задана функцией распределения F(x).Найти плотнось распределения вероятностей f(x),математическое ожидание M(x),дисперсию D(x),вероятность Р(0<x>0.5)
(Сообщение отредактировал Arhangel1990 16 окт. 2009 13:05)
|
Всего сообщений: 30 | Присоединился: июнь 2009 | Отправлено: 16 окт. 2009 13:03 | IP
|
|
lokobum


Новичок
|
       
спасибо большое прибольшое)) Выручили второй раз)
Всего всего вам хорошего, счастья, любви, успехов!
|
Всего сообщений: 5 | Присоединился: октябрь 2009 | Отправлено: 16 окт. 2009 13:08 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: vikycik написал 16 окт. 2009 2:18
20. Для доступа в компьютерную сеть оператору необходимо набрать пароль из 4 цифр. Оператор забыл или не знает необходимого кода. С какой вероятностью можно открыть замок с первой попытки?
Варианты ответов:
1)1/А(4;10)с чертой 2)1/А(4;10) 3)1/С(4;10) 4)1/С(4;10)с чертой 5)1/Р4
A = {замок можно открыть с первой попытки}
Посчитаем число n всевозможных исходов. Способов выбрать 4 цифры из 10 имеющихся (повтор возможен, порядок важен):
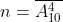
Посчитаем число m исходов, благоприятных событию A. Существует только один правильный пароль, то есть m=1.
По классическому определению вероятности
 = \frac{m}{n} = \frac{1}{\overline{A_{10}^{4} } } )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 16 окт. 2009 13:15 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: vikycik написал 16 окт. 2009 2:18
24. Какова вероятность, что дуэль состоится, если каждый из дуэлянтов приходит на место поединка в случайный момент времени между 5-ю и 6-ю часами и ждет противника в течение 5 минут?
Варианты ответов:
1)5/6 2)(5/6)^2 3)1-(5/6)^2 4)(11/12)^2 5)1-(11/12)^2
Пространство всевозможных исходов:
K = {(x;y): 5 <= x <= 6; 5 <= y <= 6}
S(K) = (6-5)*(6-5) = 1*1 = 1
A = {дуэль состоится}
A = {(x;y): 5 <= x <= 6; 5 <= y <= 6; |x-y| <= 1/12}
S(A) = 1 - (1/2)*(11/12)*(11/12) - (1/2)*(11/12)*(11/12) =
= 1 - (11/12)^2
По геометрическому определению вероятности
P(A) = S(A)/S(K) = 1 - (11/12)^2
27. В семье 6 детей. Найти вероятность того, что в данной семье не менее двух мальчиков, но не более четырех. Считать вероятности рождения мальчика и девочки равными 0,5.
Варианты ответов:
1) 0,219 2)0,781 3)0,344 4)0,656 5) 0,5
n = 6 - количество детей
p = 0.5 - вероятность того, что ребенок - мальчик
q = 1 - p = 1 - 0.5 = 0.5
m - количество мальчиков в семье
P(2 <= m <= 4) = P(m=2) + P(m=3) + P(m=4) =
= C(2;6)*((0.5)^2)*((0.5)^4) + C(3;6)*((0.5)^3)*((0.5)^3) +
+ C(4;6)*((0.5)^4)*((0.5)^2) =
= 15*(0.5)^6 + 20*(0.5)^6 + 15*(0.5)^6 =
= 50*(0.5)^6 =
= 0.78125
28. Вероятность того, что при 10 подбрасываниях симметричной монеты герб появится пять раз, равна:
Варианты ответов:
1)1/2 2)С(5;10) (1/2)^5 3)С(5;10) (1/2)^10 4)1/10! 5)1/4
n = 10 - количество подбрасываний
p = 1/2 - вероятность выпадения герба
q = 1 - p = 1 - 1/2 = 1/2
m - количество выпадений герба
P(m=5) = C(5;10)*((1/2)^5)*((1/2)^5) = C(5;10)*((1/2)^10)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 16 окт. 2009 13:24 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности