Lenusik


Новичок
|
    
помогите пожалуйста с задачками! не знаю как решать(
1.В первой урне 5 шаров – 2 белых и 3 черных. Во второй 3 шара – 1 белый и 2 черных. Из первой урны наудачу переложили во вторую 1 шар, после чего, из второй в первую переложили 1 шар. Случайная величина Х – число белых шаров в первой урне. Найти 1) ряд распределения случайной величины X; 2) функцию распределения; 3) математическое ожидание, дисперсию, среднеквадратическое отклонение, коэффициент асимметрии и эксцесс распределения.
2.Правильная монета подбрасывается трижды. Найти ковариацию числа орлов, выпавших при первых двух подбрасываниях монеты, и числа орлов, выпавших при всех трех подбрасываниях монеты.
3.Каждый из 240 абонентов АТС в любой момент времени может занимать линию с вероятностью 1/40. Каково минимальное число линий должна содержать АТС, чтобы вероятность потери вызова (занятости линии) не превосходила 0,005 (Использовать ЦПТ).
заранее спасибо!
|
Всего сообщений: 8 | Присоединился: ноябрь 2009 | Отправлено: 15 нояб. 2009 12:27 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Yulusik написал 15 нояб. 2009 8:25
2. Задана плотность распределения непрерывной случайной величины кси: f(x)=Acos(x) при х принадлежащем [-p/2;p/2];
f(x)=0 при х НЕ принадлежащем [-p/2;p/2]; Найти коэффициент А и функцию распределения F(x); построить графики f(x) и F(x); найти M(кси), D(кси), 6(кси), коэффициент асимметрии A(кси), эксцесс распределения Е(кси); найти вероятность попадания случайной величины в интервал
(-3;п/4).
8) эксцесс распределения
)^{4}) = M(X^{4}) = \int\limits_{-\infty}^{+\infty} x^{4}f(x)dx = )
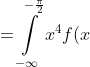dx + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } x^{4}f(x)dx + \int\limits_{\frac{\pi}{2} }^{+\infty} x^{4}f(x)dx = )
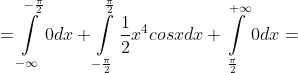
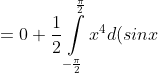 + 0 = )
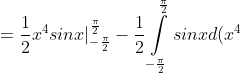 = )

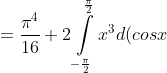 = )
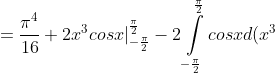 = )

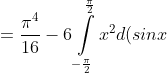 = )
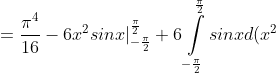 = )
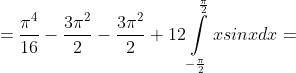
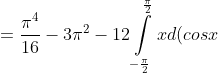 = )
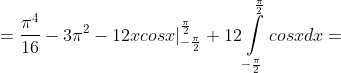


)^{4}) = \frac{\pi^{4} }{16} - 3\pi^{2} + 24 )
 = \frac{M((X - M(X))^{4})}{D^{2}(X)} - 3 = \frac{\frac{\pi^{4} }{16} - 3\pi^{2} + 24}{\frac{\pi^{4} - 16\pi^{2} + 64}{16} } - 3 = )

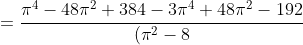^{2} } = )
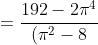^{2} } )
 = \frac{192 - 2\pi^{4} }{(\pi^{2} - 8)^{2} } )
(Сообщение отредактировал RKI 15 нояб. 2009 12:54)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 12:53 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Yulusik написал 15 нояб. 2009 8:25
3.Задана функция распределения непрерывной случайной величины кси:
F(x):{0 при х<=-2,
{Ax+B при -2<x<=4,
{1 при х>=4.
Найти: а)постоянные А и В; б)плотность вероятности f(x); в)
вероятность попадания случайной величины в интервал
[-3; 1], г) M(кси), D(кси). Построить графики f(x) и F(x)/
F(x) = {0, x <= -2
{Ax+B, -2 < x <= 4
{1, x > 4
а)
 = -2A + B = F(-2) = 0 )
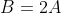
F(x) = {0, x <= -2
{Ax + 2A, -2 < x <= 4
{1, x > 4
 = 1 = F(4) = 4A + 2A = 6A )

F(x) = {0, x <= -2
{(1/6)x + 1/3, -2 < x <= 4
{1, x > 4
б) f(x) = F'(x)
f(x) = {0, x < -2
{1/6, -2 < x < 4
{0, x > 4
в) P(-3 <= X <= 1) = F(1) - F(-3) = (1/6 + 1/3) - 0 = 1/2
г) По виду плотности распределения можно утверждать, что случайная величина X имеет равномерное распределение на интервале (-2; 4).
Следовательно,
M(X) = (-2+4)/2 = 2/2 = 1.
D(X) = ((-2-4)^2)/12 = 36/12 = 3
(Сообщение отредактировал RKI 15 нояб. 2009 14:39)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 13:06 | IP
|
|
liza1

Новичок
|
     
RKI вот не могу разобраться в решении одной задачи на стр377
Для определения всхожести приготовленных для посева зёрен произведена выборка объемом 1000 штук. Опытным путем установили, что 80% зерен всхожи. Определить процент всхожих зерен во всей партии, если результат необходимо гарантировать с надёжностью 0.9
Вы нашли Доверительный интерва а вроде надо Определить процент всхожих зерен или это одно и тоже???????
|
Всего сообщений: 7 | Присоединился: ноябрь 2009 | Отправлено: 15 нояб. 2009 13:59 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: liza1 написал 15 нояб. 2009 13:59
Для определения всхожести приготовленных для посева зёрен произведена выборка объемом 1000 штук. Опытным путем установили, что 80% зерен всхожи. Определить процент всхожих зерен во всей партии, если результат необходимо гарантировать с надёжностью 0.9
Вы нашли Доверительный интерва а вроде надо Определить процент всхожих зерен или это одно и тоже???????
Извиняюсь, я неверно прочитала условие задачи
НЕт, это не одно и тоже
Это разные понятия
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 14:32 | IP
|
|
RKI 


Долгожитель
|
    
Drank
93 задача
p(x) = {0, x < 4
{1, 4 <= x <= 5
{0, x > 5

Найдем функцию распределения случайной величины Y.
 = P(Y < y) = P(\pi X^{2} < y) = P(X^{2} < \frac{y}{\pi}) )
Если y <= 0, то
 = P(X^{2} < \frac{y}{\pi}) = 0 )
Если y > 0, то
 = P(X^{2} < \frac{y}{\pi}) = P(-\frac{\sqrt{y} }{\sqrt{\pi} } < X < \frac{\sqrt{y} }{\sqrt{\pi} }) = )
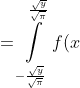dx )
Если y <= 16П, то
 = \int\limits_{-\frac{\sqrt{y} }{\sqrt{\pi} } }^{\frac{\sqrt{y} }{\sqrt{\pi} } } 0dx = 0 )
Если 16П < y <= 25П, то
 = \int\limits_{-\frac{\sqrt{y} }{\sqrt{\pi} } }^{\frac{\sqrt{y} }{\sqrt{\pi} } } f(x)dx = \int\limits_{-\frac{\sqrt{y} }{\sqrt{\pi} } }^{4} f(x)dx + \int\limits_{4}^{\frac{\sqrt{y} }{\sqrt{\pi} } } f(x)dx = )
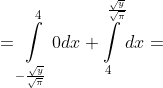
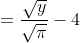
Если y > 25П, то
 = \int\limits_{-\frac{\sqrt{y} }{\sqrt{\pi} } }^{\frac{\sqrt{y} }{\sqrt{\pi} } } f(x)dx = )
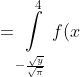dx + \int\limits_{4}^{5} f(x)dx + \int\limits_{5}^{\frac{\sqrt{y} }{\sqrt{\pi} } } f(x)dx = )
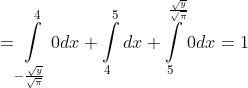
Функция распределения случайной величины Y имеет вид:
F(y) = {0, y <= 16П
{sqrt(y)/sqrt(П) - 4, 16П < y <= 25П
{1, y > 25П
p(y) = F'(y)
p(y) = {0, y < 16П
{1/2sqrt(Пy), 16П < y < 25П
{0, y > 25П
 = \int\limits_{-\infty}^{+\infty} yp(y)dy = \int\limits_{-\infty}^{16\pi} yp(y)dy + \int\limits_{16\pi}^{25\pi} yp(y)dy + \int\limits_{25\pi}^{+\infty} yp(y)dy = )

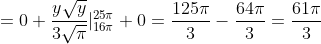
 = \int\limits_{-\infty}^{+\infty} y^{2}p(y)dy = \int\limits_{-\infty}^{16\pi} y^{2}p(y)dy + \int\limits_{16\pi}^{25\pi} y^{2}p(y)dy + \int\limits_{25\pi}^{+\infty} y^{2}p(y)dy = )
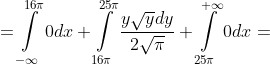
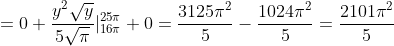
 = M(Y^{2}) - M^{2}(Y) = \frac{2101\pi^{2} }{5} - \frac{3721\pi^{2} }{9} = \frac{304\pi^{2} }{45} )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 15:39 | IP
|
|
RKI 


Долгожитель
|
    
Drank
94 задача
p(x) = {0, x < 4
{1, 4 <= x <= 5
{0, x > 5

 = \int\limits_{-\infty}^{+\infty} x^{2}p(x)dx = \int\limits_{-\infty}^{4} x^{2}p(x)dx + \int\limits_{4}^{5} x^{2}p(x)dx + \int\limits_{5}^{+\infty} x^{2}p(x)dx = )
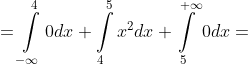

 = \frac{61}{3} )
 = M(2X^{2} + 1) = M(2X^{2}) + M(1) = 2M(X^{2}) + 1 = )

 = \frac{125}{3} )
 = \int\limits_{-\infty}^{+\infty} x^{4}p(x)dx = \int\limits_{-\infty}^{4} x^{4}p(x)dx + \int\limits_{4}^{5} x^{4}p(x)dx + \int\limits_{5}^{+\infty} x^{4}p(x)dx = )
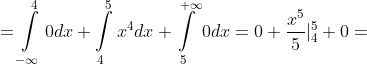

 = 420.2 )
 = M((2X^{2} + 1)^{2}) = M(4X^{4} + 4X^{2} + 1) = )
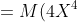 + M(4X^{2}) + M(1) = 4M(X^{4}) + 4M(X^{2}) + 1 = )

 = M(Y^{2}) - M^{2}(Y) = \frac{5289.4}{3} - \frac{15625}{9} = )
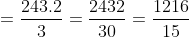
 = \frac{1216}{15} )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 16:21 | IP
|
|
maxman


Новичок
|
     
помогите чуток с задачами? Спасибо 
3.В лифт 9-этажного дома сели 5 пассажиров. Каждый независимо от других с одинаковой веро-ятностью может выйти на любом (начиная со второго) этаже. Определить вероятность того, что: а) все вышли на разных этажах; б) по крайней мере, трое сошли на одном этаже.
5.Моменты начала двух событий наудачу распределены в промежутке времени длиной 100 ми-нут. Одно из событий длится 10 мин., другое - 6 мин. Определить вероятность того, что: а) со-бытия «перекрываются» по времени; б) «не перекрываются».
9.Монета бросается до тех пор, пока орел не выпадает 4 раза. Определить вероятность того, что при этом решка выпадает 2 раза.
11.Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,03. Поступило 100 вызовов. Определить вероятность ровно 3 «сбоев».
12.Вероятность наступления некоторого события в каждом из 100 независимых испытаний равна 0,8. Определить вероятность того, что число m наступлений события удовлетворяет неравенству m <=(меньше или равно) 85.
(Сообщение отредактировал maxman 15 нояб. 2009 16:48)
|
Всего сообщений: 6 | Присоединился: ноябрь 2009 | Отправлено: 15 нояб. 2009 16:46 | IP
|
|
Yulusik

Новичок
|
     
RKI, спасибо огромного так выручил!!!!!!
|
Всего сообщений: 21 | Присоединился: сентябрь 2009 | Отправлено: 15 нояб. 2009 17:56 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Yulusik написал 15 нояб. 2009 17:56
RKI, спасибо огромного так выручил!!!!!!
Пожалуйста
Только я - это она 
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 18:25 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности