Форум - Решение задач по теории вероятности [378]

Форум	» Назад на решение задач по физике и термеху
Регистрация \| Профиль \| Войти \| Забытый пароль \| Присутствующие \| Справка \| Поиск

» Добро пожаловать, Гость: Войти | Регистрация

	Форум Математика Решение задач по теории вероятности
	Отметить все сообщения как прочитанные [ Помощь ] » Добро пожаловать на форум "Математика" «

Переход к теме
<< Назад Вперед >>

Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 235 236 237 238 239 240 241 242 243 244 245 246 247 248 249 250 251 252 253 254 255 256 257 258 259 260 261 262 263 264 265 266 267 268 269 270 271 272 273 274 275 276 277 278 279 280 281 282 283 284 285 286 287 288 289 290 291 292 293 294 295 296 297 298 299 300 301 302 303 304 305 306 307 308 309 310 311 312 313 314 315 316 317 318 319 320 321 322 323 324 325 326 327 328 329 330 331 332 333 334 335 336 337 338 339 340 341 342 343 344 345 346 347 348 349 350 351 352 353 354 355 356 357 358 359 360 361 362 363 364 365 366 367 368 369 370 371 372 373 374 375 376 377 378 379 380 381 382 383 384 385 386 387 388 389 390 391 392 393 394 395 396 397 398 399 400 ]
Модераторы: Roman Osipov, RKI, attention, paradise

RKI

Долгожитель

Цитата: shyrka написал 14 нояб. 2009 16:57

2) На вход электронного блока поступила кодовая комбинация, сформированная случайным образом из 0 и 1. Найти вероятность того, что эта комбинация содержит только одну единицу, а остальные нули. Всего знаков 4.

n = 4 - количество знаков

p = 1/2 - вероятность того, что на отдельной позиции стоит 1

q = 1 - p = 1 - 1/2 = 1/2

m - количество единиц

По формуле Бернулли
P(m=1) = C(1;4)*(1/2)*((1/2)^3) = 4*(1/2)*(1/8) = 1/4

(Сообщение отредактировал RKI 15 нояб. 2009 8:51)

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 8:50 | IP

RKI

Долгожитель

Цитата: Silent написал 14 нояб. 2009 19:02
1) Известны математическое ожидание m и среднее квадратическое отклонение q нормально распределённой случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (a, b). Изобразить на графике функции плотности найденную вероятность.
m=6, q=2, a=2, b=8.

$P(2 < X < 8) = \Phi (\frac{8 - 6}{2}) - \Phi (\frac{2 - 6}{2}) = \Phi (1) - \Phi (-2) =$

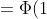$= \Phi (1) + \Phi (2) \sim 0.3413 + 0.4772 = 0.8185$

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 8:54 | IP

RKI

Долгожитель

Цитата: Silent написал 14 нояб. 2009 19:02

2) Событие происходит в первом опыте с вероятностью 0.2, во втором – 0.4, в третьем – 0.5. Построить распределение величины числа событий в трёх опытах. С какой вероятностью в трёх опытах возможно:
а) ровно одно событие;
б) хотя бы одно событие?
Если событие произошло ровно два раза, то с какой вероятностью оно не произошло в первом опыте, с какой – во втором и с какой – в третьем?

Случайная величина X - число событий в трех опытах. Данная случайная величина может принимать следующие значения: 0, 1, 2 или 3.

P(X=0) = (1 - 0.2)*(1 - 0.4)*(1 - 0.5) = (0.8)*(0.6)*(0.5) = 0.24

P(X=1) = (0.2)*(1 - 0.4)*(1 - 0.5) + (1 - 0.2)*(0.4)*(1 - 0.5) +
+ (1 - 0.2)*(1 - 0.4)*(0.5) =
= (0.2)*(0.6)*(0.5) + (0.8)*(0.4)*(0.5) + (0.8)*(0.6)*(0.5) =
= 0.06 + 0.16 + 0.24 = 0.46

P(X=2) = (0.2)*(0.4)*(1 - 0.5) + (0.2)*(1 - 0.4)*(0.5) +
+ (1 - 0.2)*(0.4)*(0.5) =
= (0.2)*(0.4)*(0.5) + (0.2)*(0.6)*(0.5) + (0.8)*(0.4)*(0.5) =
= 0.04 + 0.06 + 0.16 = 0.26

P(X=3) = (0.2)*(0.4)*(0.5) = 0.04

Закон распределения случайной величины X имеет вид
X 0 1 2 3
P 0.24 0.46 0.26 0.04

а) P(X=1) = 0.46
б) P(X >= 1) = 1 - P(X < 1) = 1 - P(X=0) = 1 - 0.24 = 0.76

A = {событие произошло 2 раза}
P(A) = P(X=2) = 0.26

Hi = {событие не произошло в i-том опыте} i = 1,2,3

AHi = {событие не произошло в i-том опыте и произошло в остальных двух опытах} i = 1,2,3
P(A|H1) = (1 - 0.2)*(0.4)*(0.5) = (0.8)*(0.4)*(0.5) = 0.16
P(A|H2) = (0.2)*(1 - 0.4)*(0.5) = (0.2)*(0.6)*(0.5) = 0.06
P(A|H3) = (0.2)*(0.4)*(1 - 0.5) = (0.2)*(0.4)*(0.5) = 0.04

Hi|A = {событие не произошло в i-том опыте при условии, что событие произошло в двух опытах} i=1,2,3

P(H1|A) = P(H1A)/P(A) = (0.16)/(0.26) = 16/26 = 8/13
P(H2|A) = P(H2A)/P(A) = (0.06)/(0.26) = 6/26 = 3/13
P(H3|A) = P(H3A)/P(A) = (0.04)/(0.26) = 4/26 = 2/13

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 9:08 | IP

Jorik

Новичок
Помогите,пожалуйста с задачами.
Из колоды в 52 карты вынимают 3 карты. Найти вероятость того, что:
а) среди вынутых будет хотя бы 1 туз
Я думаю,что решение такое:

б) появятся 6 бубей, 7 треф,10 пик
Я думаю,что решение такое:

На 10 карточка написаны бувы слова МАТЕМАТИКА.
А) Карточки перемешивают случ. образом и выбирают 5 карточек. Какова вероятность, что из отобранных карточек можно будет составить слово МЕТКА?
Мое решение:

Б) Найти вероятность того же события, если выбираются 6 карточек
Думаю,что так:

А вот эту задачу не могу вообще понять:
Подбрасываем 3 монеты. Найти:
а)вероятность P(k) того,что число выпавших гербов равно k(k=0,1,2,3)
б) вероятность того,что число выпавших гербюов более одного
в) вероятность того, что выпадет по крайней мере один герб

Смоежет проверить, правильно я решил, и подсказать последнюю задачу?

(Сообщение отредактировал Jorik 15 нояб. 2009 9:35)

Всего сообщений: 27 | Присоединился: февраль 2009 | Отправлено: 15 нояб. 2009 9:34 | IP

RKI

Долгожитель

Цитата: Yulusik написал 15 нояб. 2009 8:25

9. Случайная величина Х распределена равномерно на интервале (-п/2; п/2).Найти плотность распределения случайной величины Y=tg(X).

Плотность распределения случайной величины X имеет вид:
f(x) = {0, x <= -П/2
{1/П, -П/2 < x < П/2
{0, x >= П/2

Y = tgX

Построим функцию распределения случайной величины Y.

$F(y) = P(Y < y) = P(tgX < y) = P(X < arctgy) = \int\limits_{-\infty}^{arctgy} f(x)dx =$

$= \int\limits_{-\infty}^{-\frac{\pi}{2} } f(x)dx + \int\limits_{-\frac{\pi}{2} }^{arctgy} f(x)dx = \int\limits_{-\infty}^{-\frac{\pi}{2} } 0dx + \int\limits_{-\frac{\pi}{2} }^{arctgy} \frac{dx}{\pi} =$

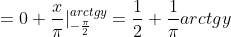
$= 0 + \frac{x}{\pi} |_{-\frac{\pi}{2} }^{arctgy} = \frac{1}{2} + \frac{1}{\pi}arctgy$

Функция распределения случайной величины Y имеет вид:
F(y) = 1/2 + (1/П)arctgy.

g(y) = F'(y)

Плотность распределения случайной величины Y имеет вид:
$g(y) = \frac{1}{\pi (1 + y^{2})}$

По виду плотности распределения случайной величины Y можно утверждать, что случайная величина Y имеет распределение Коши

(Сообщение отредактировал RKI 15 нояб. 2009 10:01)

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 10:00 | IP

shyrka

Новичок
Спасибо большое!!!!

Всего сообщений: 3 | Присоединился: ноябрь 2009 | Отправлено: 15 нояб. 2009 10:51 | IP

RKI

Долгожитель

Цитата: Yulusik написал 15 нояб. 2009 8:25

10. Случайная величина кси распределена равномерно на отрезке [-2;1]. Найти плотность распределения случайной величины n=1/(кси)^2.

Плотность распределения случайной величины X имеет вид:
f(x) = {0, x < -2
{1/3, -2 <= x <= 1
{0, x > 1

$Y = \frac{1}{X^{2} }$

Найдем функцию распределения случайной величины Y.

$F(y) = P(Y < y) = P(\frac{1}{X^{2} } < y)$

Если y <= 0, то
$F(y) = P(\frac{1}{X^{2} } < y) = 0$

Если y > 0, то
$F(y) = P(\frac{1}{X^{2} } < y) = P(X < -\frac{1}{\sqrt{y} }) + P(X > \frac{1}{\sqrt{y} }) =$

$= 1 - P(-\frac{1}{\sqrt{y} } \le X \le \frac{1}{\sqrt{y} }) = 1 - \int\limits_{-\frac{1}{\sqrt{y} } }^{\frac{1}{\sqrt{y} } } f(x)dx$

Если 0 < y <= 1/4, то
$F(y) = 1 - \int\limits_{-\frac{1}{\sqrt{y} } }^{\frac{1}{\sqrt{y} } } f(x)dx = 1 - \int\limits_{-\frac{1}{\sqrt{y} } }^{-2} f(x)dx - \int\limits_{-2}^{1} f(x)dx - \int\limits_{1}^{\frac{1}{\sqrt{y} } } f(x)dx =$

$= 1 - \int\limits_{-\frac{1}{\sqrt{y} } }^{-2} 0dx - \int\limits_{-2}^{1} \frac{dx}{3} - \int\limits_{1}^{\frac{1}{\sqrt{y} } } 0dx =$

$= 1 - 0 - \frac{x}{3} |_{-2}^{1} - 0 = 1 - 1 = 0$

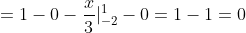
Если 1/4 < y <= 1, то
$F(y) = 1 - \int\limits_{-\frac{1}{\sqrt{y} } }^{\frac{1}{\sqrt{y} } } f(x)dx = 1 - \int\limits_{-\frac{1}{\sqrt{y} } }^{1} f(x)dx - \int\limits_{1}^{\frac{1}{\sqrt{y} } } f(x)dx =$

$= 1 - \int\limits_{-\frac{1}{\sqrt{y} } }^{1} \frac{dx}{3} - \int\limits_{1}^{\frac{1}{\sqrt{y} } } 0dx =$

$= 1 - \frac{x}{3} |_{-\frac{1}{\sqrt{y} } }^{1} - 0 = 1 - \frac{1}{3} - \frac{1}{3\sqrt{y} } = \frac{2}{3} - \frac{1}{3\sqrt{y} }$

Если y > 1, то
$F(y) = 1 - \int\limits_{-\frac{1}{\sqrt{y} } }^{\frac{1}{\sqrt{y} } } f(x)dx = 1 - \int\limits_{-\frac{1}{\sqrt{y} } }^{\frac{1}{\sqrt{y} } } \frac{dx}{3} =$

$= 1 - \frac{x}{3} |_{-\frac{1}{\sqrt{y} } }^{\frac{1}{\sqrt{y} } } = 1 - \frac{2}{3\sqrt{y} }$

Функция распределения случайной величины Y имеет вид:
F(y) = {0, y <= 1/4
{2/3 - 1/3sqrt(y), 1/4 < y <= 1
{1 - 2/3sqrt(y), y > 1

g(y) = F'(y)

Плотность распределения случайной величины Y имеет вид:
g(y) = {0, y < 1/4
{1/6ysqrt(y), 1/4 < y < 1
{1/3ysqrt(y), y > 1

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 11:18 | IP

RKI

Долгожитель

Цитата: Yulusik написал 15 нояб. 2009 8:25

2. Задана плотность распределения непрерывной случайной величины кси: f(x)=Acos(x) при х принадлежащем [-p/2;p/2];
f(x)=0 при х НЕ принадлежащем [-p/2;p/2]; Найти коэффициент А и функцию распределения F(x); построить графики f(x) и F(x); найти M(кси), D(кси), 6(кси), коэффициент асимметрии A(кси), эксцесс распределения Е(кси); найти вероятность попадания случайной величины в интервал
(-3;п/4).

f(x) = {0, x < -П/2
{Acosx, -П/2 <= x <= П/2
{0, x > П/2

1) коэффициент A

$1 = \int\limits_{-\infty}^{+\infty} f(x)dx = \int\limits_{-\infty}^{-\frac{\pi}{2} } f(x)dx + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } f(x)dx + \int\limits_{\frac{\pi}{2} }^{+\infty} f(x)dx =$

$= \int\limits_{-\infty}^{-\frac{\pi}{2} } 0dx + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } Acosxdx + \int\limits_{\frac{\pi}{2} }^{+\infty} 0dx =$

$= 0 + Asinx |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } + 0 = A + A = 2A$

$A = \frac{1}{2}$

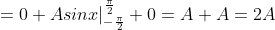
f(x) = {0, x < -П/2
{(1/2)cosx, -П/2 <= x <= П/2
{0, x > П/2
---------------------------------------------------------------------------------

2) Функция распределения

$F(x) = \int\limits_{-\infty}^{x} f(t)dt$

Если x <= -П/2, то
$F(x) = \int\limits_{-\infty}^{x} 0dt = 0$

Если -П/2 < x <= П/2, то
$F(x) = \int\limits_{-\infty}^{x} f(t)dt = \int\limits_{-\infty}^{-\frac{\pi}{2} } f(t)dt + \int\limits_{-\frac{\pi}{2} }^{x} f(t)dt =$

$= \int\limits_{-\infty}^{-\frac{\pi}{2} } 0dt + \int\limits_{-\frac{\pi}{2} }^{x} \frac{1}{2}costdt = 0 + \frac{1}{2}sint |_{-\frac{\pi}{2} }^{x} =$

$= \frac{1}{2} (sinx + 1)$

Если x > П/2, то
$F(x) = \int\limits_{-\infty}^{x} f(t)dt = \int\limits_{-\infty}^{-\frac{\pi}{2} } f(t)dt + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } f(t)dt + \int\limits_{\frac{\pi}{2} }^{x} f(t)dt =$

$= \int\limits_{-\infty}^{-\frac{\pi}{2} } 0dt + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } \frac{1}{2}costdt + \int\limits_{\frac{\pi}{2} }^{x} 0dt =$

$= 0 + \frac{1}{2}sint |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } + 0 = \frac{1}{2} (1 + 1) = 1$

F(x) = {0, x <= -П/2
{(1/2)(sinx + 1), -П/2 < x <= П/2
{1, x > П/2

--------------------------------------------------------------------------

3) математическое ожидание

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 11:48 | IP

RKI

Долгожитель

Цитата: Yulusik написал 15 нояб. 2009 8:25

2. Задана плотность распределения непрерывной случайной величины кси: f(x)=Acos(x) при х принадлежащем [-p/2;p/2];
f(x)=0 при х НЕ принадлежащем [-p/2;p/2]; Найти коэффициент А и функцию распределения F(x); построить графики f(x) и F(x); найти M(кси), D(кси), 6(кси), коэффициент асимметрии A(кси), эксцесс распределения Е(кси); найти вероятность попадания случайной величины в интервал
(-3;п/4).

3) математическое ожидание

$M(X) = \int\limits_{-\infty}^{+\infty} xf(x)dx = \int\limits_{-\infty}^{-\frac{\pi}{2} } xf(x)dx + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } xf(x)dx + \int\limits_{\frac{\pi}{2} }^{+\infty} xf(x)dx =$

$= \int\limits_{-\infty}^{-\frac{\pi}{2} } 0dx + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } \frac{1}{2}xcosxdx + \int\limits_{\frac{\pi}{2} }^{+\infty} 0dx =$

$= 0 + \frac{1}{2}\int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } xd(sinx) + 0 = \frac{1}{2}xsinx |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } - \frac{1}{2} \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } sinxdx =$

$= \frac{\pi}{4} - \frac{\pi}{4} + \frac{1}{2}cosx |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } = 0$

$M(X) = 0$

-------------------------------------------------------------------------

4) дисперсия

$M(X^{2}) = \int\limits_{-\infty}^{+\infty} x^{2}f(x)dx = \int\limits_{-\infty}^{-\frac{\pi}{2} } x^{2}f(x)dx + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } x^{2}f(x)dx + \int\limits_{\frac{\pi}{2} }^{+\infty} x^{2}f(x)dx =$

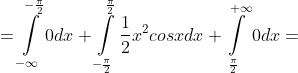
$= \int\limits_{-\infty}^{-\frac{\pi}{2} } 0dx + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } \frac{1}{2}x^{2}cosxdx + \int\limits_{\frac{\pi}{2} }^{+\infty} 0dx =$

$= 0 + \frac{1}{2}\int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } x^{2}d(sinx) + 0 = \frac{1}{2}x^{2}sinx |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } - \frac{1}{2}\int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } sinxd(x^{2}) =$

$= \frac{\pi^{2} }{8} + \frac{\pi^{2} }{8} - \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } xsinxdx = \frac{\pi^{2} }{4} + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } xd(cosx) =$

$= \frac{\pi^{2} }{4} + xcosx |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } - \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } cosxdx =$

$= \frac{\pi^{2} }{4} + 0 - 0 - sinx |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } = \frac{\pi^{2} }{4} - 1 - 1 =$

$= \frac{\pi^{2} }{4} - 2 = \frac{\pi^{2} - 8}{4}$

$M(X^{2}) = \frac{\pi^{2} - 8}{4}$

$D(X) = M(X^{2}) - M^{2}(X) = \frac{\pi^{2} - 8}{4} - 0 = \frac{\pi^{2} - 8}{4}$

---------------------------------------------------------------------------------

5) среднее квадратическое отклонение

$\sigma (X) = \sqrt{D(X)} = \frac{\sqrt{\pi^{2} - 8} }{2}$

-------------------------------------------------------------------------------

6) коэффициент асимметрии

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 12:08 | IP

RKI

Долгожитель

Цитата: Yulusik написал 15 нояб. 2009 8:25

2. Задана плотность распределения непрерывной случайной величины кси: f(x)=Acos(x) при х принадлежащем [-p/2;p/2];
f(x)=0 при х НЕ принадлежащем [-p/2;p/2]; Найти коэффициент А и функцию распределения F(x); построить графики f(x) и F(x); найти M(кси), D(кси), 6(кси), коэффициент асимметрии A(кси), эксцесс распределения Е(кси); найти вероятность попадания случайной величины в интервал
(-3;п/4).

6) коэффициент асимметрии

$M((X - M(X))^{3}) = M(X^{3}) = \int\limits_{-\infty}^{+\infty} x^{3}f(x)dx =$

$= \int\limits_{-\infty}^{-\frac{\pi}{2} } x^{3}f(x)dx + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } x^{3}f(x)dx + \int\limits_{\frac{\pi}{2} }^{+\infty} x^{3}f(x)dx =$

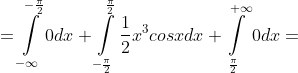
$= \int\limits_{-\infty}^{-\frac{\pi}{2} } 0dx + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } \frac{1}{2}x^{3}cosxdx + \int\limits_{\frac{\pi}{2} }^{+\infty} 0dx =$

$= 0 + \frac{1}{2} \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } x^{3}d(sinx) + 0 =$

$= \frac{1}{2}x^{3}sinx |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } - \frac{1}{2} \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } sinxd(x^{3}) =$

$= \frac{\pi^{3} }{16} - \frac{\pi^{3} }{16} - \frac{3}{2}\int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } x^{2}sinxdx =$

$= \frac{3}{2} \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } x^{2}d(cosx) = \frac{3}{2}x^{2}cosx |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } - \frac{3}{2} \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } cosxd(x^{2}) =$

$= - 3\int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } xcosxdx = - 3\int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } xd(sinx) =$

$= - 3xsinx |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } + 3\int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } sinxdx =$

$= - \frac{3\pi}{2} + \frac{3\pi}{2} - 3cosx |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } = - 0 + 0 = 0$

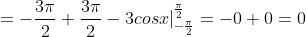
$M((X - M(X))^{3}) = 0$

$A(X) = \frac{M((X - M(X))^{3})}{\sigma^{3}(X)} = \frac{0}{\sigma^{3}(X)} = 0$

------------------------------------------------------------------------------

7) вероятность попадания

$P(-3 < X < \frac{\pi}{4}) = F(\frac{\pi}{4}) - F(-3) = \frac{1}{2}(sin\frac{\pi}{4} + 1) - 0 =$

$= \frac{1}{2}(\frac{\sqrt{2} }{2} + 1) = \frac{\sqrt{2} + 2}{4}$

------------------------------------------------------------------------------

8) эксцесс распределения

(Сообщение отредактировал RKI 15 нояб. 2009 12:27)

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 15 нояб. 2009 12:26 | IP