RKI 
Долгожитель
|
   
Цитата: liza1 написал 12 нояб. 2009 19:55
3
Для определения всхожести приготовленных для посева зёрен произведена выборка объемом 1000 штук. Опытным путем установили, что 80% зерен всхожи. Определить процент всхожих зерен во всей партии, если результат необходимо гарантировать с надёжностью 0.9
 = \frac{\gamma}{2} = 0.45 )
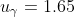
}{n} }u_{\gamma} < p < w + \sqrt{\frac{w(1-w)}{n} }u_{\gamma} )
77.91% < p < 82.09%
(Сообщение отредактировал RKI 13 нояб. 2009 20:05)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 20:04 | IP
|
|
liza1
Новичок
|
RKI и ещё раз огромное спасибо!!!!!
|
Всего сообщений: 7 | Присоединился: ноябрь 2009 | Отправлено: 13 нояб. 2009 21:14 | IP
|
|
Lenusik
Новичок
|
про меня чтото совсем забыли...(
|
Всего сообщений: 8 | Присоединился: ноябрь 2009 | Отправлено: 13 нояб. 2009 21:37 | IP
|
|
Cady
Новичок
|
спасибо большое-прибольшое! побольше таких добрых людей нам!!))
|
Всего сообщений: 6 | Присоединился: ноябрь 2009 | Отправлено: 13 нояб. 2009 21:51 | IP
|
|
tanyusya
Новичок
|
Здравствуйте!
Помогите пожалуйста решить вот такую задачку:
Плотность распределения непрерывной случайной величины Х имеет вид:
f(x) = (0 при -бесконечность<х<=3; а*(х-3) при 3<х<4; 0 при 4<=х<+бесконечность)
Найти:
а) параметр а
б) функцию распределения F(x)
в) вероятность попадания случайной величины Х в интервал (3,5 ; 5)
г) математическое ожидание и дисперсию
Построить графики функций F(x) b f(x).
Заранее большое спасибо.
|
Всего сообщений: 14 | Присоединился: июнь 2009 | Отправлено: 14 нояб. 2009 1:27 | IP
|
|
RKI
Долгожитель
|
Цитата: tanyusya написал 14 нояб. 2009 1:27
f(x) = (0 при -бесконечность<х<=3; а*(х-3) при 3<х<4; 0 при 4<=х<+бесконечность)
Найти:
а) параметр а
б) функцию распределения F(x)
в) вероятность попадания случайной величины Х в интервал (3,5 ; 5)
г) математическое ожидание и дисперсию
Построить графики функций F(x) b f(x).
f(x) = {0, x <= 3
{a(x-3), 3 < x < 4
{0, x >= 4
а)
dx = \int\limits_{-\infty}^{3} f(x)dx + \int\limits_{3}^{4} f(x)dx + \int\limits_{4}^{+\infty} f(x)dx = )
dx + \int\limits_{4}^{+\infty} 0dx = 0 + a\int\limits_{3}^{4} (x-3)dx + 0 = )
^{2} }{2} |_{3}^{4} = \frac{a}{2} )
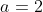
f(x) = {0, x <= 3
{2(x-3), 3 < x < 4
{0, x >= 4
б)
 = \int\limits_{-\infty}^{x} f(t)dt )
Если x <= 3, то
 = \int\limits_{-\infty}^{x} 0dt = 0 )
Если 3 < x <= 4, то
 = \int\limits_{-\infty}^{x} f(t)dt = \int\limits_{-\infty}^{3} f(t)dt + \int\limits_{3}^{x} f(t)dt = )
dt = 0 + (t-3)^{2} |_{3}^{x} = (x-3)^{2} )
Если x > 4, то
 = \int\limits_{-\infty}^{x} f(t)dt = \int\limits_{-\infty}^{3} f(t)dt + \int\limits_{3}^{4} f(t)dt + \int\limits_{4}^{x} f(t)dt = )
dt + \int\limits_{4}^{x} 0dt = 0 + (t-3)^{2} |_{3}^{4} + 0 = 1 )
F(x) = {0, x <= 3
{(x-3)^{2}, 3 < x <= 4
{1, x > 4
в) P(3.5 < X < 5) = F(5) - F(3.5) = 1 - (3.5 - 3)^2 =
= 1 - 0.25 = 0.75
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 14 нояб. 2009 11:32 | IP
|
|
Aleks123456789
Новичок
|
Помогите с задачей.
В бочке 2 шара, черный и белый.
Берут наугад один шар, затем кладут обратно и так повторяют 300 раз.
Какая вероятность вытащить хотя бы 1 раз хотя бы 4 черных шара подряд.
|
Всего сообщений: 1 | Присоединился: ноябрь 2009 | Отправлено: 14 нояб. 2009 13:35 | IP
|
|
ProstoVasya
Долгожитель
|
cough
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 14 нояб. 2009 13:41 | IP
|
|
Kuziaa
Новичок
|
Добрый день, помогите пожалуйста решить 2 задачи:
1. Дана плотность распределения f(x) случайной величины X. Найти параметр c, математическое ожидание M(X), дисперсию D(X), функцию распределения случайной величины X, вероятность выполнения неравенства 1.5<X<2.
a=1, b=2.4
2. Случайная велична X имеет плотность распределения вероятностей  . Найти плотность распределения вероятностей p(y) случайной величины  .
Заранее огромное спасибо!
|
Всего сообщений: 5 | Присоединился: октябрь 2009 | Отправлено: 14 нояб. 2009 14:20 | IP
|
|
liza1
Новичок
|
Пожалуйста спасайте!!!!
Очень срочно надо вот эти задачи!!!!
И заранее огромнейшее СПАСИБО!!!!
1.
Результаты измерения расстояния между двумя населёнными пунктами подчинены нормальному закону с параметрами а=16км b=100м Найти вероятность того, что расстояние между этими пунктами не менее 15,8 км.
2.
Для определения всхожести приготовленных для посева зёрен произведена выборка объемом 1000 штук. Опытным путем установили, что 80% зерен всхожи. Определить процент всхожих зерен во всей партии, если результат необходимо гарантировать с надёжностью 0.9
3.
Ниже приведены результаты выборочного обследования двух
партиё изделий
№ партии=1 Бракованные=8 Небракованные=92
№ партии=2 Бракованные=13 Небракованные=287
Можно ли считать, что доля брака в обеих партиях одна и та же? Уровень значимости принять равным 0.05.
(Сообщение отредактировал liza1 15 нояб. 2009 23:13)
|
Всего сообщений: 7 | Присоединился: ноябрь 2009 | Отправлено: 14 нояб. 2009 14:26 | IP
|
|
Форум
Решение задач по теории вероятности
