RKI 
Долгожитель
|
   
Цитата: Yulusik написал 13 нояб. 2009 12:21
8.Коробки с шоколадом упаковываются автоматически: их масса есть нормальная случайная величина со средним 1.06 кг. Найти среднеквадратическое отклонение случайной величины - массы коробок, если известно, что 5% коробок имеют массу меньше 1 кг.
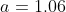
 = 0.05 )
 = 0.5 + \Phi (\frac{1 - 1.06}{\sigma}) = 0.5 + \Phi (-\frac{0.06}{\sigma}) = )
 = 0.05 )
 = 0.45 )
|
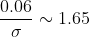
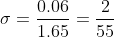
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 14:53 | IP
|
|
SVIRI
Новичок
|
ЕЩЕ ВОПРОС (3 COS 6X=0), ЧЕМУ РАВЕН Х
|
Всего сообщений: 8 | Присоединился: ноябрь 2009 | Отправлено: 13 нояб. 2009 15:14 | IP
|
|
RKI
Долгожитель
|
Цитата: maxman написал 12 нояб. 2009 20:33
1.В двух группах обучается по 25 студентов. В первой группе сессию на «отлично» сдали 7 че-ловек, во второй 4 человека. Из каждой группы наудачу вызывают по одному студенту. Какова вероятность того, что: а) оба студента отличники; б) только один отличник; в) хотя бы один отличник.
Ai = {из i-той группы вызвали отличника}, i=1,2
P(A1) = 7/25 = 0.28
P(A2) = 4/25 = 0.16
не Ai = {из i-той группы вызвали не отличника}, i=1,2
P(не A1) = 1 - P(A1) = 1 - 0.28 = 0.72
P(не A2) = 1 - P(A2) = 1 - 0.16 = 0.84
а) A = {оба студента отличники}
A = A1*A2
P(A) = P(A1*A2) = P(A1)*P(A2) = (0.28)*(0.16) = 0.0448
б) B = {только один отличник}
B = A1*(не A2) + (не A1)*A2
P(B) = P(A1*(не A2) + (не A1)*A2) =
= P(A1*(не A2)) + P((не A1)*A2) =
= P(A1)*P(не A2) + P(не A1)*P(A2) =
= (0.28)*(0.84) + (0.72)*(0.16) = 0.2352 + 0.1152 = 0.3504
в) C = {хотя бы один отличник}
не C = {ни одного отличника}
не C = (не A1)*(не A2)
P(не C) = P((не A1)*(не A2)) = P(не A1)*P(не A2) =
= (0.72)*(0.84) = 0.6048
P(C) = 1 - P(не C) = 1 - 0.6048 = 0.3952
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 16:19 | IP
|
|
RKI
Долгожитель
|
Цитата: maxman написал 12 нояб. 2009 20:33
2.Гардеробщица одновременно выдала номерки пяти лицам, сдавшим в гардероб свои шляпы, и повесила их наугад. Найти вероятность того, что она каждому выдаст его собственную шляпу.
A = {гардеробщица каждому выдаст его собственную шляпу}
Посчитаем число n всевозможных исходов. Способов разместить 5 шляп по 5 имеющимся местам:
n = 5! = 1*2*3*4*5 = 120.
Посчитаем число m исходов, благоприятных событию A. Разместить 5 шляп соответственно их номерам можно только одним способом:
m = 1.
По классическому определению вероятности
P(A) = m/n = 1/120.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 16:23 | IP
|
|
RKI
Долгожитель
|
Цитата: maxman написал 12 нояб. 2009 20:33
4.В отрезок единичной длины наудачу бросается 5 точек. Определить вероятность того, что две точки будут находиться от правого края отрезка на расстоянии меньшем 1/2, а три на расстоя-нии большем 1/2.
Посчитаем вероятность того, что одна отдельно взятая точка будет находится от правого края отрезка на расстоянии меньшем 1/2.
Пространство всевозможных исходов
O = {x: 0 <= x <= 1}.
l(O) = 1 - 0 = 1.
Пространство благоприятных исходов
A = {x: 1/2 < x <= 1}.
l(A) = 1 - 1/2 = 1/2
По геометрическому определению вероятности
P(A) = l(A)/l(O) = (1/2)/1 = 1/2
n = 5 - количество точек
p = P(A) = 1/2 - вероятность того, что точка будет от правого конца отрезка на расстоянии, меньшем 1/2
q = 1 - p = 1 - 1/2 = 1/2
m - количество точек, лежащих от правого конца отрезка на расстоянии, меньшем 1/2
По формуле Бернулли
P(m=2) = C(2;5)*((1/2)^2)*((1/2)^3) = 10/32 = 0.3125
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 16:48 | IP
|
|
RKI
Долгожитель
|
Цитата: maxman написал 12 нояб. 2009 20:33
6.Вероятность того, что цель поражена при одном выстреле первым стрелком – 0,61, вторым – 0,65. Первый сделал 2, второй - 3 выстрелов. Определить вероятность того, что цель не пора-жена.
Ai = {при i-том выстреле первый стрелок попал в мишень}, i=1,2
P(Ai) = 0.61
не Ai = {при i-том выстреле первый стрелок промахнулся}, i=1,2
P(не Ai) = 1 - P(Ai) = 1 - 0.61 = 0.39
Bi = {при i-том выстреле второй стрелок попал в мишень}, i=1,2,3
P(Bi) = 0.65
не Bi = {при i-Том выстреле второй стрелок промахнулся}, i=1,2,3
P(не Bi) = 1 - P(Bi) = 1 - 0.65 = 0.35
C = {цель не поражена}
C = (не A1)*(не A2)*(не B1)*(не B2)*(не B3)
P(C) = P((не A1)*(не A2)*(не B1)*(не B2)*(не B3)) =
= P(не A1)*P(не A2)*P(не B1)*P(не B2)*P(не B3) =
= (0.39)*(0.39)*(0.35)*(0.35)*(0.35) =
= 0.0065212875
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 16:59 | IP
|
|
RKI
Долгожитель
|
Цитата: maxman написал 12 нояб. 2009 20:33
7.В альбоме 8 чистых и 5 гашеных марок. Из них наудачу извлекаются 4 марки, подвергаются спецгашению и возвращаются в альбом. После этого вновь наудачу извлекается 4 марки. Оп-ределить вероятность того, что все они чистые.
H1 = {4 чистых марки}
H2 = {3 чистых и 1 гашеная марки}
H3 = {2 чистых и 2 гашеных марки}
H4 = {1 чистая и 3 гашеных марки}
H5 = {4 гашеных марки}
P(H1) = C(4;8)/C(4;13) = 70/715 = 14/143
P(H2) = C(3;8)C(1;5)/C(4;13) = 280/715 = 56/143
P(H3) = C(2;8)C(2;5)/C(4;13) = 280/715 = 56/143
P(H4) = C(1;8)C(3;5)/C(4;13) = 80/715 = 16/143
P(H5) = C(4;5)/C(4;13) = 5/715 = 1/143
A = {достали 4 чистые марки}
A|H1 = {достали 4 чистые марки, если в альбоме 4 чистых и 9 гашеных марок}
A|H2 = {достали 4 чистые марки, если в альбоме 5 чистых и 8 гашеных марок}
A|H3 = {достали 4 чистые марки, если в альбоме 6 чистых и 7 гашеных марок}
A|H4 = {достали 4 чистые марки, если в альбоме 7 чистых и 6 гашеных марок}
A|H5 = {достали 4 чистые марки, если в альбоме 8 чистых и 5 гашеных марок}
P(A|H1) = C(4;4)/C(4;13) = 1/715
P(A|H2) = C(4;5)/C(4;13) = 5/715
P(A|H3) = C(4;6)/C(4;13) = 15/715
P(A|H4) = C(4;7)/C(4;13) = 35/715
P(A|H5) = C(4;8)/C(4;13) = 70/715
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) + ... + P(H5)P(A|H5) =
= (14/143)*(1/715) + (56/143)*(5/715) + (56/143)*(15/715) + (16/143)*(35/715) + (1/143)*(70/715) =
= (14 + 280 + 840 + 560 + 70)/(143*715) = 1764/(143*715) =
= 1764/102245
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 17:20 | IP
|
|
RKI
Долгожитель
|
Цитата: maxman написал 12 нояб. 2009 20:33
8.Для проверки геодезических работ назначена группа экспертов, состоящая из трех подгрупп. В первой подгруппе - 2 человека, во второй - 5 и в третьей - 3. Эксперты первой подгруппы принимают верное решение с вероятностью 0,7, эксперты второй подгруппы c вероятностью 0,8, эксперты третьей подгруппы с вероятностью 0,6. Наудачу вызванный эксперт принимает 4 независимых решения. Найти вероятность того, что: а) ровно 3 решения приняты верно; б) принимал решения эксперт из первой подгруппы, если 3 решения приняты верно.
H1 = {эксперт из первой подгруппы}
H2 = {эксперт из второй подгруппы}
H3 = {эксперт из третьей подгруппы}
P(H1) = 2/(2+5+3) = 2/10 = 0.2
P(H2) = 5/10 = 0.5
P(H3) = 3/10 = 0.3
а) A = {ровно 3 решения приняты верно}
ِA|H1 = {3 решения приняты верно экспертом из первой группы}
A|H2 = {3 решения приняты верно экспертом из второй группы}
A|H3 = {3 решения приянты верно экспертом из третьей группы}
P(A|H1) = C(3;4)*((0.7)^3)*(0.3) = 0.4116
P(A|H2) = C(3;4)*((0.8)^3)*(0.2) = 0.4096
P(A|H3) = C(3;4)*((0.6)^3)*(0.4) = 0.3456
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) + P(H3)P(A|H3) =
= (0.2)*(0.4116) + (0.5)*(0.4096) + (0.3)*(0.3456) =
= 0.08232 + 0.2048 + 0.10368 = 0.3908
б) H1|A = {решения принимал эксперт из первой группы при условии, что 3 решения приняты верно}
По формуле Байеса
P(H1|A) = P(H1)P(A|H1)/P(A) = (0.08232)/(0.3908) =
= 1029/4885
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 18:41 | IP
|
|
RKI
Долгожитель
|
Цитата: maxman написал 12 нояб. 2009 20:33
10.На каждый лотерейный билет с вероятностью 0,1 может выпасть крупный выигрыш, с вероят-ностью 0,2 - мелкий выигрыш и с вероятностью 0,7 билет может оказаться без выигрыша. Куп-лено 15 билетов. Определить вероятность получения 1 крупного выигрыша и 2 мелких.
n = 15 - количество билетов
p1 = 0.1 - вероятность крупного выигрыша
p2 = 0.2 - вероятность мелкого выигрыша
p3 = 0.7 - вероятность проигрыша
p1 + p2 + p3 = 0.1 + 0.2 + 0.7 = 1
m1 - количество билетов с крупным выигрышем
m2 - количество билетов с мелким выигрышем
m3 - количество билетов с проигрышем
m1 + m2 + m3 = n = 15
По полиномиальной схеме
P(m1 = 1, m2 = 2, m3 = 12) =
= 15!/1!2!12! * (0.1)*((0.2)^2)*((0.7)^12) =
= 0.07557342811746
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 18:50 | IP
|
|
cough
Новичок
|
 
помогите, пожалуйста, с идз.
1.Время работы элемента до отказа подчинено показательному закону распределения с параметром альфа = 2*(10^(-5)) ч^(-1). Найти среднее время между появлением двух смежных отказов и вероятность безотказной работы к моменту среднего времени после включения технического устройства.
2. Случайная величина b распределена равномерно на отрезке [-2;1] . Найти плотность распределения случайной величины b= 1/ E^2.
3.Пусть e и n — независимые случайные величины, причем имеет равномерное на отрезке [–1, 1] распределение, а n имеет биномиальное распределение с параметрами 2 и 1/2. Найти функцию и плотность распределения суммы e+n.
4.Складывается 10^4 чисел, каждое из которых округлено с точностью до 10^(-m) . Предполагается, что ошибки от округления независимы и равномерно распределены в интервале (- 0.5*(10^(-m)), 0.5*(10^(-m))). Используя центральную предельную теорему найти пределы, в которых с вероятностью 0,99, будет лежать суммарная ошибка.
5. Случайная величина e является средней арифметической независимых и одинаково распределенных случайных величин, среднеквадратическое отклонение каждой из которых равно 2. Сколько нужно взять таких величин, чтобы случайная величина e с вероятностью, не меньшей 0,92, имела отклонение от своего математического ожидания, не превосходящее 0,05. Решить задачу, используя а) неравенство Чебышева; б) центральную предельную теорему.
|
Всего сообщений: 4 | Присоединился: ноябрь 2009 | Отправлено: 13 нояб. 2009 19:41 | IP
|
|
|
Форум
Решение задач по теории вероятности
