RKI 
Долгожитель
|
   
Цитата: liza1 написал 12 нояб. 2009 19:55
2.
Дана плотность f(х) распределения случайной величины X. Требуется найти:
А) неизвестный параметр с;
Б)функцию распределения случайной величины Х; В)вероятность Р(а<=Х<=b) того, что случайная величина X примет значение из интервала [а,b);
Г) математическое ожидание случайной величины X.
Дано
а=0,b=1
f(х)=2с/1+х^2
х=(-Бесконечность;+бесконечность)
 = \frac{2c}{1+x^{2} } )
а)
dx = \int\limits_{-\infty}^{+\infty} \frac{2cdx}{1 + x^{2} } = )
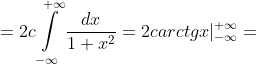
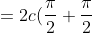 = 2\pi c = 1 )
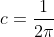
 = \frac{1}{\pi (1 + x^{2})} )
б)
 = \int\limits_{-\infty}^{x} f(t)dt = \int\limits_{-\infty}^{x} \frac{dt}{\pi (1 + t^{2})} = )
 = )
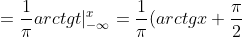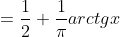
 = \frac{1}{2} + \frac{1}{\pi} arctgx )
в)
 = F(1) - F(0) = \frac{1}{2} + \frac{1}{\pi}arctg1 - \frac{1}{2} - \frac{1}{\pi} arctg0 = )
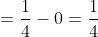
г)
 = \int\limits_{-\infty}^{+\infty} xf(x)dx = \int\limits_{-\infty}^{+\infty} \frac{xdx}{\pi (1 + x^{2})} = )
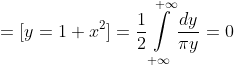
 = 0 )
(Сообщение отредактировал RKI 13 нояб. 2009 12:48)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 12:47 | IP
|
|
RKI
Долгожитель
|
Цитата: Yulusik написал 13 нояб. 2009 12:21
1.Имеется 5 ключей, из которых только один подходит к замку. Случайная величина Х - число проб при открывании замка (испробованный ключ в последующих пробах не участвует). Найти 1) ряд распределения случайной величины X; 2) функцию распределения; 3) математическое ожидание, дисперсию, среднеквадратическое отклонение, коэффициент асимметрии и эксцесс распределения.
Случайная величина X - число испробованных ключей. Данная случайная величина может принимать следующие значения:1, 2, 3, 4, 5.
Событие {X=k} означает, что k-1 ключей не подходили к замку, а k ключ подошел.
P(X=1) = 1/5
P(X=2) = (4/5)*(1/4) = 1/5
P(X=3) = (4/5)*(3/4)*(1/3) = 1/5
P(X=4) = (4/5)*(3/4)*(2/3)*(1/2) = 1/5
P(X=5) = (4/5)*(3/4)*(2/3)*(1/2)*(1/1) = 1/5
Ряд распределения случайной величины X имеет вид:
X 1 2 3 4 5
P 1/5 1/5 1/5 1/5 1/5
Функция распределения случайной величины X имеет вид:
F(x) = {0, x <= 1
{1/5, 1 < x <= 2
{2/5, 2 < x <= 3
{3/5, 3 < x <= 4
{4/5, 4 < x <= 5
{1, x > 5
M(X) = 1*(1/5) + 2*(1/5) + 3*(1/5) + 4*(1/5) + 5*(1/5) =
= (1/5)*(1 + 2 + 3 + 4 + 5) = 15/5 = 3
Математическое ожидание: M(X) = 3
M(X^2) = 1*(1/5) + 4*(1/5) + 9*(1/5) + 16*(1/5) + 25*(1/5) =
= (1/5)*(1 + 4 + 9 + 16 + 25) = 55/5 = 11
D(X) = M(X^2) - (M(X))^2 = 11 - 9 = 2
Дисперсия: D(X) = 2
б(X) = sqrt(D(X)) = sqrt(2) ~ 1.4142
Среднее квадратическое отклонение: б(X) = sqrt(2).
M(X^3) = 1*(1/5) + 8*(1/5) + 27*(1/5) + 64*(1/5) + 125*(1/5) =
= (1/5)*(1 + 8 + 27 + 64 + 125) = 225/5 = 45
M((X - M(X))^3) = M((X - 3)^3) = M(X^3 - 9X^2 + 27X - 27) =
= M(X^3) - M(9X^2) + M(27X) - M(27) =
= M(X^3) - 9M(X^2) + 27M(X) - 27 =
= 45 - 9*11 + 27*3 - 27 = 45 - 99 + 81 - 27 = 0
Коэффициент асимметрии: M((X - M(X))^3)/(б^3) = 0.
M(X^4) = 1*(1/5) + 16*(1/5) + 81*(1/5) + 256*(1/5) + 625*(1/5) =
= (1/5)*(1 + 16 + 81 + 256 + 625) = 979/5 = 195.8
M((X - M(X))^4) = M((X - 3)^4) =
= M(X^4 - 12X^3 + 18X^2 + 108X + 81) =
= M(X^4) - M(12X^3) + M(18X^2) + M(108X) + M(81) =
= M(X^4) - 12M(X^3) + 18M(X^2) + 108M(X) + 81 =
= 195.8 - 12*45 + 18*11 + 108*3 + 81 =
= 195.8 - 540 + 198 + 324 + 81 = 258.8
Коэффициент эксцесса: M((X - M(X))^4)/(D(X))^2 - 3 = (258.8)/4 - 3 = 61.7
(Сообщение отредактировал RKI 13 нояб. 2009 14:05)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 13:45 | IP
|
|
SVIRI
Новичок
|
RKI ПОМОГИТЕ ОСТАЛАСЬ ПОСЛЕДНЯЯ ЗАДАЧА, НЕ МОГУ РЕШИТЬ, ХОТЯ БЫ КАК СОСТАВИТЬ РЯД РАСПРЕДЕЛЕНИЯ. ВСЕ ОСТАЛЬНОЕ РЕШУ САМА. СРОЧНО НАДО ПОЖАЛУЙСТА
|
Всего сообщений: 8 | Присоединился: ноябрь 2009 | Отправлено: 13 нояб. 2009 13:58 | IP
|
|
RKI
Долгожитель
|
Цитата: SVIRI написал 13 нояб. 2009 13:58
RKI ПОМОГИТЕ ОСТАЛАСЬ ПОСЛЕДНЯЯ ЗАДАЧА, НЕ МОГУ РЕШИТЬ, ХОТЯ БЫ КАК СОСТАВИТЬ РЯД РАСПРЕДЕЛЕНИЯ. ВСЕ ОСТАЛЬНОЕ РЕШУ САМА. СРОЧНО НАДО ПОЖАЛУЙСТА
через 5 минут отправлю решение
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 14:07 | IP
|
|
RKI
Долгожитель
|
Цитата: SVIRI написал 13 нояб. 2009 11:56
RKI помогите решить задачу.
трое квалифицированных рабочих обратились за помощью в поисках работы в службу занятости. Вероятность того, что каждый из них в течение месяца получит подходящую работу соответственно равно 0,5;0,6;0,7. Составить ряд распределения числа рабочих , получивших работу в течении месяца. Найти M(x),D(x), среднее квадратическое отклонение числа таких рабочих, построить функцию распределения
Случайная величина X - число рабочих, получивших работу в течение месяца. Данная случайная величина может принимать следующие значения: 0, 1, 2 или 3.
P(X=0) = (1-0.5)*(1-0.6)*(1-0.7) = (0.5)*(0.4)*(0.3) = 0.06
P(X=1) = (0.5)*(1-0.6)*(1-0.7) + (1-0.5)*(0.6)*(1-0.7) + (1-0.5)*(1-0.6)*(0.7) =
= (0.5)*(0.4)*(0.3) + (0.5)*(0.6)*(0.3) + (0.5)*(0.4)*(0.7) =
= 0.06 + 0.09 + 0.14 = 0.29
P(X=2) = (0.5)*(0.6)*(1-0.7) + (0.5)*(1-0.6)*(0.7) + (1-0.5)*(0.6)*(0.7) =
= (0.5)*(0.6)*(0.3) + (0.5)*(0.4)*(0.7) + (0.5)*(0.6)*(0.7) =
= 0.09 + 0.14 + 0.21 = 0.44
P(X=3) = (0.5)*(0.6)*(0.7) = 0.21
Ряд распределения случайной величины X имеет вид:
X 0 1 2 3
P 0.06 0.29 0.44 0.21
Функция распределения случайной величины X имеет вид:
F(x) = {0, x <= 0
{0.06, 0 < x <= 1
{0.35, 1 < x <= 2
{0.79, 2 < x <= 3
{1, x > 3
M(X) = 0*(0.06) + 1*(0.29) + 2*(0.44) + 3*(0.21) =
= 0.29 + 0.88 + 0.63 = 1.8
M(X^2) = 0*(0.06) + 1*(0.29) + 4*(0.44) + 9*(0.21) =
= 0.29 + 1.76 + 1.89 = 3.94
D(X) = M(X^2) - (M(X))^2 = 3.94 - 3.24 = 0.7
б(X) = sqrt(D(X)) = sqrt(0.7) ~ 0.8367
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 14:17 | IP
|
|
SVIRI
Новичок
|
СПАСИБО БУДУ ПРИ МНОГО БЛАГОДАРНА
|
Всего сообщений: 8 | Присоединился: ноябрь 2009 | Отправлено: 13 нояб. 2009 14:18 | IP
|
|
RKI
Долгожитель
|
Цитата: SVIRI написал 13 нояб. 2009 14:18
СПАСИБО БУДУ ПРИ МНОГО БЛАГОДАРНА
Смотрите выше
Решение уже выложено
Пожалуйста
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 14:23 | IP
|
|
SVIRI
Новичок
|
RKI СПАСИБО.
|
Всего сообщений: 8 | Присоединился: ноябрь 2009 | Отправлено: 13 нояб. 2009 14:33 | IP
|
|
RKI
Долгожитель
|
Цитата: Yulusik написал 13 нояб. 2009 12:21
4.Случайная величина может принимать два значения: 2 и –2 с равной вероятностью. Найти характеристическую функцию случайной величины g(t) и, используя ее, вычислить математическое ожидание и дисперсию случайной величины X .
X -2 2
P 1/2 1/2
 = \frac{1}{2}e^{-2it} + \frac{1}{2}e^{2it} = \frac{1}{2}(e^{2it} + e^{-2it}) )
 = \frac{1}{2}(2ie^{2it} - 2ie^{-2it}) = i(e^{2it} - e^{-2it}) )
 = i(e^{0} - e^{0}) = i(1 - 1) = 0 )
 = g'(0) = 0 )
 = \frac{0}{i} = 0 )
 = i(2ie^{2it} + 2ie^{-2it}) = 2i^{2} (e^{2it} + e^{-2it}) = - 2(e^{2it} + e^{-2it}) )
 = - 2(e^{0} + e^{0}) = -2(1+1) = -4 )
 = g''(0) = -4 )
 = \frac{-4}{i^{2} } = \frac{-4}{-1} = 4 )
 = M(X^{2}) - M^{2}(X) = 4 - 0 = 4 )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 13 нояб. 2009 14:37 | IP
|
|
liza1
Новичок
|
RKI огромное спасибо!!!!
(Сообщение отредактировал liza1 13 нояб. 2009 21:25)
|
Всего сообщений: 7 | Присоединился: ноябрь 2009 | Отправлено: 13 нояб. 2009 14:46 | IP
|
|
|
Форум
Решение задач по теории вероятности
