otan27
Новичок
|
   
Ещё 2 задачи нерешёные, нужна помощь:
1.Баскетболист делает по кольцу 2 трёхочковых и 3 двухочковых броска. Составить закон распределения и найти сигма(X) для случайной величины Х - числа набранных баскетболистом очков, если вероятность попадания двухочкового и трёхочкового броска равны 0,7 и 0,4 соответственно.
2.Имеется n урн, в каждой из которых по m белых и по k черных шаров. Из первой урны наудачу извлекается один шар и перекладывается во вторую. Затем из второй урны наудачу извлекается один шар и перекладывается в третью урну и т.д. Определить вероятность извлечения после такого перекладывания белого шара из белой урны.
|
Всего сообщений: 9 | Присоединился: ноябрь 2009 | Отправлено: 12 нояб. 2009 11:08 | IP
|
|
RKI 
Долгожитель
|
Цитата: otan27 написал 12 нояб. 2009 11:08
1.Баскетболист делает по кольцу 2 трёхочковых и 3 двухочковых броска. Составить закон распределения и найти сигма(X) для случайной величины Х - числа набранных баскетболистом очков, если вероятность попадания двухочкового и трёхочкового броска равны 0,7 и 0,4 соответственно.
Случайная величина X - число набранных баскетболистом очков. Данная случайная величина может принимать следующие значения:
{X=0} - пять промахов
{X=2} - одно попадание в 2 очка
{X=3} - одно попадание в 3 очка
{X=4} - два попадания по 2 очка
{X=5} - одно попадание в 2 очка и одно попадание в 3 очка
{X=6} - два попадания в 3 очка ИЛИ три попадания в 2 очка
{X=7} - одно попадание в 3 очка и два попадания в 2 очка
{X=8} - два попадания в 3 очка и одно попадание в 2 очка
{X=9} - одно попадание в 3 очка и три попадания в 2 очка
{X=10} - два попадания в 3 очка и два попадания в 2 очка
{X=12} - все пять попаданий
n1 = 2 - количество бросков в 3 очка
p1 = 0.4 - вероятность попадания в 3 очка
q1 = 1 - p1 = 1 - 0.4 = 0.6
m1 - количество попаданий в 3 очка
n2 = 3 - количество бросков в 2 очка
p2 = 0.7 - вероятность попадания в 2 очка
q2 = 1 - p2 = 1 - 0.7 = 0.3
m2 - количество попаданий в 2 очка
P(X=0) = P(m1=0, m2=0) = P(m1=0)P(m2=0) =
= ((0.6)^2)*((0.3)^3) = 0.00972
P(X=2) = P(m1=0, m2=1) = P(m1=0)P(m2=1) =
= ((0.6)^2)*C(1;3)*(0.7)*((0.3)^2) = 0.06804
P(X=3) = P(m1=1,m2=0) = P(m1=1)P(m2=0) =
= C(1;2)*(0.6)*(0.4)*((0.3)^3) = 0.01296
P(X=4) = P(m1=0,m2=2) = P(m1=0)P(m2=2) =
= ((0.6)^2)*C(2;3)*((0.7)^2)*(0.3) = 0.15876
P(X=5) = P(m1=1,m2=1) = P(m1=1)P(m2=1) =
= C(1;2)*(0.6)*(0.4)*C(1;3)*(0.7)*((0.3)^2) = 0.09072
P(X=6) = P(m1=2,m2=0) + P(m1=0,m2=3) =
= P(m1=2)P(m2=0) + P(m1=0)P(m2=3) =
= ((0.4)^2)*((0.3)^3) + ((0.6)^2)*((0.7)^3) =
= 0.00432 + 0.12348 = 0.1278
P(X=7) = P(m1=1,m2=2) = P(m1=1)P(m2=2) =
= C(1;2)*(0.4)*(0.6)*C(2;3)*((0.7)^2)*(0.3) = 0.21168
P(X=8) = P(m1=2,m2=1) = P(m1=2)P(m2=1) =
= ((0.4)^2)*C(1;3)*(0.7)*((0.3)^2) = 0.03024
P(X=9) = P(m1=1,m2=3) = P(m1=1)P(m2=3) =
= C(1;2)*(0.6)*(0.4)*((0.7)^3) = 0.16464
P(X=10) = P(m1=2,m2=2) = P(m1=2)P(m2=2) =
= ((0.4)^2)*C(2;3)*((0.7)^2)*(0.3) = 0.07056
P(X=12) = P(m1=2,m2=3) = P(m1=2)P(m2=3) =
= ((0.4)^2)*((0.7)^3) = 0.05488
Закон распределения случайной величины X имеет вид:
X 0 2 3 4 5 6
P 0.00972 0.06804 0.01296 0.15876 0.09072 0.1278
X 7 8 9 10 12
P 0.21168 0.03024 0.16464 0.07056 0.05488
M(X) = 0*(0.00972) + 2*(0.06804) + 3*(0.01296) +
+ 4*(0.15876) + 5*(0.09072) + 6*(0.1278) +
+ 7*(0.21168) + 8*(0.03024) + 9*(0.16464) +
+ 10*(0.07056) + 12*(0.05488) =
= 0.13608 + 0.03888 + 0.63504 + 0.4536 + 0.7668 +
+ 1.48176 + 0.24192 + 1.48176 + 0.7056 + 0.65856 =
= 6.6
M(X^2) = 0*(0.00972) + 4*(0.06804) + 9*(0.01296) +
+ 16*(0.15876) + 25*(0.09072) + 36*(0.1278) +
+ 49*(0.21168) + 64*(0.03024) + 81*(0.16464) +
+ 100*(0.07056) + 144*(0.05488) =
= 0.27216 + 0.11664 + 2.54016 + 2.268 + 4.6008 +
+ 10.37232 + 1.93536 + 13.33584 + 7.056 + 7.90272 =
= 50.4
D(X) = M(X^2) - (M(X))^2 = 50.4 - 43.56 = 6.84
б(X) = sqrt(D(X)) = sqrt(6.84) ~ 2.6153...
(Сообщение отредактировал RKI 12 нояб. 2009 14:41)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 нояб. 2009 14:20 | IP
|
|
lapo4ka888
Новичок
|
помогите пожалуйста:
При участии в числовой лотерее в карточке отмечается 6 чисел(номеров) из числа возможных,равном 18.Число выигрышных номеров-случайная величина Х
1)составить ряд распределения этой случайной величины
2)Найти функцию распределения и построить её график
3)Найти математическое ожидание,дисперсию и среднеквадратическое отклонение этого распределения
4)Определить коэф-т асимметрии
заранеее спасибо
|
Всего сообщений: 2 | Присоединился: ноябрь 2009 | Отправлено: 12 нояб. 2009 14:37 | IP
|
|
SvetYulya
Новичок
|
Здравстуйте,RKI !!Мы снова к Вам за помощью!Не откажите пожалуйста!
1. При последовательных независимых испытаниях трех приборов на надежность каждый следующий прибор испытывается в том случае, если предыдущий оказался надежным. Определить математическое ожидание и дисперсию случайного числа испытанных приборов,если вероятность надежности прибора равна 0,6.
2. Случайная величина X задана функцией распределения:
F(x) = {0, x < 0
{(2arcsin x)/Пи, 0 <= x <= 1
{1, х>1
Найти: плотность вероятности f(x), вероятность попадания случайной величины в интервал (0;1/2) среднеквадратическое отклонение X.
3.Случайная величина X задана функцией распределения:
F(x) = {ln x, 1<x<e
{0, x<=1
{1, x>=e
Найти: плотность вероятности f(x),вероятность попадания случайной величины в интервал(1;2), среднеквадратическое отклонение X.
Заранее большое спасибо!
|
Всего сообщений: 11 | Присоединился: ноябрь 2009 | Отправлено: 12 нояб. 2009 14:47 | IP
|
|
RKI
Долгожитель
|
Цитата: SvetYulya написал 12 нояб. 2009 14:47
1. При последовательных независимых испытаниях трех приборов на надежность каждый следующий прибор испытывается в том случае, если предыдущий оказался надежным. Определить математическое ожидание и дисперсию случайного числа испытанных приборов,если вероятность надежности прибора равна 0,6.
Случайная величина X - число испытанных приборов. Данная случайная величина может принимать следующие значения:
{X=1} - первый испытанный прибор оказался ненадежным
{X=2} - первый прибор оказался надежным, а второй - нет
{X=3} - первые два прибора оказались надежными
P(X=1) = 0.4
P(X=2) = (0.6)*(0.4) = 0.24
P(X=3) = (0.6)*(0.6) = 0.36
Закон распределения случайной величины X имеет вид:
X 1 2 3
P 0.4 0.24 0.36
M(X) = 1*(0.4) + 2*(0.24) + 3*(0.36) =
= 0.4 + 0.48 + 1.08 = 1.96
M(X) = 1.96 - математическое ожидание
M(X^2) = 1*(0.4) + 4*(0.24) + 9*(0.36) =
= 0.4 + 0.96 + 3.24 = 4.6
D(X) = M(X^2) - (M(X))^2 = 4.6 - 3.8416 = 0.7584
D(X) = 0.7584 - дисперсия
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 нояб. 2009 15:07 | IP
|
|
Lenusik
Новичок
|
и я снова за помощью! помогите пожалуйста!
1.В первой урне 5 шаров – 2 белых и 3 черных. Во второй 3 шара – 1 белый и 2 черных. Из первой урны наудачу переложили во вторую 1 шар, после чего, из второй в первую переложили 1 шар. Случайная величина Х – число белых шаров в первой урне. Найти 1) ряд распределения случайной величины X; 2) функцию распределения; 3) математическое ожидание, дисперсию, среднеквадратическое отклонение, коэффициент асимметрии и эксцесс распределения.
2.Правильная монета подбрасывается трижды. Найти ковариацию числа орлов, выпавших при первых двух подбрасываниях монеты, и числа орлов, выпавших при всех трех подбрасываниях монеты.
3.Каждый из 240 абонентов АТС в любой момент времени может занимать линию с вероятностью 1/40. Каково минимальное число линий должна содержать АТС, чтобы вероятность потери вызова (занятости линии) не превосходила 0,005 (Использовать ЦПТ).
заранее благодарю!)
|
Всего сообщений: 8 | Присоединился: ноябрь 2009 | Отправлено: 12 нояб. 2009 15:09 | IP
|
|
RKI
Долгожитель
|
Цитата: SvetYulya написал 12 нояб. 2009 14:47
2. Случайная величина X задана функцией распределения:
F(x) = {0, x < 0
{(2arcsin x)/Пи, 0 <= x <= 1
{1, х>1
Найти: плотность вероятности f(x), вероятность попадания случайной величины в интервал (0;1/2) среднеквадратическое отклонение X.
F(x) = {0, x < 0
{2arcsinx/П, 0 <= x <= 1
{1, x > 1
f(x) = F'(x)
f(x) = {0, x < 0
{2/Пsqrt(1 - x^2), 0 < x < 1
{0, x > 1
P(0 < X < 1/2) = F(1/2) - F(0) = 2arcsin(1/2)/П - 2arcsin0/П =
= 2(П/6)/П - 0 = 1/3
 = \int\limits_{-\infty}^{+\infty} xf(x)dx = \int\limits_{-\infty}^{0} xf(x)dx + \int\limits_{0}^{1} xf(x)dx + \int\limits_{1}^{+\infty} xf(x)dx = )
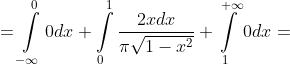
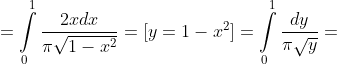
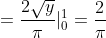
 = \int\limits_{-\infty}^{+\infty} x^{2}f(x)dx = \int\limits_{-\infty}^{0} x^{2}f(x)dx + \int\limits_{0}^{1} x^{2}f(x)dx + \int\limits_{1}^{+\infty} x^{2}f(x)dx = )
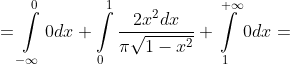
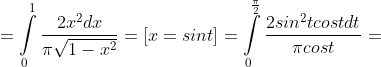
dt}{\pi} = )
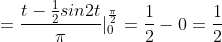
 = M(X^{2}) - M^{2}(X) = \frac{1}{2} - \frac{4}{\pi^{2} } = \frac{2\pi^{2} - 16}{4\pi^{2} } )
 = \sqrt{D(X)} = \frac{\sqrt{2\pi^{2} - 16} }{2\pi} )
(Сообщение отредактировал RKI 12 нояб. 2009 16:33)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 нояб. 2009 16:29 | IP
|
|
otan27
Новичок
|
RKI, благодарю за решения, всё-таки можно рассмотреть задачу - никак не вникну без цифр:
Имеется n урн, в каждой из которых по m белых и по k черных шаров. Из первой урны наудачу извлекается один шар и перекладывается во вторую. Затем из второй урны наудачу извлекается один шар и перекладывается в третью урну и т.д. Определить вероятность извлечения после такого перекладывания белого шара из белой урны.
|
Всего сообщений: 9 | Присоединился: ноябрь 2009 | Отправлено: 12 нояб. 2009 16:37 | IP
|
|
RKI
Долгожитель
|
Цитата: SvetYulya написал 12 нояб. 2009 14:47
3.Случайная величина X задана функцией распределения:
F(x) = {ln x, 1<x<e
{0, x<=1
{1, x>=e
Найти: плотность вероятности f(x),вероятность попадания случайной величины в интервал(1;2), среднеквадратическое отклонение X.
F(x) = {0, x <= 1
{lnx, 1 < x < e
{1, x >= e
f(x) = F'(x)
f(x) = {0, x < 1
{1/x, 1 < x < e
{0, x > e
P(1 < X < 2) = F(2) - F(1) = ln2 - 0 = ln2
 = \int\limits_{-\infty}^{+\infty} xf(x)dx = \int\limits_{-\infty}^{1} xf(x)dx + \int\limits_{1}^{e} xf(x)dx + \int\limits_{e}^{+\infty} xf(x)dx = )
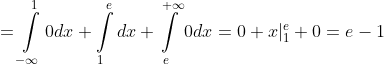
 = \int\limits_{-\infty}^{+\infty} x^{2}f(x)dx = \int\limits_{-\infty}^{1} x^{2}f(x)dx + \int\limits_{1}^{e} x^{2}f(x)dx + \int\limits_{e}^{+\infty} x^{2}f(x)dx = )
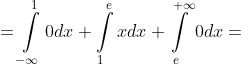
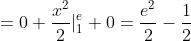
 = M(X^{2}) - M^{2}(X) = \frac{e^{2} }{2} - \frac{1}{2} - (e - 1)^{2} = )
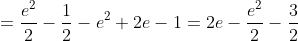
 = \sqrt{D(X)} = \sqrt{2e - \frac{e^{2} }{2} - \frac{3}{2} } )
(Сообщение отредактировал RKI 12 нояб. 2009 16:46)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 нояб. 2009 16:44 | IP
|
|
RKI
Долгожитель
|
Цитата: otan27 написал 12 нояб. 2009 16:37
вероятность извлечения после такого перекладывания белого шара из белой урны.
в задаче нигде ничего не указано про белую урну
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 нояб. 2009 16:48 | IP
|
|
|
Форум
Решение задач по теории вероятности
