RKI 
Долгожитель
|
   
Цитата: Cady написал 10 нояб. 2009 19:40
10.Монета бросается до тех пор, пока орел не выпадает 8 раз. Определить вероятность того, что при этом решка выпадает 4 раза.
A = {решка выпадет 4 раза при условии, что орел выпадет 8 раз}
A = A1*A2
A1 = {монета бросается 11 раз, при этом 7 раз выпадет орел и 4 раза - решка}
n = 11 - количество подбрасываний
p = 1/2 - вероятность выпадения решки
q = 1 - p = 1 - 1/2 = 1/2 - вероятность выпадения орла
m - количество выпадений решки
По формуле Бернулли
P(A1) = P(m=4) = C(4;11)*((1/2)^4)*((1/2)^7) =
= 330*((1/2)^11) = 330/2048 = 165/1024
A2 = {на двенадцатом подбрасывании выпадет орел (восьмой раз)}
P(A2) = 1/2
P(A) = P(A1*A2) = P(A1)P(A2) = (165/1024)*(1/2) = 165/2048
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 нояб. 2009 16:41 | IP
|
|
RKI
Долгожитель
|
Цитата: Cady написал 10 нояб. 2009 19:40
11.Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,002. Поступило 400 вызовов. Определить вероятность того, что будет более 3 «сбоев».
n = 400 - количество вызовов
p = 0.002 - вероятность сбоя при одном отдельном вызове
m - общее количество сбоев
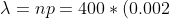 = 0.8 )
 = 1 - P(m \le 3) = )
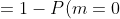 - P(m=1) - P(m=2) - P(m=3) = )
|
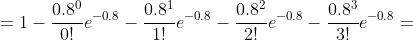
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 нояб. 2009 16:50 | IP
|
|
Fenja544
Новичок
|
всем помогаете, а про меня забыли!(((
Вероятность отказа выключателя равна 0,2. Найти сколько выключателей должно быть, чтобы вероятность одного отказа была 0,9
|
Всего сообщений: 40 | Присоединился: октябрь 2009 | Отправлено: 11 нояб. 2009 16:52 | IP
|
|
RKI
Долгожитель
|
Цитата: Cady написал 10 нояб. 2009 19:40
12.Вероятность наступления некоторого события в каждом из 100 независимых испытаний равна 0,4. Определить вероятность того, что число m наступлений события удовлетворяет неравенст-ву m меньше или равно 25.
n = 100 - количество независимых испытаний
p = 0.4 - вероятность наступления события в каждом отдельном испытании
q = 1 - p = 1 - 0.4 = 0.6
np = 100*(0.4) = 40
npq = 100*(0.4)*(0.6) = 24
По интегральной формуле Муавра-Лапласа
 = 0.5 + \Phi (\frac{25 - 40}{\sqrt{24} }) \sim 0.5 + \Phi (- 3.06) = )
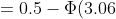 \sim 0.5 - 0.499 = 0.001 )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 нояб. 2009 16:54 | IP
|
|
RKI
Долгожитель
|
Цитата: Fenja544 написал 11 нояб. 2009 16:52
Вероятность отказа выключателя равна 0,2. Найти сколько выключателей должно быть, чтобы вероятность одного отказа была 0,9
В условиях задачи "ровно одного отказа" или "хотя бы одного отказа"
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 нояб. 2009 16:57 | IP
|
|
Fenja544
Новичок
|
точно не сказано, но видимо хотя бы одного
|
Всего сообщений: 40 | Присоединился: октябрь 2009 | Отправлено: 11 нояб. 2009 17:02 | IP
|
|
RKI
Долгожитель
|
Цитата: Cady написал 10 нояб. 2009 19:40
8.В первом ящике из 6 шаров 4 красных и 2 черных, во втором ящике из 7 шаров 2 красных и 5 черных. Из первого ящика во второй, переложили один шар, затем из второго в первый пере-ложили один шар. Найти вероятность того, что шар, извлеченный после этого из первого ящи-ка, черный.
H1 = {из первой урны во вторую переложили красный шар, а затем из второй урны в первую - также красный шар}
H2 = {из первой урны во вторую переложили черный шар, а затем из второй урны в первую - красный шар}
H3 = {из первой урны во вторую переложили красный шар, а затем из второй урны в первую - черный шар}
H4 = {из первой урны во вторую переложили черный шар, а затем из второй урны в первую - также черный шар}
P(H1) = (4/6)*(3/8) = 1/4
P(H2) = (2/6)*(2/8) = 1/12
P(H3) = (4/6)*(5/8) = 5/12
P(H4) = (2/6)*(6/8) = 1/4
A = {из первой урны достали черный шар}
A|H1 = {из первой урны достали черный шар при условии, что в ней 4 красных и 2 черных шара}
A|H2 = {из первой урны достали черный шар при условии, что в ней 5 красных и 1 черный шар}
A|H3 = {из первой урны достали черный шар при условии, что в ней 3 красных и 3 черных шара}
A|H4 = {из первой урны достали черный шар при условии, что в ней 4 красных и 2 черных шара}
P(A|H1) = 2/6 = 1/3
P(A|H2) = 1/6
P(A|H3) = 3/6 = 1/2
P(A|H4) = 2/6 = 1/3
По формуле полной вероятности
P(A) =
= P(H1)P(A|H1) + P(H2)P(A|H2) + P(H3)P(A|H3) + P(H4)P(A|H4) =
= (1/4)*(1/3) + (1/12)*(1/6) + (5/12)*(1/2) + (1/4)*(1/3) =
= 1/12 + 1/72 + 5/24 + 1/12 = (6 + 1 + 15 + 6)/72 =
= 28/72 = 7/18
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 нояб. 2009 17:21 | IP
|
|
RKI
Долгожитель
|
Цитата: Fenja544 написал 11 нояб. 2009 16:52
Вероятность отказа выключателя равна 0,2. Найти сколько выключателей должно быть, чтобы вероятность одного отказа была 0,9
Решение при условии: "хотя бы одного отказа"
n - количество выключателей
p = 0.2 - вероятность отказа выключателя
q = 1 - p = 1 - 0.2 = 0.8
m - количество отказов
По условию задачи P(m >= 1) = 0.9
С другой стороны
P(m >= 1) = 1 - P(m < 1) = 1 - P(m=0) = 1 - (0.8)^n = 0.9
(0.8)^n = 0.1
 - посчитайте на калькуляторе
(Сообщение отредактировал RKI 11 нояб. 2009 17:27)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 нояб. 2009 17:26 | IP
|
|
fhbfyf
Новичок
|
Помогите решит задачку)))
Одновременно бросаются 2 игральные кости. Найти вероятность того,что на каждой кости появится нечетное количество очков.
|
Всего сообщений: 2 | Присоединился: ноябрь 2009 | Отправлено: 11 нояб. 2009 17:44 | IP
|
|
malna
Новичок
|
Добрый вечер! Ещё задачку решила, проверьте пожалуйста, верно ли.
Интервалы времени между приходами в порт судов распределены по показательному закону с интенсивностью =5(часов). Найти числовые характеристики Х- время между приходами двух судов. Вычислить:а) Р(Х (1,2)); б)Р(Х (4,6)).
Решение:
=5, т.к. это показательное распределение, то Р(а<x<b)=e^-a – e^-b, следовательно
а) Р(Х (1,2))=е^-5 – e^-10= 0,0067
б) Р(Х (4,6))=e^-20 – e^-30= 2,1*10^-9
MX=1/=0,2 математическое ожидание
DX=1/^2=0,04 дисперсия
б(х)=0,2 среднее квадратичное отклонение
V(х) =? Коэффициент вариации
Медиана (х)=ln^2/= 0,694/5=0,1388
Огрооооооооомное спасибо за помощь.
|
Всего сообщений: 8 | Присоединился: ноябрь 2009 | Отправлено: 11 нояб. 2009 18:17 | IP
|
|
|
Форум
Решение задач по теории вероятности
