RKI 
Долгожитель
|
   
Цитата: Dasha 2009 написал 10 нояб. 2009 19:31
Делается 8 выстрелов по цели.Вероятность попадания в цель при каждом выстреле = 0,6. Пусть Х - число попаданий в цель. Найти функцию распределения случайной величины Х. Определить вероятность того, что будет не меньше 7 попаданий в цель. Найти М(х) и D(х)
n = 8 - количество выстрелов
p = 0.6 - вероятность попадания при одном выстреле
q = 1 - p = 1 - 0.6 = 0.4
Случайная величина X - число попаданий в цель.
Событие {X=k} означает, что k раз произошло попадание в цель и (8-k) раз были промахи, k = 0,1,2,...8.
Данная случайная величина распределена по закону Бернулли.
P(X=k) = C(k;8)*((0.6)^k)*((0.4)^(8-k)), k = 0,1,2,...,8.
P(X=0) = (0.4)^8 = 0.00065536
P(X=1) = 8*(0.6)*((0.4)^7) = 0.00786432
P(X=2) = 28*((0.6)^2)*((0.4)^6) = 0.04128768
P(X=3) = 56*((0.6)^3)*((0.4)^5) = 0.12386304
P(X=4) = 70*((0.6)^4)*((0.4)^4) = 0.2322432
P(X=5) = 56*((0.6)^5)*((0.4)^3) = 0.27869184
P(X=6) = 28*((0.6)^6)*((0.4)^2) = 0.20901888
P(X=7) = 8*((0.6)^7)*(0.4) = 0.08957952
P(X=8) = (0.6)^8 = 0.01679616
Закон распределения случайной величины X имеет вид:
X 0 1 2 3
P 0.00065536 0.00786432 0.04128768 0.12386304
X 4 5 6 7
P 0.2322432 0.27869184 0.20901888 0.08957952
X 8
P 0.01679616
Функция распределения случайной величины X имеет вид:
F(x) = {0, x <= 0
{0.00065536, 0 < x <= 1
{0.00851968, 1 < x <= 2
{0.04980736, 2 < x <= 3
{0.1736704, 3 < x <= 4
{0.4059136, 4 < x <= 5
{0.68460544, 5 < x <= 6
{0.89362432, 6 < x <= 7
{0.98320384, 7 < x <= 8
{1, x > 8
P(X >= 7) = P(X=7) + P(X=8) = 0.08957952 + 0.01679616 =
= 0.106367568
M(X) = np = 8*(0.6) = 4.8
D(X) = npq = 8*(0.6)*(0.4) = 1.92
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 23:22 | IP
|
|
Ytochka88
Новичок
|
Плиссссссссс.а вот еще задачки!!!!!!!
1.Два судна могут подойти к причалу в любое время в течение суток независимо. На причале одно место для разгрузки. Разгрузка длится 4 часа. Какова вероятность того, что одно из судов будет ждать более часа?
2.Игральная кость бросается 24 раза. Определить вероятность того, что: а) шесть очков появилось хотя бы один раз; б) шесть очков не появилось ни разу; в) шесть очков появилось больше двух раз.
3.На каждый лотерейный билет с вероятностью 0,1 может выпасть крупный выигрыш, с вероятностью 0,35 - мелкий выигрыш и с вероятностью 0,55 билет может оказаться без выигрыша. Куплено 10 билетов. Определить вероятность получения ровно 0 крупных выигрышей и 4 мелких.
4.Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,007. Поступило 1000 вызовов. Определить вероятность того, что будет не менее 2 «сбоев».
5.Вероятность наступления некоторого события в каждом из 400 независимых испытаний равна 0,7. Определить вероятность того, что число m наступлений события удовлетворяет неравенству m≥295.
 
|
Всего сообщений: 6 | Присоединился: ноябрь 2009 | Отправлено: 10 нояб. 2009 23:28 | IP
|
|
RKI
Долгожитель
|
Цитата: Ivan26 написал 10 нояб. 2009 22:39
В ящике находятся 30 деталей ,выполненных первым рабочим,40 деталей,изготовленных вторым рабочим и 50 деталей,сделанных третьим рабочим.Известно,что брак,который рабочие могут допустить при работе, составляет 10%,20% и 30% соответственно для каждого рабочего. Найти вероятность того,что одна деталь,вынутая из ящика,окажется бракованной.
H1 = {деталь выполнена первым рабочим}
H2 = {деталь выполнена вторым рабочим}
H3 = {деталь выполнена третьим рабочим}
P(H1) = 30/(30+40+50) = 30/120 = 3/12
P(H2) = 40/120 = 4/12
P(H3) = 50/120 = 5/12
A = {деталь бракованная}
A|H1 = {деталь бракованная при условии, что она выполнена первым рабочим}
A|H2 = {деталь бракованная при условии, что она выполнена вторым рабочим}
A|H3 = {деталь бракованная при условии, что она выполнена третьим рабочим}
P(A|H1) = 0.1
P(A|H2) = 0.2
P(A|H3) = 0.3
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) + P(H3)P(A|H3) =
= (3/12)*(0.1) + (4/12)*(0.2) + (5/12)*(0.3) =
= (0.3)/12 + (0.8)/12 + (1.5)/12 = (2.6)/12 = (1.3)/6 =
= 13/60
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 23:29 | IP
|
|
Ivan26
Новичок
|
Cпасибо!!
|
Всего сообщений: 5 | Присоединился: ноябрь 2009 | Отправлено: 10 нояб. 2009 23:31 | IP
|
|
RKI
Долгожитель
|
Цитата: Ytochka88 написал 10 нояб. 2009 23:28
3.На каждый лотерейный билет с вероятностью 0,1 может выпасть крупный выигрыш, с вероятностью 0,35 - мелкий выигрыш и с вероятностью 0,55 билет может оказаться без выигрыша. Куплено 10 билетов. Определить вероятность получения ровно 0 крупных выигрышей и 4 мелких.
n = 10 - количество билетов
p1 = 0.1 - вероятность крупного выигрыша
p2 = 0.35 - вероятность мелкого выигрыша
p3 = 0.55 - вероятность проигрыша
p1 + p2 + p3 = 0.1 + 0.35 + 0.55 = 1
m1 - количество билетов с крупным выигрышем
m2 - количество билетов с мелким выигрышем
m3 - количество проигрышных билетов
m1 + m2 + m3 = n = 10
По полиномиальной схеме Бернулли
P(m1 = 0, m2 = 4, m3 = 6) =
= 10!/0!4!6! * ((0.1)^0) * ((0.35)^4) * ((0.55)^6) =
= 0.0872303488095703125
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 23:37 | IP
|
|
SvetYulya
Новичок
|
RKI, Вы про нас не забыли?
|
Всего сообщений: 11 | Присоединился: ноябрь 2009 | Отправлено: 10 нояб. 2009 23:40 | IP
|
|
RKI
Долгожитель
|
Цитата: Ytochka88 написал 10 нояб. 2009 23:28
4.Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,007. Поступило 1000 вызовов. Определить вероятность того, что будет не менее 2 «сбоев».
n = 1000 - количество вызовов
p = 0.007 - вероятность сбоя при одном отдельном вызове
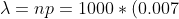 = 7 )
m - количество сбоев
 = 1 - P(m < 2) = 1 - P(m=0) - P(m=1) = )
|
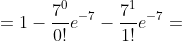
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 23:42 | IP
|
|
RKI
Долгожитель
|
Цитата: SvetYulya написал 10 нояб. 2009 23:40
RKI, Вы про нас не забыли?
Нет, я про Вас не забыла.
Если Вам будет не поздно, я Вам завтра с утра напишу Ваше решение
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 23:44 | IP
|
|
SvetYulya
Новичок
|
Хорошо,будем очень признательны.
|
Всего сообщений: 11 | Присоединился: ноябрь 2009 | Отправлено: 10 нояб. 2009 23:46 | IP
|
|
RKI
Долгожитель
|
Цитата: SvetYulya написал 10 нояб. 2009 23:46
Хорошо,будем очень признательны.
Я завтра утром первым Вам отвечу.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 23:49 | IP
|
|
|
Форум
Решение задач по теории вероятности
