RKI 


Долгожитель
|
    
Цитата: Dasha 2009 написал 10 нояб. 2009 11:45
Из партии в 1500 штук деталей, из которых 90 "плюсовых", производится выборка (с возвратом) в n = 50 штук. Какова вероятность того, что "плюсовых" деталей окажется m = 0, 1, 2, ...; не более трех; более двух; не менее одной и не более пяти?
n = 50
p = 90/1500 = 0.06
 = 3 )
По формуле Пуассона
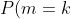 = \frac{\lambda^{k} }{k!}e^{-\lambda} = \frac{3^{k} }{k!}e^{-3} )
 = P(m=0) + P(m=1) + P(m=2) + P(m=3) = )
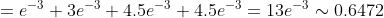
 = 1 - P(m \le 2) = 1 - P(m=0) - P(m=1) - P(m=2) = )
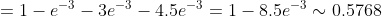
 = )
 + P(m=2) + P(m=3) + P(m=4) + P(m=5) = )
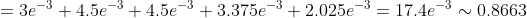
(Сообщение отредактировал RKI 10 нояб. 2009 12:42)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 12:40 | IP
|
|
Ivan26

Новичок
|
     
Помогите,пожалуйста!!!
Плотность вероятности случайной величины
f(x)= 1/корень 4.5П e в степени -х2-4х-4 делённое на 4.5
Найти её математическое ожидание, дисперсию, построить кривую вероятности; найти вероятности событий:А-случайная величина примет только положительные значения, В-случайная величина попадает в интервал, симметричный относительно математического ожидания, длиной два средних квадратных отклонения.
(Сообщение отредактировал Ivan26 10 нояб. 2009 13:29)
|
Всего сообщений: 5 | Присоединился: ноябрь 2009 | Отправлено: 10 нояб. 2009 13:26 | IP
|
|
Dasha 2009

Новичок
|
    
Большое спасибо))))))
|
Всего сообщений: 13 | Присоединился: ноябрь 2009 | Отправлено: 10 нояб. 2009 13:49 | IP
|
|
SvetYulya


Новичок
|
     
Цитата: SvetYulya написал 9 нояб. 2009 19:04
Спасибо за задачу, насчет первой уточним у преподавателя. Не могли бы Вы решить еще 2 задачи:
1. На 10 одинаковых карточках написано различные числа от 0 до 9. Определить вероятность того, что на удачу образованное с помощью данных карточек трехзначное число делиться на 36.
Вот наше предполагаемое решение, проверьте пожалуйста:
A = {трехзначное число делится на 36}
С(3;10)=(10*9*8)/(1*2*3)=120
С(3;24)=(24*23*22)/(1*2*3)=2024
Р(А)=С(3;10)/С(3;24)=120/2024=0,0592
|
Всего сообщений: 11 | Присоединился: ноябрь 2009 | Отправлено: 10 нояб. 2009 14:02 | IP
|
|
tatank4

Новичок
|
    
Пмогите пожалуста!!!! завтра контрольная!!!!
1.В соревнованиях по футболу участвуют 20 команд. Случайным образом они делятся на две группы по 10 команд. Какова вероятность того, что 2 наиболее сильные команды при этом окажутся в одной группе?
2.Несколько раз бросают игральную кость. Какова вероятность того, что шесть очков появится впервые при шестом бросании?
3.Четыре шарика случайным образом разбрасываются по семи лункам. Каждый шарик с равной вероятностью и независимо от других попадает в любую лунку. Определить вероятность того, что: а) все шарики попадут в разные лунки; б) хотя бы два шарика попадут в одну лунку.
4.На отрезке [0, 1] случайным образом выбираются три числа x, y и z. Найти вероятность того, что их сумма больше 1.
5.Два судна могут подойти к причалу в любое время в течение суток независимо. На причале одно место для разгрузки. Разгрузка длится 4 часа. Какова вероятность того, что одно из судов будет ждать более часа?
6.В двух партиях процент доброкачественных изделий 82 и 36 соответственно. Наудачу выби-рают по одному изделию из каждой партии. Какова вероятность обнаружить среди них: а) хотя бы одно бракованное; б) два бракованных; в) одно доброкачественное и одно брако-ванное?
7.Из 1000 ламп 810 принадлежат 1-й партии, 70 - второй, остальные третьей. В первой партии 10%, во второй 1%, в третьей 2% бракованных ламп. Наудачу выбирается одна лампа. Опреде-лить вероятность того, что выбранная лампа бракованная.
8.В альбоме 4 чистых и 8 гашеных марок. Из них наудачу извлекаются 6 марок, подвергаются спецгашению и возвращаются в альбом. После этого вновь наудачу извлекается 4 марки. Оп-ределить вероятность того, что все они чистые.
9.Игральная кость бросается 24 раза. Определить вероятность того, что: а) шесть очков появи-лось хотя бы один раз; б) шесть очков не появилось ни разу; в) шесть очков появилось больше двух раз.
10.На каждый лотерейный билет с вероятностью 0,1 может выпасть крупный выигрыш, с вероят-ностью 0,35 - мелкий выигрыш и с вероятностью 0,55 билет может оказаться без выигрыша. Куплено 10 билетов. Определить вероятность получения ровно 0 крупных выигрышей и 4 мелких.
11.Вероятность «сбоя» в работе телефонной станции при каждом вызове равна 0,007. Поступило 1000 вызовов. Определить вероятность того, что будет не менее 2 «сбоев».
12.Вероятность наступления некоторого события в каждом из 400 независимых испытаний равна 0,7. Определить вероятность того, что число m наступлений события удовлетворяет неравенству m≥295.
заранее спасибо!!)))
|
Всего сообщений: 7 | Присоединился: ноябрь 2009 | Отправлено: 10 нояб. 2009 14:27 | IP
|
|
0ksf0rd


Новичок
|
    
Помогите бедным студентам, пожалуйста!
Плоскость разграфлена параллельными линиями с шагом 2см. На плоскость бросается монета диаметром 1,5 см. Определить вероятность того, что она не пересечет ни одну из линий.
Совсем не представляю, как решать 
|
Всего сообщений: 2 | Присоединился: ноябрь 2009 | Отправлено: 10 нояб. 2009 15:15 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Ivan26 написал 10 нояб. 2009 13:26
Плотность вероятности случайной величины
f(x)= 1/корень 4.5П e в степени -х2-4х-4 делённое на 4.5
Найти её математическое ожидание, дисперсию, построить кривую вероятности; найти вероятности событий:А-случайная величина примет только положительные значения, В-случайная величина попадает в интервал, симметричный относительно математического ожидания, длиной два средних квадратных отклонения.
 = \frac{1}{\sqrt{4.5\pi} }e^{\frac{-x^{2}-4x-4}{4.5} } = \frac{1}{\sqrt{4.5} }e^{-\frac{-(x+2)^{2} }{4.5} } )
По виду плотности распределения можно утверждать, что случайная величина X имеет нормальное распределение с параметрами:
 - математическое ожидание - математическое ожидание
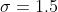 - среднее квадратическое отклонение - среднее квадратическое отклонение
 = \sigma^{2} = 2.25 ) - дисперсия - дисперсия
 = P(X > 0) = 0.5 - \Phi (\frac{0 + 2}{1.5}) \sim )
 \sim 0.5 - 0.4082 = 0.0918 )
 = P(|X-a| < \sigma) = P(-\sigma < X - a < \sigma) = )
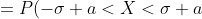 = \Phi (\frac{\sigma + a - a}{\sigma}) - \Phi (\frac{-\sigma + a - a}{\sigma}) = )
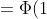 - \Phi (-1) = \Phi (1) + \Phi (1) = 2\Phi (1) = 2*(0.3413) = 0.6826 )
(Сообщение отредактировал RKI 10 нояб. 2009 16:35)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 16:32 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: SvetYulya написал 9 нояб. 2009 19:04
1. На 10 одинаковых карточках написано различные числа от 0 до 9. Определить вероятность того, что на удачу образованное с помощью данных карточек трехзначное число делиться на 36.
Карточки достаются с возвращением или нет?
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 16:44 | IP
|
|
SvetYulya


Новичок
|
     
задача так дана, никаких условий больше нет,если можно напишите пожалуйста два варианта решения
|
Всего сообщений: 11 | Присоединился: ноябрь 2009 | Отправлено: 10 нояб. 2009 16:52 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: tatank4 написал 10 нояб. 2009 14:27
1.В соревнованиях по футболу участвуют 20 команд. Случайным образом они делятся на две группы по 10 команд. Какова вероятность того, что 2 наиболее сильные команды при этом окажутся в одной группе?
A = {2 наиболее сильные команды окажутся в одной группе}
Посчитаем число n всевозможных исходов. Способов разбить 20команд на 2 группы (по 10 команд):
n = 20!/10!10!.
Посчитаем число m исходов, благоприятных событию A. Первая сильная команда может выбрать одну из двух групп, то есть первая команда имеет m1 = 2 альтернативы. Вторая сильная команда имеет только m2 = 1 альтернативу: вступить в ту же самую группу, что и первая сильная команда. Способов разбить остальные 18 команд на две группы (8 команд в одной, и 10 - в другой):
m3 = 18!/8!10!.
По правилу произведения
m = m1*m2*m3 = 2*1*18!/8!10! = 2*18!/8!10!.
По классическому определению вероятности
P(A) = m/n = (2*18!*10!*10!)/(8!*10!*20!) =
= (2*18!*10!)/(8!*20!) = (2*9*10)/(19*20) = 9/19
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 16:54 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности