Dasha 2009
Новичок
|
   
Новичок
Помогите пожайлуста:
Из партии в 1500 штук деталей, из которых 90 "плюсовых", производится выборка (с возвратом) в n = 50 штук. Какова вероятность того, что "плюсовых" деталей окажется m = 0, 1, 2, ...; не более трех; более двух; не менее одной и не более пяти?
|
Всего сообщений: 13 | Присоединился: ноябрь 2009 | Отправлено: 9 нояб. 2009 22:32 | IP
|
|
RKI 
Долгожитель
|
Цитата: SvetYulya написал 9 нояб. 2009 19:04
2.В двух урнах находяться шары, отличающиеся только по цвету, причем в 1ой урне 6 белых, 10 черных и 6 красных шаров, а во второй соответственно 8,8,4. Из обеих урн на удачу извлекаются по одному шару. Какова вероятность,что оба шара разного цвета.
A = {оба шара разного цвета}
не A = {оба шара одинакового цвета}
не A = A1 + A2 + A3
A1 = {оба шара белого цвета}
A1 = B1*B2
B1 = {из первой урны достали белый шар}
P(B1) = 6/(6+10+6) = 6/22 = 3/11
B2 = {из второй урны достали белый шар}
P(B2) = 8/(8+8+4) = 8/20 = 2/5
P(A1) = P(B1*B2) = P(B1)*P(B2) = (3/11)*(2/5) = 6/55
A2 = {оба шара черного цвета}
A2 = C1*C2
C1 = {из первой урны достали черный шар}
P(C1) = 10/22 = 5/11
C2 = {из второй урны достали черный шар}
P(C2) = 8/20 = 2/5
P(A2) = P(C1*C2) = P(C1)*P(C2) = (5/11)*(2/5) = 10/55
A3 = {оба шара красного цвета}
A3 = D1*D2
D1 = {из первой урны достали красный шар}
P(D1) = 6/22 = 3/11
D2 = {из второй урны достали красный шар}
P(D2) = 4/20 = 1/5
P(A3) = P(D1*D2) = P(D1)*P(D2) = (3/11)*(1/5) = 3/55
P(не A) = P(A1 + A2 + A3) = P(A1) + P(A2) + P(A3) =
= 6/55 + 10/55 + 3/55 = 19/55
P(A) = 1 - P(не A) = 1 - 19/55 = 36/55
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 9:12 | IP
|
|
RKI
Долгожитель
|
Цитата: SvetYulya написал 9 нояб. 2009 19:04
И проверьте пожалуйста вот эти:
1. Вычислить вероятность того, что при бросании двух игральных костей сумма очков на верхних гранях будет больше 10, если разность больше 2.
РЕШЕНИЕ:
A = {сумма очков больше 10}
B = {разность очков больше 2} = {(6;1); (1;6);(6;2);(2;6);(6;3);(3;6);(5;1);(1;5);(5;2);(2;5);(4;1);(1;4)}
|B| = 12
AB = {сумма очков больше 10 и разность очков больше 2}
|AB| = 0
P(A|B) = |AB|/|B| = 0/12 = 0
Верно
2. Вероятность выигрыша по одному билету лотереи равна 1/4. Какова вероятность того. Что лицо, имеющее шесть билетов не выиграет по двум билетам.
РЕШЕНИЕ:
A = {не выиграет по двум билетам}
р=1/4
k=2
n=6
q=1-р=1-1/4=3/4
Р(А)=С(2;6)*(1/4)^2*(3/4)^4=15*1/16*81/256=0,29663
Не верно!
n = 6 - количество билетов
p = 1/4 - вероятность выигрыша по одному билету
q = 1 - 1/4 = 3/4
m - количество билетов, по которым будет выигрыш
A = {не выиграет по двум билетам} = {выиграет по 4 билетам и проиграет по 2 билетам}
P(A) = P(m=4) = C(4;6)*((1/4)^4)*((3/4)^2) =
= 15*(1/256)*(9/16) = 135/4096 = 0.032958984375
3. На трех станках обрабатываются однотипные детали; вероятность брака для станка № 1 составляет 0,06, а для станков № 2 №3 - 0,05. Обработанные детали складываются в одном месте, причем станок № 1 обрабатывает вдвое больше деталей, чем станок № 2 и втрое больше, чем станок №3 . Вычислить вероятность того, что взятая наудачу деталь не будет бракованной.
РЕШЕНИЕ:
H1 = {деталь обработана на первом станке}
H2 = {деталь обработана на втором станке}
H3 = {деталь обработана на третьем станке}
P(H1) = 6/11
P(H2) = 3/11
P(H3) = 2/11
A = {деталь не будет бракованной}
P(A|H1) = 1 - 0.06 = 0.94
P(A|H2) = 1 - 0.05 = 0.95
P(A|H3) = 1 - 0.05 = 0.95
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2)+ P(H3)P(A|H3) =
= (6/11)*(0.94) + (3/11)*(0.95)+ (2/11)*(0.95) = 2.92/3 =
= 10,39/11 = 0,94
Принцип решения верен.
Одно замечание. Если Вы округляете ответ, то в теории вероятностей как правило берут 4 цифры после запятой (иногда и больше)
P(A) = (10.39)/11 ~ 0.9445
4. Корректура в 1000 страниц содержит 500 опечаток, найти вероятность того, что на странице не меньше трех опечаток.
РЕШЕНИЕ:
лямбда = 500/1000 = 0.5
По теореме Пуассона
P(m=0) = ( (0.5^0)/0! )*e^(-1/2) = e^(-1/2) = 0.6065
P(m=1) = ( (0.5^1)/1! )*e^(-1/2) = 0.5*e^(-2) = 0.3033
P(m=2) = ( (0.5^2)/2! )*e^(-1/2) = 0,0758
P(m=3) = ( (0.5^3)/3! )*e^(-1/2) = 0,0126
A = {на странице окажется не меньше трех опечаток}
P(A) = P(m>=3) = 1 - P(m<3) = 1 - P(m=0) - P(m=1)- P(m=2)- P(m=3) = 1-0.6065 - 0.3033- 0,0758-0,0126=0,0018
Верно
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 9:30 | IP
|
|
RKI
Долгожитель
|
Цитата: SvetYulya написал 9 нояб. 2009 19:04
5. Вероятность неточной сборки прибора равна 0,15. Найти вероятность того, что среди 500
приборов окажется от 400 до 480 (включительно) точных.
РЕШЕНИЕ:
n = 500
p =0,15
q = 1-p =0,85
np = 75
npq = 64
sqrt(npq) = 8
А = {от 400 до 480 точных приборов}
m1 = 400
x1 = (m1 - np)/sqrt(npq) = (400 - 75)/8 = 40,625
m2 = 480
x2 = (m2 - np)/sqrt(npq) = (480 - 75)/8 =50,625
По интегральной теореме Муавра-Лапласа
P(А) = P(m1<=m<=m2) = Ф(x2) - Ф(x1) = Ф(50,625) - Ф(40,625) = 0,5-0,5=0
Неверно!
n = 500 - общее количество приборов
q = 0.15 - вероятность того, что отдельно взятый прибор неточен
p = 1 - 0.15 = 0.85 - вероятность того, что отдельно взятый прибор точен
np = 500*(0.85) = 425
npq = 500*(0.85)*(0.15) = 63.75
A = {от 400 до 480 точных приборов}
m1 = 400
x1 = (400 - 425)/sqrt(63.75) ~ - 3.13
m2 = 480
x2 = (480 - 425)/sqrt(63.75) ~ 6.89
P(A) = P(m1 <= m <= m2) = Ф(x2) - Ф(x1) ~ Ф(6.89) - Ф(-3.13) =
= Ф(6.89) + Ф(3.13) ~ 0.5 + 0.499 = 0.999
6.При стрельбе была получена частотность попадания 0,6. Сколько было сделано выстрелов, если получено 12 промахов.
Решение:
W(A)= m/n
W(A)=0,6. m=12. Найдем n.
n= m/W(A) = 12 / 0,6 = 20.
Неверно
W(A) - частотность промахов
W(A) = 1 - 0.6 = 0.4
m - количество промахов
n - количество выстрелов
m = 12
W(A) = m/n = 12/n = 0.4
n = 30
7.Вероятность выживания бактерий после радиоактивного облучения равна 0,004. Найти вероятность того, что после облучения из 500 бактерий останется более трех бактерий.
Решение:
Число n=500 велико, вероятность р=0,004 мала и рассматриваемые события(выживания бактерий) независимы, поэтому имеет место формула Пуассона.
Найдем лямбда:
лямбда = 500/1000 = 0.5
P(m=0) = ( (2^0)/0! )*e^(-2) =e^(-2)~ 0.1353
P(m=1) = (2^1)(e^(-2))/1!=2(e^(-2)) ~ 0.27067
P(m=2) = (2^2)(e^(-2))/2!=4*e^(-2)/2=2(e^(-2)) ~0.27067
P(m=3) = (2^3)(e^(-2))/3!=8*e^(-2)/6=4*e^(-2)/3 ~ 0.1804
A = {выживет более трех бактерий}
P(A) = P(m>3) = 1 - (P(m=0) + P(m=1)+P(m=2) + P(m=3)) =1-(0.1353+0.27067+0.27067+0.1804)=1-0,85704=0,14296
лямбда = 500*(0,004) = 2
У Вас написано лямбда другое, но используете в задаче 2.
Остальное верно
Одно замечание: либо берете пять цифр после запятой, либо четыре. А не в разброс - то четыре, то пять
8. Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2.Найти вероятность того, что из 750 покупателей не более 120 потребуется обувь именно этого размера.
Решение:
По условию
n=750
p=0,2
k1=0
k2=120
Вычислим x' и x'' .
q=0.8
x'= k1-np/ sqrt (npq) = 0-750*0,2/ sqrt(750*0.2*0.8) = -150/spq(120)= -13.7
x''= k2-np/ sqrt (npq)= 120-750*0.2/ sqrt(750*0.2*0.8)= -2.73
Ф(х2)= Ф(-2,73)=-Ф(2,73)=-0,497
Ф(х1)= Ф(-13,7)=-Ф(13,7)=-0,5
Р750(0;120)=-0,497+0,5=0,003
Внимательно считайте
x' ~ - 13.69
x'' ~ - 2.74
P(0 <= m <= 120) = Ф(-2.74) - Ф(-13.69) = -Ф(2.74) + Ф(13.69) ~
~ - 0.4969 + 0.5 = 0.0031
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 9:47 | IP
|
|
RKI
Долгожитель
|
Цитата: Lenusik написал 9 нояб. 2009 18:43
3.На каждый лотерейный билет с вероятностью 0,12 может выпасть крупный выигрыш, с веро-ятностью 0,38 - мелкий выигрыш и с вероятностью 0,5 билет может оказаться без выигрыша. Куплено 13 билетов. Определить вероятность получения ровно 2 крупных выигрышей и 0 мелких.
n = 13 - количество купленных билетов
p1 = 0.12 - вероятность получить крупный выигрыш
p2 = 0.38 - вероятность получить мелкий выигрыш
p3 = 0.5 - вероятность проигрыша
p1 + p2 + p3 = 0.12 + 0.38 + 0.5 = 1
m1 - количество билетов с крупным выигрышем
m2 - количество билетов с мелким выигрышем
m3 - количество проигрышных билетов
m1 + m2 + m3 = n = 13
A = {2 крупных выигрыша, 0 мелких выигрышей}
По полиномиальной формуле Бернулли
P(A) = P(m1 = 2, m2 = 0, m3 = 11) =
= 13!/2!0!11! * ((0.12)^2)*((0.38)^0)*((0.5)^11) =
= 78*(0.0144)*(0.00048828125) = 0.0005484375
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 10:22 | IP
|
|
RKI
Долгожитель
|
Цитата: Lenusik написал 9 нояб. 2009 18:43
2.Готовясь к вступительному экзамену по математике, абитуриент должен подготовить 20 во-просов по математическому анализу и 25 по геометрии. Однако он успел подготовить только 15 вопросов по математического анализу и 20 по геометрии. Билет содержит 3 вопроса, 2 из них - по элементам математического анализа и 1 - по геометрии. Какова вероятность, что: а) студент сдаст экзамен на отлично (ответит на все три вопроса); б) на хорошо (ответит на один вопрос из математического анализа и один из геометрии)?
Посчитаем число n всевозможных исходов. Способов выбрать 2 билета по математическому анализу из 20 имеющихмя
n1 = C(2;20) = 20!/2!18! = 190.
Способов выбрать 1 билет по геометрии из 25 имеющихся
n2 = C(1;25) = 25!/1!24! = 25.
По правилу произведения
n = n1*n2 = 190*25 = 4750.
а) A = {студент ответит на все три вопроса}
Посчитаем число m исходов, благоприятных событию A. Способов выбрать 2 билета по математическому анализу из 15 выученных студентом:
m1 = C(2;15) = 15!/2!13! = 105.
Способов выбрать 1 билет по геометрии из 20 выученных студентом:
m2 = C(1;20) = 20!/1!19! = 20.
По правилу произведения
m = m1*m2 = 105*20 = 2100.
По классическому определению вероятности
P(A) = m/n = 2100/4750 = 42/95.
б) B = {студент ответит на 1 вопрос по математическому анализу и на 1 вопрос по геометрии}
Посчитаем число k исходов, благоприятных событию B. Способов выбрать 1 вопрос по математическому анализу из 15 выученных студентом:
k1 = C(1;15) = 15!/1!14! = 15.
Способов выбрать 1 вопрос по математическому анализу из 5 неизвестных студенту:
k2 = C(1;5) = 5!/1!4! = 5.
Способов выбрать 1 вопрос по геометрии из 20 выученных студентом:
k3 = C(1;20) = 20!/1!19! = 20.
По правилу произведения
k = k1*k2*k3 = 15*5*20 = 1500.
По классическому определению вероятности
P(B) = k/n = 1500/4750 = 6/19.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 10:49 | IP
|
|
RKI
Долгожитель
|
Цитата: Lenusik написал 9 нояб. 2009 18:43
1.Из колоды содержащей 54 карты (2 Джокера) вынимается наугад 5. Найти вероятность комби-нации “каре” – четыре карты одного номинала (Джокер заменяет любую карту).
A = {комбинация "каре"}
A = A1 + A2 + A3 + A4 + B1 + B2 + B3 + B4 + C1 + C2 + C3 + C4
Посчитаем число n всевозможных исходов для каждого из событий Ai, Bi, Ci (i=1,2,3,4).
Способов выбрать 4 карты из 54 имеющихся:
n = C(4;54) = 54!/4!50! = 316251.
A1 = {четыре карты масти "пики"}
A2 = {четыре карты масти "крести"}
A3 = {четыре карты масти "червы"}
A4 = {четыре карты масти "буби"}
Посчитаем число l исходов, благоприятных каждому событию Ai (i=1,2,3,4).
Всего карт в колоде (без двух Джокеров) 54 - 2 = 52. Карт одной отдельной масти в колоде 52:4 = 13.
Способов выбрать 4 карты одной отдельной масти (из 13 имеющихся):
l = C(4;13) = 13!/4!9! = 715.
По классическому определению вероятности
P(A1) = P(A2) = P(A3) = P(A4) = l/n = 715/316251.
B1 = {один Джокер и три карты масти "пики"}
B2 = {один Джокер и три карты масти "крести"}
B3 = {один Джокер и три карты масти "червы"}
B4 = {один Джокер и три карты масти "буби"}
Посчитаем число k исходов, благоприятных каждому из событий Bi (i=1,2,3,4).
Способов выбрать 1 Джокер из 2 имеющихся:
k1 = C(1;2) = 2!/1!1! = 2.
Способов выбрать 3 карты одной отдельно взятой масти из 13 имеющихмя:
k2 = C(3;13) = 13!/3!10! = 286.
По правилу произведения
k = k1*k2 = 2*286 = 572.
По классическому определению вероятности
P(B1) = P(B2) = P(B3) = P(B4) = k/n = 572/316251.
C1 = {два Джокера и две карты масти "пики"}
C2 = {два Джокера и две карты масти "крести"}
C3 = {два Джокера и две карты масти "червы"}
C4 = {два Джокера и две карты масти "буби"}
Посчитаем число m исходов, благоприятных каждому из событий Ci (i=1,2,3,4).
Способов выбрать 2 Джокера из 2 имеющихcя:
m1 = C(2;2) = 2!/0!2! = 1.
Способов выбрать 2 карты одной отдельно взятой масти из 13 имеющихся:
m2 = C(2;13) = 13!/2!11! = 78.
По правилу произведения
m = m1*m2 = 1*78 = 78.
По классическому определению вероятности
P(C1) = P(C2) = P(C3) = P(C4) = m/n = 78/316251.
P(A) =
= P(A1 + A2 + A3 + A4 + B1 + B2 + B3 + B4 + C1 + C2 + C3 + C4) =
= P(A1) + P(A2) + P(A3) + P(A4) + P(B1) + P(B2) + P(B3) + P(B4) + P(C1) + P(C2) + P(C3) + P(C4) =
= 4P(A1) + 4P(B1) + 4P(C1) =
= 2860/316251 + 2288/316251 + 312/316251 =
= 5460/316251 = 140/8109
(Сообщение отредактировал RKI 10 нояб. 2009 11:35)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 11:24 | IP
|
|
Dasha 2009
Новичок
|
Помогите пожайлуста, очень нужно:
Из партии в 1500 штук деталей, из которых 90 "плюсовых", производится выборка (с возвратом) в n = 50 штук. Какова вероятность того, что "плюсовых" деталей окажется m = 0, 1, 2, ...; не более трех; более двух; не менее одной и не более пяти?
(Сообщение отредактировал Dasha 2009 10 нояб. 2009 12:45)
|
Всего сообщений: 13 | Присоединился: ноябрь 2009 | Отправлено: 10 нояб. 2009 11:45 | IP
|
|
RKI
Долгожитель
|
Цитата: Ksenechka написал 9 нояб. 2009 21:41
Предполагается,что случайная величина распределена по нормальному закону. По выборке объёмом n=20 вычислены оценки математического ожидания m*( m*=-2) и дисперсии s(s=0,8).При заданной доверительной вероятности найти предельную ошибку оценки математического ожидания и доверительный интервал при заданной доверительной информации в(в=0,95).Определить,какими будут эти величины,если при выборке объёмом n=40 получены такие же величины оценок.
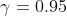
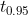 - критическая точка распределения Стьюдента (для двусторонней области) с n-1 = 19 степенями свободы, на уровне значимости 
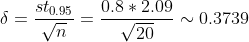
Предельная ошибка равна:
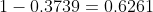
Доверительный интервал:
-----------------------------------------------------------------------------
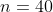
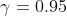
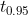- критическая точка распределения Стьюдента (для двусторонней области) с n-1 = 19 степенями свободы, на уровне значимости
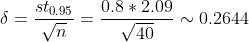
Предельная ошибка равна:
Доверительный интервал:
(Сообщение отредактировал RKI 10 нояб. 2009 12:01)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 нояб. 2009 11:54 | IP
|
|
Ksenechka
Новичок
|
Спасибо Вам огромное Спасибо за то,что Вы есть!
|
Всего сообщений: 4 | Присоединился: ноябрь 2009 | Отправлено: 10 нояб. 2009 12:22 | IP
|
|
|
Форум
Решение задач по теории вероятности
