Yulusik
Новичок
|
    
Помогите пожалуйста с задачей!
3)В партии из 100000 изделий имеется 500 дефектных. Из партии выбирается для контроля 1000 изделий. Найти вероятность того, что среди них будет от 40 до 60 дефектных.
|
Всего сообщений: 21 | Присоединился: сентябрь 2009 | Отправлено: 9 нояб. 2009 18:52 | IP
|
|
SvetYulya
Новичок
|
Спасибо за задачу, насчет первой уточним у преподавателя. Не могли бы Вы решить еще 2 задачи:
1. На 10 одинаковых карточках написано различные числа от 0 до 9. Определить вероятность того, что на удачу образованное с помощью данных карточек трехзначное число делиться на 36.
2.В двух урнах находяться шары, отличающиеся только по цвету, причем в 1ой урне 6 белых, 10 черных и 6 красных шаров, а во второй соответственно 8,8,4. Из обеих урн на удачу извлекаются по одному шару. Какова вероятность,что оба шара разного цвета.
И проверьте пожалуйста вот эти:
1. Вычислить вероятность того, что при бросании двух игральных костей сумма очков на верхних гранях будет больше 10, если разность больше 2.
РЕШЕНИЕ:
A = {сумма очков больше 10}
B = {разность очков больше 2} = {(6;1); (1;6);(6;2);(2;6);(6;3);(3;6);(5;1);(1;5);(5;2);(2;5);(4;1);(1;4)}
|B| = 12
AB = {сумма очков больше 10 и разность очков больше 2}
|AB| = 0
P(A|B) = |AB|/|B| = 0/12 = 0
2. Вероятность выигрыша по одному билету лотереи равна 1/4. Какова вероятность того. Что лицо, имеющее шесть билетов не выиграет по двум билетам.
РЕШЕНИЕ:
A = {не выиграет по двум билетам}
р=1/4
k=2
n=6
q=1-р=1-1/4=3/4
Р(А)=С(2;6)*(1/4)^2*(3/4)^4=15*1/16*81/256=0,29663
3. На трех станках обрабатываются однотипные детали; вероятность брака для станка № 1 составляет 0,06, а для станков № 2 №3 - 0,05. Обработанные детали складываются в одном месте, причем станок № 1 обрабатывает вдвое больше деталей, чем станок № 2 и втрое больше, чем станок №3 . Вычислить вероятность того, что взятая наудачу деталь не будет бракованной.
РЕШЕНИЕ:
H1 = {деталь обработана на первом станке}
H2 = {деталь обработана на втором станке}
H3 = {деталь обработана на третьем станке}
P(H1) = 6/11
P(H2) = 3/11
P(H3) = 2/11
A = {деталь не будет бракованной}
P(A|H1) = 1 - 0.06 = 0.94
P(A|H2) = 1 - 0.05 = 0.95
P(A|H3) = 1 - 0.05 = 0.95
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2)+ P(H3)P(A|H3) =
= (6/11)*(0.94) + (3/11)*(0.95)+ (2/11)*(0.95) = 2.92/3 =
= 10,39/11 = 0,94
4. Корректура в 1000 страниц содержит 500 опечаток, найти вероятность того, что на странице не меньше трех опечаток.
РЕШЕНИЕ:
лямбда = 500/1000 = 0.5
По теореме Пуассона
P(m=0) = ( (0.5^0)/0! )*e^(-1/2) = e^(-1/2) = 0.6065
P(m=1) = ( (0.5^1)/1! )*e^(-1/2) = 0.5*e^(-2) = 0.3033
P(m=2) = ( (0.5^2)/2! )*e^(-1/2) = 0,0758
P(m=3) = ( (0.5^3)/3! )*e^(-1/2) = 0,0126
A = {на странице окажется не меньше трех опечаток}
P(A) = P(m>=3) = 1 - P(m<3) = 1 - P(m=0) - P(m=1)- P(m=2)- P(m=3) = 1-0.6065 - 0.3033- 0,0758-0,0126=0,0018
5. Вероятность неточной сборки прибора равна 0,15. Найти вероятность того, что среди 500
приборов окажется от 400 до 480 (включительно) точных.
РЕШЕНИЕ:
n = 500
p =0,15
q = 1-p =0,85
np = 75
npq = 64
sqrt(npq) = 8
А = {от 400 до 480 точных приборов}
m1 = 400
x1 = (m1 - np)/sqrt(npq) = (400 - 75)/8 = 40,625
m2 = 480
x2 = (m2 - np)/sqrt(npq) = (480 - 75)/8 =50,625
По интегральной теореме Муавра-Лапласа
P(А) = P(m1<=m<=m2) = Ф(x2) - Ф(x1) = Ф(50,625) - Ф(40,625) = 0,5-0,5=0
6.При стрельбе была получена частотность попадания 0,6. Сколько было сделано выстрелов, если получено 12 промахов.
Решение:
W(A)= m/n
W(A)=0,6. m=12. Найдем n.
n= m/W(A) = 12 / 0,6 = 20.
7.Вероятность выживания бактерий после радиоактивного облучения равна 0,004. Найти вероятность того, что после облучения из 500 бактерий останется более трех бактерий.
Решение:
Число n=500 велико, вероятность р=0,004 мала и рассматриваемые события(выживания бактерий) независимы, поэтому имеет место формула Пуассона.
Найдем лямбда:
лямбда = 500/1000 = 0.5
P(m=0) = ( (2^0)/0! )*e^(-2) =e^(-2)~ 0.1353
P(m=1) = (2^1)(e^(-2))/1!=2(e^(-2)) ~ 0.27067
P(m=2) = (2^2)(e^(-2))/2!=4*e^(-2)/2=2(e^(-2)) ~0.27067
P(m=3) = (2^3)(e^(-2))/3!=8*e^(-2)/6=4*e^(-2)/3 ~ 0.1804
A = {выживет более трех бактерий}
P(A) = P(m>3) = 1 - (P(m=0) + P(m=1)+P(m=2) + P(m=3)) =1-(0.1353+0.27067+0.27067+0.1804)=1-0,85704=0,14296
8. Пусть вероятность того, что покупателю необходима обувь 41-го размера, равна 0,2.Найти вероятность того, что из 750 покупателей не более 120 потребуется обувь именно этого размера.
Решение:
По условию
n=750
p=0,2
k1=0
k2=120
Вычислим x' и x'' .
q=0.8
x'= k1-np/ sqrt (npq) = 0-750*0,2/ sqrt(750*0.2*0.8) = -150/spq(120)= -13.7
x''= k2-np/ sqrt (npq)= 120-750*0.2/ sqrt(750*0.2*0.8)= -2.73
Ф(х2)= Ф(-2,73)=-Ф(2,73)=-0,497
Ф(х1)= Ф(-13,7)=-Ф(13,7)=-0,5
Р750(0;120)=-0,497+0,5=0,003
(Сообщение отредактировал SvetYulya 10 нояб. 2009 1:48)
(Сообщение отредактировал SvetYulya 10 нояб. 2009 1:49)
|
Всего сообщений: 11 | Присоединился: ноябрь 2009 | Отправлено: 9 нояб. 2009 19:04 | IP
|
|
malna
Новичок
|
RKI спасибо большое, учту на будущее.
|
Всего сообщений: 8 | Присоединился: ноябрь 2009 | Отправлено: 9 нояб. 2009 19:15 | IP
|
|
Dasha 2009
Новичок
|
Здравствуйте помогите с задачей:
Всхожесть семян данного растения составляет 90%.
Найти вероятность того, что из 1000 посеянных семян взойдет: а) 900; б) не менее 900; в)не более 920; г) не менее 880 и не более 900.
Какие отклонения фактической частоты проросших семян от их вероятности (90%) можно ожидать с уверенностью: а) 95%; б) 99%?
Сколько необходимо взять семян, чтобы с вероятностью 95% можно было утверждать, что отклонение фактической частоты m/n от вероятности 90% не превосходит: а) 2%; б) 3%?
|
Всего сообщений: 13 | Присоединился: ноябрь 2009 | Отправлено: 9 нояб. 2009 19:54 | IP
|
|
RKI 
Долгожитель
|
Цитата: Dasha 2009 написал 9 нояб. 2009 19:54
Всхожесть семян данного растения составляет 90%.
Найти вероятность того, что из 1000 посеянных семян взойдет: а) 900; б) не менее 900; в)не более 920; г) не менее 880 и не более 900.
n = 1000 - количество посеянных семян
p = 0.9 - вероятность всхода одного отдельного семени
q = 1 - p = 1 - 0.9 = 0.1
np = 1000*(0.9) = 900
npq = 1000*(0.9)*(0.1) = 90
m - количество взошедших семян
а)
 \sim \frac{1}{\sqrt{90} } \phi (\frac{900 - 900}{\sqrt{90} }) = \frac{1}{\sqrt{90} } \phi (0) \sim )
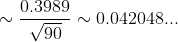
б)
 = 0.5 - \Phi (\frac{900 - 900}{\sqrt{90} }) = 0.5 - \Phi (0) = 0.5 - 0 = 0.5 )
в)
 = 0.5 + \Phi (\frac{920 - 900}{\sqrt{90} }) \sim 0.5 + \Phi (2.11) \sim )
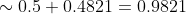
г)
 = \Phi (\frac{900 - 900}{\sqrt{90} }) - \Phi (\frac{880 - 900}{\sqrt{90} }) \sim )
 - \Phi (-2.11) = \Phi (0) + \Phi (2.11) \sim 0 + 0.4821 = 0.4821 )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 нояб. 2009 20:20 | IP
|
|
RKI
Долгожитель
|
Цитата: Dasha 2009 написал 9 нояб. 2009 19:54
Какие отклонения фактической частоты проросших семян от их вероятности (90%) можно ожидать с уверенностью: а) 95%; б) 99%?
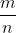 - фактическая частота
n = 1000
p = 0.9
q = 1 - p = 1 - 0.9 = 0.1
 = 2\Phi (\epsilon\sqrt{\frac{n}{pq} }) )
а)
 = 2\Phi(\epsilon\sqrt{\frac{n}{pq} }) = 0.95 )
 = 0.475 )
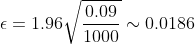
Отклонения равны: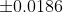 
б)
 = 2\Phi(\epsilon\sqrt{\frac{n}{pq} }) = 0.99 )
 = 0.495 )
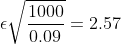
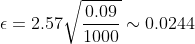
Отклонения равны: 
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 нояб. 2009 20:32 | IP
|
|
RKI
Долгожитель
|
Цитата: Dasha 2009 написал 9 нояб. 2009 19:54
Сколько необходимо взять семян, чтобы с вероятностью 95% можно было утверждать, что отклонение фактической частоты m/n от вероятности 90% не превосходит: а) 2%; б) 3%?
а)
 = 2\Phi (0.02\sqrt{\frac{n}{0.09} }) = 0.95 )
 = 0.475 )
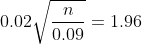
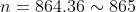
б)
 = 2\Phi (0.03\sqrt{\frac{n}{0.09} }) = 0.95 )
 = 0.475 )
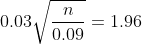
(Сообщение отредактировал RKI 9 нояб. 2009 20:41)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 нояб. 2009 20:41 | IP
|
|
alexs777
Новичок
|
Помогите решить задачки, по теории вероятности, зарание благодарю.
|
Всего сообщений: 6 | Присоединился: ноябрь 2009 | Отправлено: 9 нояб. 2009 21:16 | IP
|
|
Ksenechka
Новичок
|
Добрый вечер Имея филологическое образование,высшую математику мне не потянуть...помогите,пожалуйста Задача: Предполагается,что случайная величина распределена по нормальному закону. По выборке объёмом n=20 вычислены оценки математического ожидания m*( m*=-2) и дисперсии s(s=0,8).При заданной доверительной вероятности найти предельную ошибку оценки математического ожидания и доверительный интервал при заданной доверительной информации в(в=0,95).Определить,какими будут эти величины,если при выборке объёмом n=40 получены такие же величины оценок. Заранее благодарю
(Сообщение отредактировал Ksenechka 9 нояб. 2009 23:01)
|
Всего сообщений: 4 | Присоединился: ноябрь 2009 | Отправлено: 9 нояб. 2009 21:41 | IP
|
|
Dasha 2009
Новичок
|
Спасибо большое
|
Всего сообщений: 13 | Присоединился: ноябрь 2009 | Отправлено: 9 нояб. 2009 22:29 | IP
|
|
|
Форум
Решение задач по теории вероятности
