Karim
Начинающий
|
    
Блин, ну ты КРАСОТКА!
Спасибо!
Наверное эта тема только на тебе, RKI и держисься!
Спасибо...
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 8 нояб. 2009 18:52 | IP
|
|
RKI 
Долгожитель
|
Ну что Вы
Огромную помощь оказывает и ProstoVasya
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 нояб. 2009 19:02 | IP
|
|
tatank4
Новичок
|
Помогите решить задачи по теории вероятности!!!!! пожалуста!!!!! желательно до 10 ноября
1.В коробке из 25 изделий 15 повышенного качества. Наудачу извлекается 3 изделия. Опреде-лить вероятность того, что: а) одно из них повышенного качества; б) все три изделия повы-шенного качества; в) хотя бы одно изделие повышенного качества.
2. Четыре шарика случайным образом разбрасываются по четырем лункам. Каждый шарик с рав-ной вероятностью и независимо от других попадает в любую лунку. Определить вероятность того, что все шарики окажутся в одной из лунок.
3. На отрезке [0, 1] случайным образом выбираются два числа x и y. Определить вероятность то-го, что сумма этих чисел больше 1, а абсолютная величина разности меньше 0,5.
4. Два парохода независимо подходят к одному и тому же причалу. Время прихода обоих паро-ходов равновозможно в течение данных суток. Время стоянки первого парохода один час, а второго - два часа. Какова вероятность, что одному из пароходов придется ожидать освобож-дения причала.
5. Вероятность того, что цель поражена при одном выстреле первым стрелком – 0,21, вторым – 0,1. Первый сделал 2, второй - 5 выстрелов. Определить вероятность того, что цель не пораже-на.
6. Два предприятия выпускают однотипные изделия. Причем второе выпускает 55% всех изде-лий. Вероятность выпуска нестандартного изделия первым предприятием 0,1, вторым 0,15. а) Определить вероятность того, что взятое наудачу изделие окажется не стандартным, б) Взятое изделие оказалось нестандартным. Какова вероятность, что оно выпущено на втором предпри-ятии?
7. Пара игральных костей бросается 20 раз. Определить вероятность того, что сумма очков, рав-ная 12, появилась хотя бы два раза.
8. Вероятность наступления некоторого события в каждом из 700 независимых испытаний равна 0,8. Определить вероятность того, что число m наступлений события удовлетворяет неравенству 545≤m575.
заранее спасибо)))
|
Всего сообщений: 7 | Присоединился: ноябрь 2009 | Отправлено: 8 нояб. 2009 21:17 | IP
|
|
asselka
Новичок
|
Ой! Спасибо вам огромное! =*
А то с логикой у меня плохо =))
|
Всего сообщений: 16 | Присоединился: октябрь 2009 | Отправлено: 8 нояб. 2009 21:56 | IP
|
|
RKI
Долгожитель
|
Цитата: tatank4 написал 8 нояб. 2009 21:17
5. Вероятность того, что цель поражена при одном выстреле первым стрелком – 0,21, вторым – 0,1. Первый сделал 2, второй - 5 выстрелов. Определить вероятность того, что цель не пораже-на.
Ai = {при i-том выстреле первый стрелок попал в мишень}, i=1,2
P(Ai) = 0.21
не Ai = {при i-том выстреле первый стрелок промахнулся}, i=1,2
P(не Ai) = 1 - P(Ai) = 1 - 0.21 = 0.79
Bj = {при j-том выстреле второй стрелок попал в мшень}, j=1,2,3,4,5
P(Bj) = 0.1
не Bj = {при j-том выстреле второй стрелок промахнулся}, j=1,2,3,4,5
P(не Bj) = 1 - P(Bj) = 1 - 0.1 = 0.9
C = {цель не поражена}
C = (не A1)*(не A2)*(не B1)*(не B2)*(не B3)*(не B4)*(не B5)
P(C) =
= P((не A1)*(не A2)*(не B1)*(не B2)*(не B3)*(не B4)*(не B5)) =
= P(не A1)*P(не A2)*P(не B1)*P(не B2)*P(не B3)*P(не B4)*P(не B5) =
= (0.79)*(0.79)*(0.9)*(0.9)*(0.9)*(0.9)*(0.9) =
= 0.368524809
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 нояб. 2009 22:41 | IP
|
|
RKI
Долгожитель
|
Цитата: tatank4 написал 8 нояб. 2009 21:17
6. Два предприятия выпускают однотипные изделия. Причем второе выпускает 55% всех изде-лий. Вероятность выпуска нестандартного изделия первым предприятием 0,1, вторым 0,15. а) Определить вероятность того, что взятое наудачу изделие окажется не стандартным, б) Взятое изделие оказалось нестандартным. Какова вероятность, что оно выпущено на втором предпри-ятии?
H1 = {изделие выпущено на первом предприятии}
H2 = {изделие выпущено на втором предприятии}
P(H2) = 0.55
P(H1) = 1 - P(H2) = 1 - 0.55 = 0.45
A = {изделие нестандартное}
A|H1 = {изделие нестандартное при условии, что оно выпущено первым предприятием}
A|H2 = {изделие нестандартное при условии, что оно выпущено вторым предприятием}
P(A|H1) = 0.1
P(A|H2) = 0.15
а) По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) =
= (0.45)*(0.1) + (0.55)*(0.15) =
= 0.045 + 0.0825 = 0.1275
б) H2|A = {изделие выпущено на втором предприятии при условии, что изделие нестандартное}
По формуле Байеса
P(H2|A) = P(H2)P(A|H2)/P(A) = (0.55)*(0.15)/(0.1275) =
= (0.0825)/(0.1275) = 11/17
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 нояб. 2009 22:49 | IP
|
|
RKI
Долгожитель
|
Цитата: tatank4 написал 8 нояб. 2009 21:17
7. Пара игральных костей бросается 20 раз. Определить вероятность того, что сумма очков, рав-ная 12, появилась хотя бы два раза.
n = 20 - количество бросков
p = 1/36 - вероятность выпадения суммы очков, равной 12
q = 1 - p = 1 - 1/36 = 35/36
m - количество выпадений, при которых сумма очков равна 12
 = 1 - P(m < 2) = 1 - (P(m=0) + P(m=1)) = )
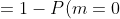 - P(m=1) = 1 - (\frac{35}{36})^{20} - C_{20}^{1}*\frac{1}{36}*(\frac{35}{36})^{19} = )
^{20} - \frac{20}{36}*(\frac{35}{36})^{19} = )
^{19}*(\frac{35}{36} - \frac{20}{36}) = )
^{19} = )
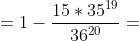
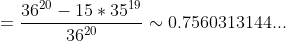
P.S. Использовалась формулла Бернулли
(Сообщение отредактировал RKI 8 нояб. 2009 23:08)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 нояб. 2009 23:01 | IP
|
|
RKI
Долгожитель
|
Цитата: tatank4 написал 8 нояб. 2009 21:17
8. Вероятность наступления некоторого события в каждом из 700 независимых испытаний равна 0,8. Определить вероятность того, что число m наступлений события удовлетворяет неравенству 545≤m575.
Отредактируйте Ваше сообщение.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 нояб. 2009 23:05 | IP
|
|
RKI
Долгожитель
|
Цитата: tatank4 написал 8 нояб. 2009 21:17
4. Два парохода независимо подходят к одному и тому же причалу. Время прихода обоих паро-ходов равновозможно в течение данных суток. Время стоянки первого парохода один час, а второго - два часа. Какова вероятность, что одному из пароходов придется ожидать освобож-дения причала.
Ваша задача практически была решена здесь
http://exir.ru/cgi-bin/ikonboard/topic.cgi?forum=7&topic=2182&start=250
пример 240
В Вашей задаче необходимо вычислить вероятность события
B = {одному из пароходов придется ожидать освобождения причала}
B = не A
P(B) = P(не A) = 1 - P(A) = 1 - 253/288 = 35/288
P.S. Данная задача на тему геометрическая вероятность. Поэтому необходимо сделать соответствующие рисунки.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 нояб. 2009 23:13 | IP
|
|
RKI
Долгожитель
|
Цитата: tatank4 написал 8 нояб. 2009 21:17
1.В коробке из 25 изделий 15 повышенного качества. Наудачу извлекается 3 изделия. Опреде-лить вероятность того, что: а) одно из них повышенного качества; б) все три изделия повы-шенного качества; в) хотя бы одно изделие повышенного качества.
Посчитаем число n всевозможных исходов. Способов выбрать 3 изделия из 25 имеющихся
n = C(3;25) = 25!/3!22! = 2300
а) A = {одно изделие повышенного качества}
Посчитаем число l исходов, благоприятных событию A. Способов выбрать 1 изделие повышенного качества из 15 имеющихся
l1 = C(1;15) = 15!/1!14! = 15.
Способов выбрать 2 изделия нормального качества из 10 имеющихся
l2 = C(2;10) = 10!/2!8! = 45.
По правилу произведения l = l1*l2 = 15*45 = 675
По классическому определению вероятности
P(A) = l/n = 675/2300 = 27/92
б) B = {3 изделия повышенного качества}
Посчитаем число k исходов, благоприятных событию B. Способов выбрать 3 изделия повышенного качества из 15 имеющихся
k = C(3;15) = 15!/3!12! = 455
По классическому определению вероятности
P(B) = k/n = 455/2300 = 91/460
в) C = {хотя бы одно изделие повышенного качества}
не C = {все 3 изделия нормального качества}
Посчитаем число m исходов, благоприятных событию не C. Способов выбрать 3 изделия нормального качества из 10 имеющихся
m = C(3;10) = 10!/3!7! = 120
По классическому определению вероятности
P(не C) = m/n = 120/2300 = 6/115
P(C) = 1 - P(не C) = 1 - 6/115 = 109/115
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 9 нояб. 2009 9:49 | IP
|
|
|
Форум
Решение задач по теории вероятности
