Snigur
Новичок
|
   
Огромное спасибо, никогда бы такое не решил!
помогите пожалуйста еще с одной задачей:
Среди партии полученных строительной фирмой намеки попадаются бракованные с вероятностью 0,05. В течении недели фирма получила 500 панелей. Какова вероятность того, что среди них качественных оказалось:
а) менее 450
б) более 490
в) менее 480, но более 460.
|
Всего сообщений: 19 | Присоединился: июль 2009 | Отправлено: 8 нояб. 2009 17:06 | IP
|
|
RKI 
Долгожитель
|
Цитата: Karim написал 8 нояб. 2009 16:55
Задача 10.
В цеху 3 независимо работающих линии. Вероятность того, что в случайный момент времени загружены 1-я линия-0,9, 2-я-0,8, 3-я - 0,7. Найти вероятность того, что в случайный момент времени:
а)загружены 2 линии,
б)хотя бы одна линия свободна,
в) две линии свободны.
перечитал все ваши типовые задачи, но оставшиеся я там не нашел...
Приятно, что мои типовые задачи читаются 
Ai = {загружена i-тая линия}, i = 1,2,3
P(A1) = 0.9
P(A2) = 0.8
P(A3) = 0.7
не Ai = {i-тая линия свободна}, i = 1,2,3
P(не A1) = 1 - P(A1) = 1 - 0.9 = 0.1
P(не A2) = 1 - P(A2) = 1 - 0.8 = 0.2
P(не A3) = 1 - P(A3) = 1 - 0.7 = 0.3
а) A = {2 линии загружены}
A = A1*A2*(не A3) + A1*(не A2)*A3 + (не A1)*A2*A3
P(A) =
= P(A1*A2*(не A3) + A1*(не A2)*A3 + (не A1)*A2*A3) =
= P(A1*A2*(не A3)) + P(A1*(не A2)*A3) + P((не A1)*A2*A3) =
= P(A1)P(A2)P(не A3) + P(A1)P(не A2)P(A3) + P(не A1)P(A2)P(A3) =
= (0.9)*(0.8)*(0.3) + (0.9)*(0.2)*(0.7) + (0.1)*(0.8)*(0.7) =
= 0.216 + 0.126 + 0.056 =
= 0.398
б) B = {хотя бы одна линия свободна}
не B = {все линии заняты}
не B = A1*A2*A3
P(не B) = P(A1*A2*A3) = P(A1)*P(A2)*P(A3) =
= (0.9)*(0.8)*(0.7) = 0.504
P(B) = 1 - P(не B) = 1 - 0.504 = 0.496
в) C = {2 линии свободны}
С = (не A1)*(не A2)*A3 + (не A1)*A2*(не A3) + A1*(не A2)*(не A3)
P(C) =
= P((не A1)*(не A2)*A3 + (не A1)*A2*(не A3) + A1*(не A2)*(не A3)) =
= P((не A1)*(не A2)*A3) + P((не A1)*A2*(не A3)) + P(A1*(не A2)*(не A3)) =
= P(не A1)*P(не A2)*P(A3) + P(не A1)*P(A2)*P(не A3) + P(A1)P(не A2)P(не A3) =
= (0.1)*(0.2)*(0.7) + (0.1)*(0.8)*(0.3) + (0.9)*(0.2)*(0.3) =
= 0.014 + 0.024 + 0.054 =
= 0.092
P.S.
На форуме для удобства я использую запись (не A). Но правильно писать
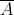
(Сообщение отредактировал RKI 8 нояб. 2009 17:21)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 нояб. 2009 17:20 | IP
|
|
RKI
Долгожитель
|
Цитата: Snigur написал 8 нояб. 2009 17:06
Среди партии полученных строительной фирмой намеки попадаются бракованные с вероятностью 0,05. В течении недели фирма получила 500 панелей. Какова вероятность того, что среди них качественных оказалось:
а) менее 450
б) более 490
в) менее 480, но более 460.
n = 500 - общее количество панелей
q = 0.05 - вероятность того, что панель бракованная
p = 1 - q = 1 - 0.05 = 0.95 - вероятность того, что панель качественная
np = 500*(0.95) = 475
npq = 500*(0.95)*(0.05) = 23.75
m - количество качественных панелей
а)
 = 0.5 + \Phi (\frac{450 - 475}{\sqrt{23.75} }) \sim 0.5 + \Phi (- 5.13) = )
 \sim 0.5 - 0.5 = 0 )
б)
 = 0.5 - \Phi (\frac{490 - 475}{\sqrt{23.75} }) \sim 0.5 - \Phi (3.08) \sim )
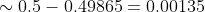
в)
 = \Phi (\frac{480 - 475}{\sqrt{23.75} }) - \Phi (\frac{460 - 475}{\sqrt{23.75} }) \sim )
 - \Phi (-3.08) = \Phi (1.03) + \Phi (3.08) \sim 0.3485 + 0.49865 = 0.84715 )
Использовалась интегральная теорема Муавра-Лапласа
(Сообщение отредактировал RKI 8 нояб. 2009 17:48)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 нояб. 2009 17:46 | IP
|
|
Karim
Начинающий
|
У меня осталось еще 2 задачки! Можно? Одна вообще легкая, но я не знаю, как выразить, и вторая не сложная, но что то не соображу! Можно? Посмотрите?
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 8 нояб. 2009 18:02 | IP
|
|
RKI
Долгожитель
|
Цитата: Karim написал 8 нояб. 2009 18:02
У меня осталось еще 2 задачки! Можно? Одна вообще легкая, но я не знаю, как выразить, и вторая не сложная, но что то не соображу! Можно? Посмотрите?
можно
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 нояб. 2009 18:03 | IP
|
|
Karim
Начинающий
|
Задача 11.
Производятся 3 испытания прибора. Аi-событие, состоящее в том, что при i-ом испытании (i=1, 2, 3) прибор выйдет из строя. Выразить через Аi следующие события:
а) прибор выйдет из строя при 2-х испытаниях;
б) прибор не выйдет из строя;
в) прибор выйдет из строя хотя бы при одном испытании.
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 8 нояб. 2009 18:23 | IP
|
|
Karim
Начинающий
|
Задача 12.
В магазин поступили пылесосы двух фирм Bоsh и Indеsit в соотношении 30% и 70%. Вероятность брака равна соответственно 0,05 и 0,01. Покупатель наудачу выбирает качественный пылесос. Найти вероятность того, что пылесос оказался фирмы Воsh.
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 8 нояб. 2009 18:28 | IP
|
|
Snigur
Новичок
|
Огромное, огромное спасибо тебе, RKI. Ты меня выручила. Спасибо. Спасибо. Спасибо!
|
Всего сообщений: 19 | Присоединился: июль 2009 | Отправлено: 8 нояб. 2009 18:35 | IP
|
|
RKI
Долгожитель
|
Цитата: Karim написал 8 нояб. 2009 18:23
Задача 11.
Производятся 3 испытания прибора. Аi-событие, состоящее в том, что при i-ом испытании (i=1, 2, 3) прибор выйдет из строя. Выразить через Аi следующие события:
а) прибор выйдет из строя при 2-х испытаниях;
б) прибор не выйдет из строя;
в) прибор выйдет из строя хотя бы при одном испытании.
а)
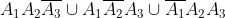
б)
в)
(Сообщение отредактировал RKI 8 нояб. 2009 18:36)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 нояб. 2009 18:35 | IP
|
|
RKI
Долгожитель
|
Цитата: Karim написал 8 нояб. 2009 18:28
Задача 12.
В магазин поступили пылесосы двух фирм Bоsh и Indеsit в соотношении 30% и 70%. Вероятность брака равна соответственно 0,05 и 0,01. Покупатель наудачу выбирает качественный пылесос. Найти вероятность того, что пылесос оказался фирмы Воsh.
H1 = {пылесос фирмы Bosh}
H2 = {пылесос фирмы Indesit}
P(H1) = 0.3
P(H2) = 0.7
A = {качественный пылесос}
A|H1 = {пылесос качественный при условии, что он фирмы Bosh}
A|H2 = {пылесос качественный при условии, что он фирмы Indesit}
P(A|H1) = 1 - 0.05 = 0.95
P(A|H2) = 1 - 0.01 = 0.99
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) =
= (0.3)*(0.95) + (0.7)*(0.99) =
= 0.285 + 0.693 = 0.978
H1|A = {пылесос фирмы Bosh при условии, что пылесос качественный}
По формуле Байеса
P(H1|A) = P(H1)P(A|H1)/P(A) = (0.3)*(0.95)/(0.978) =
= (0.285)/(0.978) = 95/326
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 нояб. 2009 18:43 | IP
|
|
|
Форум
Решение задач по теории вероятности
