RKI 
Долгожитель
|
   
Цитата: Kremniy написал 7 нояб. 2009 17:23
Вечер добрый всем.
Кто сможет подсказать решение моей задачи?
Или может за деньги кто подскажет? Задача сложная.
Задан закон распределения двумерной дискретной случайной величины (X,Y)
X \ Y_____ 0____1_____2 ____3
-1______0.02__0.03__0,09__0.01
0______0,04__0,20__0,16__0.10
1______0,05__0.10__0,15__0.05
Найти: а) законы распределения одномерных случайных величин X и Y; б) условные законы распределения случайной величины X при условии Y= 2 и случайной величины Y при условии X = 1; в) вероятность P(Y > X).
в)
P(Y > X) =
= P(X=-1, Y=0) + P(X=-1, Y=1) + P(X=-1, Y=2) + P(X=-1, Y=3) +
+ P(X=0, Y=1) + P(X=0, Y=2) + P(X=0, Y=3) + P(X=1, Y=2) +
+ P(X=1, Y=3) =
= 0.02 + 0.03 + 0.09 + 0.01 + 0.20 + 0.16 + 0.10 + 0.15 + 0.05 =
= 0.81
ИЛИ
P(Y > X) = 1 - P(Y <= X) =
= 1 - P(X=0, Y=0) - P(X=1, Y=0) - P(X=1, Y=1) =
= 1 - 0.04 - 0.05 - 0.10 = 0.81
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 17:49 | IP
|
|
RKI
Долгожитель
|
Цитата: Kremniy написал 7 нояб. 2009 17:47
Karim, на сколько я знаю, тут можно решить по ф-ле гипер вероятности.
RKI, как я могу вас отблагодарить?
Просто Ваше спасибо
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 17:50 | IP
|
|
Kremniy
Новичок
|
PK,L(k,l)=CkK*ClL/CK+L k+l
K= 7 не бракованные детали
L = 2 - бракованные
k=2 - из извлеченных 3-х деталей 2 НЕ бракованные
l=1 - из извлеченных 3-х деталей 1 бракованная
|
Всего сообщений: 5 | Присоединился: ноябрь 2009 | Отправлено: 7 нояб. 2009 17:53 | IP
|
|
Kremniy
Новичок
|
Огромное моё Вам спасибо. Мне кажется, что такие знания и помощь должны хоть как-то вознаграждаться. Еще раз спасибо.
|
Всего сообщений: 5 | Присоединился: ноябрь 2009 | Отправлено: 7 нояб. 2009 17:56 | IP
|
|
RKI
Долгожитель
|
Цитата: Karim написал 7 нояб. 2009 17:42
Спасибо, еще раз... :-)
задача 7.
В ящике имеется 9 деталей, среди которых 2 бракованные. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что:
а) извлеченные детали качественные,
б) среди извлеченных деталей 1 бракованная.
решение:
а) m(А)=7!/(7-3)!3!=35-число исходов, благоприятствующих наступлению событию А.
n=9!/(9-3)!3!=84-общее число возможных исходов.
Р(А)=m(А)/n=35/84=0,42.
б) а вот это не могу сообразить, подскажите хотя бы формулу.
А первое правильно?
Первое правильно
б) B = {1 бракованная деталь и 2 стандартные детали}
Способов извлечь 1 бракованную деталь из 2 имеющихся
m1 = C(1;2) = 2!/1!1! = 2.
Способов извлечь 2 стандартные детали из 7 имеющихся
m2 = C(2;7) = 7!/2!5! = 21
m(B) = m1*m2 = 2*21 = 42
P(B) = m(B)/n = 42/84 = 0.5
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 18:00 | IP
|
|
Tiffany
Новичок
|
Спасибо 
Помогите еще с 2 задачками, если не сложно...
1. Вероятность "сбоя" в работе телефонной станции при каждом вызове равна 0,004. Поступило 500 вызовов. Определить вероятность что при этом будет не более 6 "сбоев"
2. Вероятность наступления некоторого события в каждом из 100 независимых испытаний равна 0,8. Определить вероятность того, что число m наступлений события удовлетворяет неравенству 85<=m<=95
|
Всего сообщений: 4 | Присоединился: ноябрь 2009 | Отправлено: 7 нояб. 2009 18:01 | IP
|
|
RKI
Долгожитель
|
Цитата: Tiffany написал 7 нояб. 2009 18:01
1. Вероятность "сбоя" в работе телефонной станции при каждом вызове равна 0,004. Поступило 500 вызовов. Определить вероятность что при этом будет не более 6 "сбоев"
n = 500 - количество вызовов
p = 0.004 - вероятность сбоя при отдельно взятом вызове
np = 500*(0.004) = 2
m - общее количество сбоев
 = P(m=0) + P(m=1) + P(m=2) + P(m=3) + P(m=4) + P(m=5) + P(m=6) = )
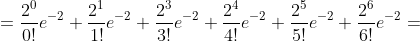
e^{-2} = )
|
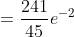
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 19:17 | IP
|
|
RKI
Долгожитель
|
Цитата: Tiffany написал 7 нояб. 2009 18:01
2. Вероятность наступления некоторого события в каждом из 100 независимых испытаний равна 0,8. Определить вероятность того, что число m наступлений события удовлетворяет неравенству 85<=m<=95
n = 100
p = 0.8
q = 1 - p = 1 - 0.8 = 0.2
np = 100*(0.8) = 80
npq = 100*(0.8)*(0.2) = 16
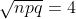
 = \Phi (\frac{95 - 80}{4}) - \Phi (\frac{85 - 80}{4}) = \Phi (3.75) - \Phi (1.25) \sim )
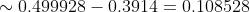
(Сообщение отредактировал RKI 7 нояб. 2009 19:22)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 19:22 | IP
|
|
Kremniy
Новичок
|
Помогите, если не сложно, еще с одной задачкой:
Два игрока А и В поочередно бросают монету. Выигравшим считается тот, у кого раньше выпадает герб. Первый бросок делает игрок А , второй бросок -В, третий -А и т. д. Найти вероятность того, что выиграл А не позднее 12-го броска.
|
Всего сообщений: 5 | Присоединился: ноябрь 2009 | Отправлено: 7 нояб. 2009 19:24 | IP
|
|
Ulenka20
Новичок
|
Здравствуйте, снова вынуждена обратиться к вам с просьбой помочь в решении задачи.
На фирме работают 8 аудиторов, из которых 3 - высокой квалификации, и 5 программистов, из которых 2 - высокой квалификации. В командировку надо отправить группу из 3 аудиторов и 2 программистов. Какова вероятность того, что в этой группе окажется по крайней мере 1 аудитор высокой квалификации и хотя бы 1 программист высокой квалификации, если каждый специалист имеет равные возможности поехать в командировку?
|
Всего сообщений: 16 | Присоединился: ноябрь 2009 | Отправлено: 7 нояб. 2009 19:30 | IP
|
|
|
Форум
Решение задач по теории вероятности
