M a s h a
Новичок
|
   
Огромное-преогромное ВАМ спасибо, RKI! Как хорошо, что есть такие люди как вы! СПАСИБО!
|
Всего сообщений: 6 | Присоединился: ноябрь 2009 | Отправлено: 7 нояб. 2009 16:29 | IP
|
|
Tiffany
Новичок
|
Здравствуйте  Помогите пожалуйста задачку решить....
В альбоме 7 чистых и 6 гашеных марок. Из них наудачу извлекают 2 марки, подвергаются спецгашению и возвращаются в альбом. После этого вновь наудачу извлекаются 3 марки. Определить вероятность того, что все они чистые.
|
Всего сообщений: 4 | Присоединился: ноябрь 2009 | Отправлено: 7 нояб. 2009 16:49 | IP
|
|
Karim
Начинающий
|
Задача 6.
Вот эту как решить я вообще не знаю!
СВ Х распределена по нормальному закону с плотностью
f(х)=(1/(sqrt(2П))*е^(-(х+1)^2/2).
Найти Р(-1<х<3), Р(2<=х<=4).
Помогите пожалуйста
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 7 нояб. 2009 16:55 | IP
|
|
RKI 
Долгожитель
|
Цитата: Tiffany написал 7 нояб. 2009 16:49
В альбоме 7 чистых и 6 гашеных марок. Из них наудачу извлекают 2 марки, подвергаются спецгашению и возвращаются в альбом. После этого вновь наудачу извлекаются 3 марки. Определить вероятность того, что все они чистые.
H1 = {достали 2 чистые марки для спецгашения}
H2 = {достали 2 гашеные марки}
H3 = {достали 1 чистую и 1 гашеную марку}
P(H1) = C(2;7)/C(2;13) = 21/78 = 7/26
P(H2) = C(2;6)/C(2;13) = 15/78 = 5/26
P(H3) = C(1;7)C(1;6)/C(2;13) = 42/78 = 14/26
A = {второй раз достали 3 чистые марки}
A|H1 = {достали 3 чистые марки, если в альбоме 5 чистых и 8 гашеных марок}
A|H2 = {достали 3 чистые марки, если в альбоме 7 чистых и 6 гашеных марок}
A|H3 = {достали 3 чистые марки, если в альбоме 6 чистых и 7 гашеных марок}
P(A|H1) = C(3;5)/C(3;13) = 10/286
P(A|H2) = C(3;7)/C(3;13) = 35/286
P(A|H3) = C(3;6)/C(3;13) = 20/286
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) + P(H3)P(A|H3) =
= (7/26)*(10/286) + (5/26)*(35/286) + (14/26)*(20/286) =
= 70/7436 + 175/7436 + 280/7436 = 525/7436
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 17:02 | IP
|
|
RKI
Долгожитель
|
Цитата: Karim написал 7 нояб. 2009 16:55
Задача 6.
Вот эту как решить я вообще не знаю!
СВ Х распределена по нормальному закону с плотностью
f(х)=(1/(sqrt(2П))*е^(-(х+1)^2/2).
Найти Р(-1<х<3), Р(2<=х<=4).
Помогите пожалуйста
Нормальный закон распределения в общем случае имеет вид:
 = \frac{1}{\sigma\sqrt{2\pi} }e^{-\frac{(x-a)^{2} }{2\sigma^{2} } } )
Таким образом, в нашем случае
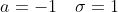
 = \Phi (\frac{3 - a}{\sigma}) - \Phi (\frac{-1 - a}{\sigma}) = )
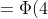 - \Phi (0) \sim 0.499968 - 0 = 0.499968 )
 = \Phi (\frac{4 - a}{\sigma}) - \Phi (\frac{2 - a}{\sigma}) = )
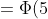 - \Phi (3) \sim 0.49999997 - 0.49865 = 0.00134997 )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 17:13 | IP
|
|
Kremniy
Новичок
|
Вечер добрый всем.
Кто сможет подсказать решение моей задачи?
Или может за деньги кто подскажет? Задача сложная.
Задан закон распределения двумерной дискретной случайной величины (X,Y)
X \ Y_____ 0____1_____2 ____3
-1______0.02__0.03__0,09__0.01
0______0,04__0,20__0,16__0.10
1______0,05__0.10__0,15__0.05
Найти: а) законы распределения одномерных случайных величин X и Y; б) условные законы распределения случайной величины X при условии Y= 2 и случайной величины Y при условии X = 1; в) вероятность P(Y > X).
(Сообщение отредактировал Kremniy 7 нояб. 2009 18:27)
|
Всего сообщений: 5 | Присоединился: ноябрь 2009 | Отправлено: 7 нояб. 2009 17:23 | IP
|
|
RKI
Долгожитель
|
Цитата: Kremniy написал 7 нояб. 2009 17:23
Вечер добрый всем.
Кто сможет подсказать решение моей задачи?
Или может за деньги кто подскажет? Задача сложная.
Задан закон распределения двумерной дискретной случайной величины (X,Y)
X \ Y_____ 0____1_____2 ____3
-1______0.02__0.03__0,09__0.01
0______0,04__0,20__0,16__0.10
1______0,05__0.10__0,15__0.05
Найти: а) законы распределения одномерных случайных величин X и Y; б) условные законы распределения случайной величины X при условии Y= 2 и случайной величины Y при условии X = 1; в) вероятность P(Y > X).
а) P(X = -1) =
= P(X=-1, Y=0) + P(X=-1, Y=1) + P(X=-1, Y=2) + P(X=-1, Y=3) =
= 0.02 + 0.03 + 0.09 + 0.01 = 0.15
P(X = 0) =
= P(X=0, Y=0) + P(X=0, Y=1) + P(X=0, Y=2) + P(X=0, Y=3) =
= 0.04 + 0.20 + 0.16 + 0.10 = 0.50
P(X = 1) =
= P(X=1, Y=0) + P(X=1, Y=1) + P(X=1, Y=2) + P(X=1, Y=3) =
= 0.05 + 0.10 + 0.15 + 0.05 = 0.35
Закон распределения случайной величины X имеет вид:
X -1 0 1
P 0.15 0.50 0.35
P(Y = 0) = P(X=-1, Y=0) + P(X=0, Y=0) + P(X=1, Y=0) =
= 0.02 + 0.04 + 0.05 = 0.11
P(Y = 1) = P(X=-1, Y=1) + P(X=0, Y=1) + P(X=1, Y=1) =
= 0.03 + 0.20 + 0.10 = 0.33
P(Y = 2) = P(X=-1, Y=2) + P(X=0, Y=2) + P(X=1, Y=2) =
= 0.09 + 0.16 + 0.15 = 0.40
P(Y = 3) = P(X=-1, Y=3) + P(X=0, Y=3) + P(X=1, Y=3) =
= 0.01 + 0.10 + 0.05 = 0.16
Закон распределения случайной величины Y имеет вид:
Y 0 1 2 3
P 0.11 0.33 0.40 0.16
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 17:34 | IP
|
|
RKI
Долгожитель
|
Цитата: Kremniy написал 7 нояб. 2009 17:23
Вечер добрый всем.
Кто сможет подсказать решение моей задачи?
Или может за деньги кто подскажет? Задача сложная.
Задан закон распределения двумерной дискретной случайной величины (X,Y)
X \ Y_____ 0____1_____2 ____3
-1______0.02__0.03__0,09__0.01
0______0,04__0,20__0,16__0.10
1______0,05__0.10__0,15__0.05
Найти: а) законы распределения одномерных случайных величин X и Y; б) условные законы распределения случайной величины X при условии Y= 2 и случайной величины Y при условии X = 1; в) вероятность P(Y > X).
б) P(X=-1|Y=2) = P(X=-1, Y=2)/P(Y=2) = (0.09)/(0.40) = 0.225
P(X=0|Y=2) = P(X=0, Y=2)/P(Y=2) = (0.16)/(0.40) = 0.4
P(X=1|Y=2) = P(X=1, Y=2)/P(Y=2) = (0.15)/(0.40) = 0.375
Условный закон распределения случайной величины X при условии Y=2 имеет вид:
X|Y=2 -1 0 1
P 0.225 0.4 0.375
P(Y=0|X=1) = P(X=1, Y=0)/P(X=1) = (0.05)/(0.35) = 1/7
P(Y=1|X=1) = P(X=1, Y=1)/P(X=1) = (0.10)/(0.35) = 2/7
P(Y=2|X=1) = P(X=1, Y=2)/P(X=1) = (0.15)/(0.35) = 3/7
P(Y=3|X=1) = P(X=1, Y=3)/P(X=1) = (0.05)/(0.35) = 1/7
Условный закон распределения случайной величины Y при условии X=1 имеет вид:
Y|X=1 0 1 2 3
P 1/7 2/7 3/7 1/7
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 17:41 | IP
|
|
Karim
Начинающий
|
Спасибо, еще раз... :-)
задача 7.
В ящике имеется 9 деталей, среди которых 2 бракованные. Сборщик наудачу извлекает 3 детали. Найти вероятность того, что:
а) извлеченные детали качественные,
б) среди извлеченных деталей 1 бракованная.
решение:
а) m(А)=7!/(7-3)!3!=35-число исходов, благоприятствующих наступлению событию А.
n=9!/(9-3)!3!=84-общее число возможных исходов.
Р(А)=m(А)/n=35/84=0,42.
б) а вот это не могу сообразить, подскажите хотя бы формулу.
А первое правильно?
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 7 нояб. 2009 17:42 | IP
|
|
Kremniy
Новичок
|
Karim, на сколько я знаю, тут можно решить по ф-ле гипер вероятности.
RKI, как я могу вас отблагодарить?
|
Всего сообщений: 5 | Присоединился: ноябрь 2009 | Отправлено: 7 нояб. 2009 17:47 | IP
|
|
|
Форум
Решение задач по теории вероятности
