natashka1
Новичок
|
   
Кто скажет как решать или решит задачу? В понедельник здавать, уже неделю бьюсь с ней...((
Непрерывная случайная величена задана своей плотностью распеделения:
0, при х<0
F(x) Acos4x при х [0, pi/24]
0 при х>pi/24
Найдите коэффициент А, математическое ожидание, дисперсию случайной величены и вероятность попадания случайной величены в интервал (pi/96, pi/48).
Плиз, ответте
(Сообщение отредактировал natashka1 6 нояб. 2009 21:24)
|
Всего сообщений: 3 | Присоединился: ноябрь 2009 | Отправлено: 6 нояб. 2009 20:55 | IP
|
|
natashka1
Новичок
|
Неужели мне никто не поможет? Спасиииитееее!
|
Всего сообщений: 3 | Присоединился: ноябрь 2009 | Отправлено: 6 нояб. 2009 21:22 | IP
|
|
RKI 
Долгожитель
|
Цитата: natashka1 написал 6 нояб. 2009 20:55
Кто скажет как решать или решит задачу? В понедельник здавать, уже неделю бьюсь с ней...((
Непрерывная случайная величена задана своей плотностью распеделения:
0, при х<0
F(x) Acos4x при х [0, pi/24]
0 при х>pi/24
Найдите коэффициент А, математическое ожидание, дисперсию случайной величены и вероятность попадания случайной величены в интервал (pi/96, pi/48).
f(x) = {0, x < 0
{Acos4x, 0 <= x <= П/24
{0, x > П/24
1) коэффициент A
dx = 1 )
dx = \int\limits_{-\infty}^{0} f(x)dx + \int\limits_{0}^{\frac{\pi}{24} } f(x)dx + \int\limits_{\frac{\pi}{24} }^{+\infty} f(x)dx = )
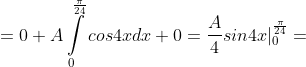
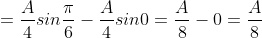
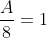
f(x) = {0, x < 0
{8cos4x, 0 <= x <= П/24
{0, x > П/24
2) математическое ожидание
 = \int\limits_{-\infty}^{+\infty} xf(x)dx = )
dx + \int\limits_{0}^{\frac{\pi}{24} } xf(x)dx + \int\limits_{\frac{\pi}{24} }^{+\infty} xf(x)dx = )
dx + \int\limits_{\frac{\pi}{24} }^{+\infty} 0dx = )
dx + 0 = 2\int\limits_{0}^{\frac{\pi}{24} } xd(sin4x) = )
 |_{0}^{\frac{\pi}{24} } - 2\int\limits_{0}^{\frac{\pi}{24} } sin4xdx = )
 = \frac{\pi + 6\sqrt{3} - 12}{24} )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 12:12 | IP
|
|
RKI
Долгожитель
|
Цитата: natashka1 написал 6 нояб. 2009 20:55
Непрерывная случайная величена задана своей плотностью распеделения:
0, при х<0
F(x) Acos4x при х [0, pi/24]
0 при х>pi/24
Найдите коэффициент А, математическое ожидание, дисперсию случайной величены и вероятность попадания случайной величены в интервал (pi/96, pi/48).
3) дисперсия
 = \int\limits_{-\infty}^{+\infty} x^{2}f(x)dx = )
dx + \int\limits_{0}^{\frac{\pi}{24} } x^{2}f(x)dx + \int\limits_{\frac{\pi}{24} }^{+\infty} x^{2}f(x)dx = )
dx + \int\limits_{\frac{\pi}{24} }^{+\infty} 0dx = )
 + 0 = )
d(x^{2}) = )
dx = )
 = )
 |_{0}^{\frac{\pi}{24} } - \int\limits_{0}^{\frac{\pi}{24} } (cos4x)dx = )
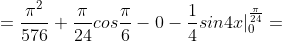
 = \frac{\pi^{2} }{576} + \frac{\sqrt{3}\pi}{48} - \frac{1}{8} )
 = M(X^{2}) - M^{2}(X) = )
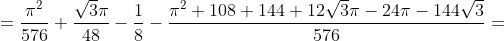
4) вероятность
 = \int\limits_{\frac{\pi}{96} }^{\frac{\pi}{48} } f(x)dx = )
dx = 2sin4x |_{\frac{\pi}{96} }^{\frac{\pi}{48} } = )
|
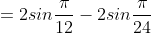
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 12:49 | IP
|
|
malna
Новичок
|
Здравствуйте. Если возможно, помогите решить задачу, что-то я совсем запуталась.
Брошены две игральные кости. Событие А= выпадение шестёрки на первой кости. Событие В=сумма выпавших очков равна7. Являются ли события А и В независимы?
И ещё, правильно я решила следующую задачу?
Случайным образом выбирается число из множества(1,2,3,4,5,6,7,8). Какова вероятность, что: а)оно чётно; б)чётное и делится на 4?
Решение:
а)Р(А)=4/8=0,5
б)m=2, т.к. только 4 и 8 благоприятствуют событию
n=8
Р(А)=2/8=1/4.
Заранее благодарна Вам.
|
Всего сообщений: 8 | Присоединился: ноябрь 2009 | Отправлено: 7 нояб. 2009 14:23 | IP
|
|
RKI
Долгожитель
|
Цитата: malna написал 7 нояб. 2009 14:23
Брошены две игральные кости. Событие А= выпадение шестёрки на первой кости. Событие В=сумма выпавших очков равна7. Являются ли события А и В независимы?
A = {выпадение 6 на первой кости}
P(A) = 1/6
B = {сумма выпавших очков равна 7} = {16; 25; 34; 43; 52; 61}
P(B) = 6/36 = 1/6
AB = {выпадение 6 на первой кости и сумма выпавших очков равна 7} = {61}
P(AB) = 1/36
P(AB) = 1/36 = (1/6)*(1/6) = P(A)*P(B)
Следовательно, события A и B независимы
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 14:52 | IP
|
|
Karim
Начинающий
|
Спасибо, RKI.
задача 5.
Дана функция распределения
{0, х<=-2
F(х)={х/4+1/2, -2<=х<=2
{1, х>2
найти М(Х), f(х), Р(-1<=х<=3).
Решение.
Найдем плотность распределения случайной величины
{0, х<=-2
f(х)=F'(х)={(х/4+1/2)'=1/4, -2<=х<=2
{1, х>2
М(х)=int_{-бесконечность}^{+бесконечность} хf(х)dx=int_{-2}^{2} х*1/4 dх=0
Р(-1<=х<=3)=F(-1)-F(3)=-1/4+1/2(3/4+1/2)=-1.
Правильное решение? Хотя мне кажется, что слишком легко у меня все получилось! Проверьте пожалуйста!
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 7 нояб. 2009 14:53 | IP
|
|
RKI
Долгожитель
|
Цитата: malna написал 7 нояб. 2009 14:23
И ещё, правильно я решила следующую задачу?
Случайным образом выбирается число из множества(1,2,3,4,5,6,7,8). Какова вероятность, что: а)оно чётно; б)чётное и делится на 4?
Решение:
а)Р(А)=4/8=0,5
б)m=2, т.к. только 4 и 8 благоприятствуют событию
n=8
Р(А)=2/8=1/4.
правильно
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 14:54 | IP
|
|
RKI
Долгожитель
|
Цитата: Karim написал 7 нояб. 2009 14:53
задача 5.
Дана функция распределения
{0, х<=-2
F(х)={х/4+1/2, -2<=х<=2
{1, х>2
найти М(Х), f(х), Р(-1<=х<=3).
Решение.
Найдем плотность распределения случайной величины
{0, х<=-2
f(х)=F'(х)={(х/4+1/2)'=1/4, -2<=х<=2
{1, х>2
f(x) = {0, x < -2
{1/4, - 2 < x < 2
{0, x > 2
В точках x = -2 и x = 2 производная F'(x) не существует.
М(х)=int_{-бесконечность}^{+бесконечность} хf(х)dx=int_{-2}^{2} х*1/4 dх=0
Верно
Р(-1<=х<=3)=F(-1)-F(3)=-1/4+1/2(3/4+1/2)=-1.
P(-1 <= X <= 3) = F(3) - F(-1) = 1 - 1/4 = 3/4
Вероятность НИКОГДА не может быть отрицательным числом ИЛИ числом, большим 1
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 7 нояб. 2009 14:58 | IP
|
|
Karim
Начинающий
|
RKI, извините, не могу понять, как вы получили вероятность равную 3/4! У меня такая не получается
|
Всего сообщений: 86 | Присоединился: октябрь 2009 | Отправлено: 7 нояб. 2009 15:09 | IP
|
|
|
Форум
Решение задач по теории вероятности
