RKI 


Долгожитель
|
    
Цитата: Karim написал 5 нояб. 2009 17:49
Задача 3.
Брошены 2 игральные кости. Найти вероятность следующих событий:
а) сумма выпавших очков равна 7.
б) сумма очков равна 10, а произведение 21.
в)сумма очков расположена в промежутке (7, 9).
г) разность очков меньше 7.
решение
всего 2 кубика могут выпасть 6*6=36 способами.
а) число исходов, удовлетворяющих данному условию равно 6
p=6/36=1/6
б)число событий, удовлетворяющих данному условию 0, т.к нет таких чисел на гранях кубика, чтоб произведение было бы 21.
p=0/36=0.
в)данному промежутку удовлетворяет только чисто 8, а число событий, благоприятствующих данному событию равно 5
р=5/36.
г) т.к. максимальная разность между цифрами на двух кубиках может быть 5, то все варианты которые могут быть удовлетворяют нашему событию
р=36/36
Да, правильно
Если можно я дала бы совет: указать пространства благоприятных событий.
Например, для а) {16; 25; 34; 43; 52; 61}
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 6 нояб. 2009 8:09 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Karim написал 6 нояб. 2009 0:17
Посмотрите пожалуйста еще одну задачу.
Задача 4.
Детали изготовляются на трех станках: 30% -на первом, 50%-на втором, 20%-на третьем. Вероятность изготовления брака на каждом станке соответственно равна 0,1, 0,15, 0,005. Найти вероятность того, что извлеченная наудачу деталь бракованная.
Решение.
По формуле полной вероятности при n=3 получаем
Р(А)=Р(H1)*Р(А/H1)+Р(H2)*Р(А/H2)+Р(А)*Р(А/H3)=0,3*0,1+0,5*0,15+0,2*0,05=0,115.
Верно решена?
Верно
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 6 нояб. 2009 8:11 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Ulenka20 написал 5 нояб. 2009 22:49
Устройство состоит из 1000 элементов, работающих независимо один от другого. Вероятность отказа любого элемнта в течении времени t равна 0,002. Необходимо:
а) составить закон распределения числа отказавших за время t элементов;
б) найти математическое ожидание и дисперсию этой случайной величины;
в) определить вероятность того, что за время t откажет хотя-бы один элемент.
 - общее количество элементов. - общее количество элементов.
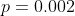 - вероятность того, что отдельно взятый элемент откажет за время t. - вероятность того, что отдельно взятый элемент откажет за время t.
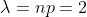
Пусть случайная величина X - число отказавших за время t элементов.
Событие {X=m} означает, что m элементов отказали за время t, а 1000-m элементов находятся в рабочем состоянии.
m = 0, 1, 2, ..., 1000
Посчитаем вероятность события {X=m}. Значение n достаточно велико, значение p достаточно мало, и np < 10. Следовательно, вместо формулы Бернулли воспользуемся ее предельной вариацией - формулой Пуассона:
 = \frac{\lambda^{m} }{m!}e^{-\lambda} = \frac{2^{m} }{m!}e^{-2} )
Таким образом, случайная величина X имеет распределение Пуассона.
Для случайных величин, имеющих распределение Пуассона, известны формулы вычисления математичесого ожидания и дисперсии:
 = \lambda = 2 )
 = \lambda = 2)
Вывод данных формул Вы можете посмотреть здесь:
http://exir.ru/cgi-bin/ikonboard/topic.cgi?forum=7&topic=2182&start=470
пример 456
 = 1 - P(m < 1) = 1 - P(m=0) = 1 - \frac{2^{0} }{0!}e^{-2} = 1 - e^{-2} )
(Сообщение отредактировал RKI 6 нояб. 2009 8:30)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 6 нояб. 2009 8:21 | IP
|
|
Natasha

Новичок
|
    
Помогите, нужно решить задачу очень срочно. Заранее благодарна за ответ.
Два стрелка стреляют по мишеням. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0.7, для второго 0.9. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
|
Всего сообщений: 25 | Присоединился: ноябрь 2008 | Отправлено: 6 нояб. 2009 9:42 | IP
|
|
Ulenka20

Новичок
|
    
Огромное спасибо, RKI!
И еще возник один вопрос с задачей:
Двумерная случайная величина (X,Y) распределена равномерно внутри квадрата R c центромв начале координат. Стороны квадрата равны корень из 2 и составляют углы 45 с осями координат.
Определить:
а) ковариацию и коэфициент корреляции случайных величин X и Y;
б) коррклированы или некоррелированы случайные величины.
Мне ишут в одном месте, что:
"Конечно, эти случайные величины коррелированы.
Например, потому, что при различных X диапазон возможных значений У различен.
В то же время, ковариация и, следовательно, коэффициент корреляции равны 0.
Дело в том, что при любых X распределение Y симметрично относительно 0, и все матожидания в выражении ковариации равны 0.
Это пример того, что для независимых величин корреляция всегда нулевая, а обратное, как видите, неверно."
А в другом, что:
"О двумерной случайной величине. Нужно вычислить математические ожидания случайных величин X, Y и XY. ДЛя этого надо вычислить интегралы по области симметричной относительно осей координат от функций: x, y и xy, умноженных на 1/2 (плотность). Все эти интегралы равны нулю. Это следует из симметрии (функций и области) и независимости интеграла от способа дробления при составлении интегральных сумм (можно выбрать так дробление, что интегральные суммы равны нулю). Ковариация равна нулю. Случайные величины некоррелированы."
Авторитетнее 2-е место, но прошу подсказать. Не могу понять как считать интеграллы, т.е. не ясно как записать плотность распр вероятносьти для этой функции и как потом "составить" интегралы... Помогите...
|
Всего сообщений: 16 | Присоединился: ноябрь 2009 | Отправлено: 6 нояб. 2009 10:13 | IP
|
|
Ulenka20

Новичок
|
    
Цитата: Natasha написал 6 нояб. 2009 9:42
Помогите, нужно решить задачу очень срочно. Заранее благодарна за ответ.
Два стрелка стреляют по мишеням. Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0.7, для второго 0.9. Найти вероятность того, что при одном залпе в мишень попадает только один из стрелков.
Попробую Вам помоч, т.к. мне тоже помогали...
Это расчитывается исходя из полной вероятности.
Вероятность того, что попадет только один стрелок - это сумма вероятностей: 1-я - попадет только первый стрелок (второй промажет)+ 2-я попадет только второй стрелок (первый промажет).
попадет только первый стрелок 0.7*(1-0.9);
попадет только второй 0.9*(1-0.7);
Таким образом вероятность того, что попадет только один стрелок: P=0.7*(1-0.9)+0.9*(1-0.7)=0.34
|
Всего сообщений: 16 | Присоединился: ноябрь 2009 | Отправлено: 6 нояб. 2009 10:24 | IP
|
|
RKI 


Долгожитель
|
    
Ulenka20
Плотность распределения двумерной случайной величины (X,Y) имеет вид:
h(x,y) = {1/2, (x,y) из R
{0, (x,y) не из R
---------------------------------------------------------------------
Найдем плотность распределения случайной величины X.
 = \int\limits_{-\infty}^{+\infty} h(x,y)dy )
Если x < - 1, то
 = \int\limits_{-\infty}^{+\infty} 0 dy = 0 )
Если x > 1, то
 = \int\limits_{-\infty}^{+\infty} 0 dy = 0 )
Если -1 <= x <= 1, то
 = \int\limits_{-\infty}^{+\infty} h(x,y)dy = )
dy + \int\limits_{|x|-1}^{1-|x|} h(x,y)dy + \int\limits_{1-|x|}^{+\infty} h(x,y)dy = )
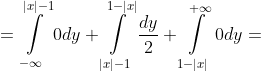
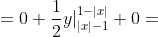
 = \frac{1}{2}(2-2|x|) = 1 - |x| )
f(x) = {0, x < - 1
{1 - |x|, -1 <= x <= 1
{0, x > 1
----------------------------------------------------------------------------
Найдем плотность распределения случайной величины Y.
 = \int\limits_{-\infty}^{+\infty} h(x,y)dx )
Если y < -1, то
 = \int\limits_{-\infty}^{+\infty} 0dx = 0 )
Если y > 1, то
 = \int\limits_{-\infty}^{+\infty} 0dx = 0 )
Если -1 <= y <= 1, то
 = \int\limits_{-\infty}^{+\infty} h(x,y)dx = )
dx + \int\limits_{|y|-1}^{1-|y|} h(x,y)dx + \int\limits_{1-|y|}^{+\infty} h(x,y)dx = )
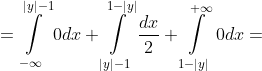
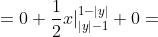
 = \frac{1}{2} (2 - 2|y|) = 1 - |y| )
g(y) = {0, y < -1
{1 - |y|, -1 <= y <= 1
{0, y > 1
Далее (в следующем сообщении) посчитаем ковариацию
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 6 нояб. 2009 10:49 | IP
|
|
Ulenka20

Новичок
|
    
RKI, я даже не знаю как Вас благодарить... Такая оперативность и качество!
|
Всего сообщений: 16 | Присоединился: ноябрь 2009 | Отправлено: 6 нояб. 2009 10:59 | IP
|
|
RKI 


Долгожитель
|
    
Ulenka20
 = \int\limits_{-\infty}^{+\infty} \int\limits_{-\infty}^{+\infty} xyh(x,y) dxdy = )
dxdy = \iint\limits_{R} \frac{xy}{2}dxdy = \frac{1}{2} \int\limits_{R} xydxdy = )
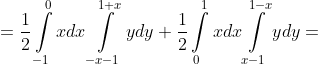
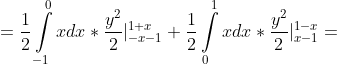
^{2} - (-x-1)^{2}) + \frac{1}{4} \int\limits_{0}^{1} xdx*((1-x)^{2} - (x-1)^{2}) = )
dx + \frac{1}{4} \int\limits_{0}^{1} x(1 - 2x + x^{2} - x^{2} + 2x - 1)dx = )
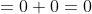
 = 0 )
-------------------------------------------------------------------------------
 = \int\limits_{-\infty}^{+\infty} xf(x)dx = \int\limits_{-\infty}^{-1} xf(x)dx + \int\limits_{-1}^{1} xf(x)dx + \int\limits_{1}^{+\infty} xf(x)dx = )
dx + \int\limits_{1}^{+\infty} 0dx = )
dx + 0 = )
dx = \int\limits_{-1}^{0} x(1 - |x|)dx + \int_{0}^{1} x(1 - |x|)dx = )
dx + \int\limits_{0}^{1} x(1-x)dx = \int\limits_{-1}^{0} (x + x^{2})dx + \int\limits_{0}^{1} (x - x^{2})dx = )
 |_{-1}^{0} + (\frac{x^{2} }{2} - \frac{x^{3} }{3}) |_{0}^{1} = )
 - (\frac{1}{2} - \frac{1}{3}) + (\frac{1}{2} - \frac{1}{3}) - (0 - 0) = )
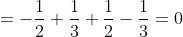
 = 0 )
Аналогично  = 0 )
 = M(XY) - M(X)M(Y) = 0 - 0 = 0 )
(Сообщение отредактировал RKI 6 нояб. 2009 11:15)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 6 нояб. 2009 11:12 | IP
|
|
RKI 


Долгожитель
|
    
Ulenka20
 = \frac{cov(X,Y)}{\sigma (X)\sigma (Y)} = 0 )
Следовательно, случайные величины некоррелированы
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 6 нояб. 2009 11:17 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности