Legalise
Новичок
|
      
Извините пожалуйста((Не получается просто скинуть то, что нужно...сейчас снова попробую)
|
Всего сообщений: 5 | Присоединился: ноябрь 2009 | Отправлено: 4 нояб. 2009 3:30 | IP
|
|
Legalise
Новичок
|
Пришлите на мыло ответ, пожалуйста)Очень срочно!!!Заранее благодарен))
1) 
2) 
|
Всего сообщений: 5 | Присоединился: ноябрь 2009 | Отправлено: 4 нояб. 2009 3:50 | IP
|
|
RKI 
Долгожитель
|
Цитата: STUDENT JURFAKA RGU написал 3 нояб. 2009 17:55
4. Отлитые болванки поступают на обработку из двух цехов: 70% из первого и 30% из второго. При этом болванки первого цеха имеют 10% брака, второго 5%. Найти вероятность того, что взятая наугад болванка:
а) не имеет дефектов и "пришла" из первого цеха (событие С);
б) не имеет дефектов (событие В)
H1 = {болванка поступила с первого цеха}
H2 = {болванка поступила со второго цеха}
P(H1) = 0.7
P(H2) = 0.3
B = {болванка не имеет дефектов}
B|H1 = {болванка не имеет дефектов при условии, что она поступила из первого цеха}
B|H2 = {болванка не имеет дефектов при условии, что она поступила из второго цеха}
P(B|H1) = 1 - 0.1 = 0.9
P(B|H2) = 1 - 0.05 = 0.95
По формуле полной вероятности
P(B) = P(H1)P(B|H1) + P(H2)P(B|H2) =
= (0.7)*(0.9) + (0.3)*(0.95) = 0.63 + 0.285 = 0.915
C = {болванка не имеет дефектов и поступила из первого цеха}
C = BH1
P(C) = P(BH1) = P(H1)P(B|H1) = (0.7)*(0.9) = 0.63
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 4 нояб. 2009 13:22 | IP
|
|
RKI
Долгожитель
|
Цитата: asselka написал 3 нояб. 2009 20:09
1) СВ Х подчинена нормальному закону с математическим ожиданием, равным 0. Вероятность попадания этой СВ в интервал (-1; 1) равна 0,5. Найти среднее квадратичное отклонение и записать нормальный закон (ответ таков - 1,47)
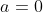
 = \Phi (\frac{1 - 0}{\sigma}) - \Phi (\frac{-1 - 0}{\sigma}) = \Phi (\frac{1}{\sigma}) - \Phi (-\frac{1}{\sigma}) = )
 + \Phi (\frac{1}{\sigma}) = 2\Phi (\frac{1}{\sigma}) = 0.5 )
 = 0.25 )
 )
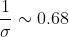
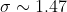
 = \frac{1}{1.47\sqrt{2\pi} }e^{-\frac{x^{2} }{4.3218} } )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 4 нояб. 2009 13:32 | IP
|
|
RKI
Долгожитель
|
Цитата: asselka написал 3 нояб. 2009 20:09
2) Вероятность появления некоторого события в одном опыте равна 0,6. Какова вероятность того, что это событие появится в большинстве из 60 опытов? (по закону больших чисел. Ответ - 0,966)
n = 60
p = 0.6
q = 1 - p = 1 - 0.6 = 0.4
np = 60*(0.6) = 36
npq = 60*(0.6)*(0.4) = 14.4
 = \Phi (\frac{60 - 36}{\sqrt{14.4} }) - \Phi (\frac{31 - 36}{\sqrt{14.4} } ) \sim )
 - \Phi (-1.32) = \Phi (6.32) + \Phi (1.32) = 0.5 + 0.4066 = 0.9066 )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 4 нояб. 2009 13:59 | IP
|
|
Vaneus
Новичок
|
ПОМОГИТЕ ПОЖАЛУЙСТА с задачами...
1. На карточках лото написаны числа от 1 до 10. Найти вероятность того, что на трёх случайно вытянутых карточках окажутся числа меньше 6.
2. Вероятность того, что необходимый материал есть на первой базе - 0.9, на второй - 0.8, на третьей - 0.6. Найти вероятность того, что этот материал есть ровно на двух базах.
3.Радиолампа может принадлежатьк одной из четырёх партий с вероятностями р1=0.2, р2=0.4, р3=0.3, р4=0,1. Вероятность того, что лампа проработает заданное время, для этих партий равна соответственно 0.5, 0.7, 0.6, 0.8. Найти вероятность того, что случайно выбранная лампа проработает заданное время.
4.В двух коробках находиться по 20 деталей, из них стандартных в первой 18, а во второй - 10. Из первой коробки взяли деталь и переложили во вторую. После этого случайно выбранная деталь со второй коробки оказалась стандартной. Какая вероятносто того, что переложили нестандартную деталь?
5. Два спортсмена независимо делают по одному выстрелу, каждый в свою мишень. Вероятность попадания в мишень для первого спортсмена - 0.6, для второго - 0.7. Рассматриваються случайные величины Х1 - число попаданий первого спортсмена, Х2 - число попаданий для второго и их разница Z=x1-x2. Построить закон распределения случайной величны Z и найти её математическое ожидание, дисперсию и среднее квадратическое отклонение.
|
Всего сообщений: 3 | Присоединился: октябрь 2009 | Отправлено: 4 нояб. 2009 14:56 | IP
|
|
RKI
Долгожитель
|
Цитата: Vaneus написал 4 нояб. 2009 14:56
1. На карточках лото написаны числа от 1 до 10. Найти вероятность того, что на трёх случайно вытянутых карточках окажутся числа меньше 6.
A = {на трех карточках числа меньше 6}
Посчитаем число n всевозможных исходов. Способов выбрать 3 числа из 10 имеющихся:
n = C(3;10) = 10!/3!7! = 120.
Посчитаем число m исходов, благоприятных событию A. Способов выбрать 3 числа из 5 подходящих (1, 2, 3, 4, 5):
m = C(3;5) = 5!/3!2! = 10.
По классическому определению вероятности
P(A) = m/n = 10/120 = 1/12
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 4 нояб. 2009 15:02 | IP
|
|
RKI
Долгожитель
|
Цитата: Vaneus написал 4 нояб. 2009 14:56
2. Вероятность того, что необходимый материал есть на первой базе - 0.9, на второй - 0.8, на третьей - 0.6. Найти вероятность того, что этот материал есть ровно на двух базах.
Ai = {материал есть на i-той базе}, i=1,2,3
P(A1) = 0.9
P(A2) = 0.8
P(A3) = 0.6
не Ai = {материала нет на i-той базе}, i=1,2,3
P(не A1) = 1 - P(A1) = 1 - 0.9 = 0.1
P(не A2) = 1 - P(A2) = 1 - 0.8 = 0.2
P(не A3) = 1 - P(A3) = 1 - 0.6 = 0.4
A = {материал есть ровно на двух базах}
A = A1*A2*(не A3) + A1*(не A2)*A3 + (не A1)*A2*A3
P(A) =
= P(A1*A2*(не A3) + A1*(не A2)*A3 + (не A1)*A2*A3) =
= P(A1*A2*(не A3)) + P(A1*(не A2)*A3) + P((не A1)*A2*A3) =
= P(A1)P(A2)P(не A3) + P(A1)P(не A2)P(A3) + P(не A1)P(A2)P(A3) =
= (0.9)*(0.8)*(0.4) + (0.9)*(0.2)*(0.6) + (0.1)*(0.8)*(0.6) =
= 0.288 + 0.108 + 0.048 = 0.444
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 4 нояб. 2009 15:10 | IP
|
|
RKI
Долгожитель
|
Цитата: Vaneus написал 4 нояб. 2009 14:56
3.Радиолампа может принадлежатьк одной из четырёх партий с вероятностями р1=0.2, р2=0.4, р3=0.3, р4=0,1. Вероятность того, что лампа проработает заданное время, для этих партий равна соответственно 0.5, 0.7, 0.6, 0.8. Найти вероятность того, что случайно выбранная лампа проработает заданное время.
Hi = {лампа из i-той партии}, i=1,2,3,4
P(H1) = 0.2
P(H2) = 0.4
P(H3) = 0.3
P(H4) = 0.1
A = {случайно выбранная лампа проработает заданное время}
A|Hi = {выбранная лампа проработает заданное время при условии, что она из i-той партии}, i=1,2,3,4
P(A|H1) = 0.5
P(A|H2) = 0.7
P(A|H3) = 0.6
P(A|H4) = 0.8
По формуле полной вероятности
P(A) =
= P(H1)P(A|H1) + P(H2)P(A|H2) + P(H3)P(A|H3) + P(H4)P(A|H4) =
= (0.2)*(0.5) + (0.4)*(0.7) + (0.3)*(0.6) + (0.1)*(0.8) =
= 0.1 + 0.28 + 0.18 + 0.08 = 0.64
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 4 нояб. 2009 15:16 | IP
|
|
RKI
Долгожитель
|
Цитата: Vaneus написал 4 нояб. 2009 14:56
4.В двух коробках находиться по 20 деталей, из них стандартных в первой 18, а во второй - 10. Из первой коробки взяли деталь и переложили во вторую. После этого случайно выбранная деталь со второй коробки оказалась стандартной. Какая вероятносто того, что переложили нестандартную деталь?
H1 = {из первой коробки во вторую переложили стандартную деталь}
H2 = {из первой коробки во вторую переложили нестандартную деталь}
P(H1) = 18/20 = 9/10
P(H2) = 2/20 = 1/10
A = {из второй коробки достали стандартную деталь}
A|H1 = {из второй коробки достали стандартную деталь, если из первой коробки во вторую переложили стандартную деталь} = {из второй коробки достали стандартную деталь, если во второй коробке 11 стандартных и 10 нестандартных деталей}
P(A|H1) = 11/21
A|H2 = {из второй коробки достали стандартную деталь, если из первой коробки во вторую переложили нестандартную деталь} = {из второй коробки достали стандартную деталь, если во второй коробке 10 стандартных и 11 нестандартных деталей}
P(A|H2) = 10/21
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) =
= (9/10)*(11/21) + (1/10)*(10/21) =
= 99/210 + 10/210 = 109/210
По формуле Байеса
P(H2|A) = P(H2)P(A|H2)/P(A) = (1/10)*(10/21)/(109/210) =
= (10/210)/(109/210) = 10/109
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 4 нояб. 2009 15:25 | IP
|
|
|
Форум
Решение задач по теории вероятности
