Skamarox
Новичок
|
    
помогите пожалуйста?!?!?!)
1) бросается три игральные кости.Являются ли события А и В независимыми, если
А=(на одной из костей выпало "1")
В=(на всех выпали разные грани)
2) из партии в пять деталей наугад взято одно изделие,оказавшееся бракованным.Какое предположение о количестве бракованных деталей наиболее вероятно, если сначала любое число бракованных изделий равновозможно.
заранее большое спасибо)
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 19:47 | IP
|
|
taaraass
Новичок
|
Большое Спасибо вам уважаемая RKI за прозрение))))
|
Всего сообщений: 6 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 19:48 | IP
|
|
RKI 
Долгожитель
|
Цитата: Slanderous написал 26 окт. 2009 19:44
RKI если возможно ответьте на вопрос - от куда в самом начале (где х>0) взялась такая вещь "(k^3)\2"
У Вас было задание найти коэффициент a
Он был и найден, и он равен (k^3)/2
Смотрите внимательно (я расписала Вашу задачу в двух сообщениях)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 19:52 | IP
|
|
Vorona
Новичок
|
 
В ящике находится 10 деталей, из которых 6 стандартных. Для производственных нужд было отобрано 2 детали случайным образом. Какова вероятность того, что следующая наугад взятая деталь окажется стандартной?
|
Всего сообщений: 7 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 20:01 | IP
|
|
RKI
Долгожитель
|
Цитата: Vorona написал 26 окт. 2009 20:01
В ящике находится 10 деталей, из которых 6 стандартных. Для производственных нужд было отобрано 2 детали случайным образом. Какова вероятность того, что следующая наугад взятая деталь окажется стандартной?
H1 = {были отобраны 2 стандартных детали}
H2 = {были отобраны 1 стандартная и 1 дефектная детали}
H3 = {были отобраны 2 дефектные детали}
P(H1) = C(2;6)/C(2;10) = 15/45 = 1/3
P(H2) = C(1;6)C(1;4)/C(2;10) = (6*4)/45 = 24/45 = 8/15
P(H3) = C(2;4)/C(2;10) = 6/45 = 2/15
A = {следующая деталь стандартная}
A|H1 = {следующая деталь стандартная, если остались 4 стандартных и 4 дефектных деталей}
A|H2 = {следующая деталь стандартная, если остались 5 стандартных и 3 дефектных деталей}
A|H3 = {следующая деталь стандартная, если остались 6 стандартных и 2 дефектных деталей}
P(A|H1) = 4/8
P(A|H2) = 5/8
P(A|H3) = 6/8
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) + P(H3)P(A|H3) =
= (5/15)*(4/8) + (8/15)*(5/8) + (2/15)*(6/8) =
= 20/120 + 40/120 + 12/120 = 72/120 = 0.6
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 20:09 | IP
|
|
Irochkacat
Новичок
|
добрый день! вот какая она должна быть)))
спасибо за первую))
Случайная величина распределена по нормальному закону с математическим ожиданием m=-3. Р{Х>3}=0,15. найти ее дисперсию,вычислить вероятность отрицательных значений случайной величины.
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 20:12 | IP
|
|
bvvmega
Новичок
|
h
|
Всего сообщений: 12 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 20:21 | IP
|
|
RKI
Долгожитель
|
Цитата: Skamarox написал 26 окт. 2009 19:47
2) из партии в пять деталей наугад взято одно изделие,оказавшееся бракованным.Какое предположение о количестве бракованных деталей наиболее вероятно, если сначала любое число бракованных изделий равновозможно.
H0 = {5 стандартных деталей}
H1 = {4 стандартных и 1 дефектное деталей}
H2 = {3 стандартных и 2 дефектных деталей}
H3 = {2 стандартных и 3 дефектных деталей}
H4 = {1 стандартная и 4 дефектных деталей}
H5 = {5 дефектных деталей}
P(H0) = P(H1) = P(H2) = P(H3) = P(H4) = P(H5) = 1/6
A = {достали бракованное изделие}
P(A|H0) = 0
P(A|H1) = 1/5
P(A|H2) = 2/5
P(A|H3) = 3/5
P(A|H4) = 4/5
P(A|H5) = 1
По формуле полной вероятности
P(A) = P(H0)P(A|H0) + ... + P(H5)P(A|H5) =
= (1/6)(0 + 1/5 + 2/5 + 3/5 + 4/5 + 1) = 3/6 = 1/2
По формуле Байеса
P(H0|A) = P(H0)P(A|H0)/P(A) = 0
P(H1|A) = P(H1)P(A|H1)/P(A) = (1/30)/(1/2) = 1/15
P(H2|A) = P(H2)P(A|H2)/P(A) = (2/30)/(1/2) = 4/30 = 2/15
P(H3|A) = P(H3)P(A|H3)/P(A) = (3/30)/(1/2) = 3/15 = 1/5
P(H4|A) = P(H4)P(A|H4)/P(A) = (4/30)/(1/2) = 8/30 = 4/15
P(H5|A) = P(H4)P(A|H4)/P(A) = (1/6)/(1/2) = 2/6 = 1/3
Ответ.
{5 стандартных деталей} - 0%
{4 стандартных и 1 дефектное деталей} - 6,67%
{3 стандартных и 2 дефектных деталей} - 13,33%
{2 стандартных и 3 дефектных деталей} - 20%
{1 стандартная и 4 дефектных деталей} - 26,67%
{5 дефектных деталей} - 33,33%
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 20:23 | IP
|
|
RKI
Долгожитель
|
Цитата: Irochkacat написал 26 окт. 2009 20:12
Случайная величина распределена по нормальному закону с математическим ожиданием m=-3. Р{Х>3}=0,15. найти ее дисперсию,вычислить вероятность отрицательных значений случайной величины.
 = 0.5 - \Phi (\frac{3-m}{\sigma}) = 0.5 - \Phi (\frac{6}{\sigma}) = 0.15 )
 = 0.35 )
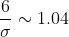
 = \sigma^{2} \sim 33.2929 )
 = 0.5 + \Phi (\frac{0+3}{5.77}) \sim 0.5 + \Phi (0.52) \sim 0.5 + 0.1985 = 0.6985 )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 20:41 | IP
|
|
faizer
Новичок
|
помогите пожалуйста!
Задача 1.Изготовлена партия из 200 изделий,в которой оказались 3 бракованные.Произведена выборка из 5 изделий.Найти вероятность того,что в выборке не будет ни одного бракованного изделия.
Задача 2.На автозавод поступили двигатели от трех моторных заводов. От первого завода поступило 10 двигателей, от второго 6, а от третьего 4. Вероятность безотказной работы этих двигателей в течение гарантийного срока соответственно равны: 0,9; 0,8; 0,7. Какова вероятность того, что проработавший без дефекта двигатель изготовлен на первом заводе?
(Сообщение отредактировал faizer 27 окт. 2009 0:23)
|
Всего сообщений: 5 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 20:45 | IP
|
|
Форум
Решение задач по теории вероятности
