Elenkaaa
Новичок
|
    
помогите пожалуйста у меня экзамен,определить вероятность попадания при одном выстреле,если с вероятностью,равной 0,8, при четырех выстрелах было 2 попадания
|
Всего сообщений: 5 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 17:05 | IP
|
|
RKI 
Долгожитель
|
Цитата: Slanderous написал 26 окт. 2009 15:43
Плотность вероятности случайной величины Х равна
f(x) = a*(x)^2 * e^-kx. k>0. 0<=x<+бесконечности.
Найти коэффициент "а", F(x), P(0<x<1\k)
Заранее спасибо
 = \int\limits_{-\infty}^{x} f(t)dt )
Если x <= 0, то
 = \int\limits_{-\infty}^{x} f(t)dt = \int\limits_{-\infty}^{x} 0dt = 0 )
Если x > 0, то
 = \int\limits_{-\infty}^{x} f(t)dt = \int\limits_{-\infty}^{0} f(t)dt + \int\limits_{0}^{x} f(t)dt = )
 = )
 = )
 = )
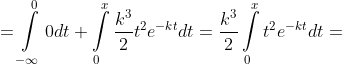
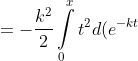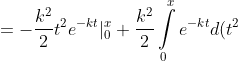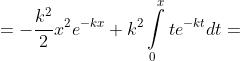
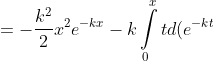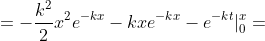
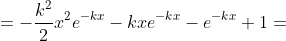
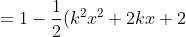e^{-kx} )
F(x) = {1 - (1/2)((k^2)(x^2) + 2kx + 2)(e^(-kx)), x > 0
{0, x <= 0
 = F(\frac{1}{k}) - F(0) = )
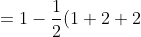e^{-1} - 0 = 1 - \frac{5}{2}e^{-1} )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 17:18 | IP
|
|
taaraass
Новичок
|
Большое спасибо вам RKI за решение задач. Вы просто супер.
Я очень вам благодарен!!!!!
(Сообщение отредактировал taaraass 26 окт. 2009 17:45)
|
Всего сообщений: 6 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 17:44 | IP
|
|
taaraass
Новичок
|
уважемый(я) не могли бы вы просто проверить правильности решения задачи.
Вероятность попадания в мишень для 1, 2, 3 спортсмена равна 0,9; 0,6; 0,8. Каждый спортсмен делает 1 выстрел. Найти вероятность того, что в мишени будет ровно 1 пробоина?
Решение:
А1={1 спортсмен попал в мишень}
А2={2 спортсмен попал в мишень}
А3={3 спортсмен попал в мишень}
Р(А1)=0,9
Р(А2)=0,6
Р(А3)=08
В=в мишени только 1 пробоина
Р(В)=Р(А1)*Р(А\Н1)+Р(А2)*Р(А\Н2)+Р(А3)*Р(А\Н3)
Р(А\Н1)=1-0,9=0,1
Р(А\Н1)=1-0,6=0,4
Р(А\Н1)=1-0,8=0,2
Р(В)=0,9*0,1+0,4*0,6+0,2*0,8=0,49
|
Всего сообщений: 6 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 18:58 | IP
|
|
Sun Summer
Новичок
|
Цитата: RKI написал 26 окт. 2009 9:38
Цитата: Sun Summer написал 26 окт. 2009 5:27
Задача: Случайная величина X распределена нормально с математическим ожиданием а= 10 и средним квадратическим отклонением 
. Найти интервал, в который с вероятностью 0,9973 попадет X в результате испытания.
Решение: Вероятность того, что абсолютная величина отклонения меньше положительного числа  , вычисляется по формуле 
. В нашем случае  , откуда  по таблице значений функции  получаем, что  , 
, то есть 
Значит интервал имеет вид 
Задачка сложноватая. Скажите, правильно ли она решена? и если да, то объясните, пожалуйста, откуда взялась эта формула ? Лапласа по другому выглядит, эту же нигде не нашёл, кучу учебников перерыл
Задача решена правильно.
Пусть случайная величина X распределена нормально с параметрами a (математическое ожидание) и 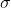 (среднее квадратическое отклонение).
Известно, что функция распределения случайной величины X имеет вид:
 = P(X<x) = 0.5 + \Phi (\frac{x-a}{\sigma}) )
Тогда
 = F(x_{2}) - F(x_{1}) = \Phi (\frac{x_{2}-a}{\sigma}) - \Phi (\frac{x_{1}-a}{\sigma}) )
Также известно, что функция Лапласа является нечетной, то есть
 = -\Phi (x) )
Следовательно,
 = P(-\delta < X-a < \delta) = P(a-\delta < X < a+\delta) = )
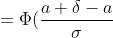 - \Phi (\frac{a-\delta - a}{\sigma}) = \Phi (\frac{\delta}{\sigma}) - \Phi (-\frac{\delta}{\sigma}) = )
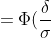 + \Phi (\frac{\delta}{\sigma}) = 2\Phi (\frac{\delta}{\sigma}) )
RKI, спасибо! А скажите, пожалуйста, мне вывод этой формулы нужно расписывать в решении задачи? или же можно использовать как готовую, типа препод поймёт но с другой стороны нигде её не видел
|
Всего сообщений: 16 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 19:03 | IP
|
|
taaraass
Новичок
|
Подскажите пожалуйста. В решении задачи
В ящике есть 10 шаров з номерами 1,2,3,4,5,6,7,8,9,10. Наудачу вынимают5 шаров. Какая вероятность того что среди вытянутых шаров найдут шары з номерами 7 и 8.
Мы Посчитаем число m исходов, благоприятных событию A.
Способов вытащить 7 из имеющейся одной семерки: m1 = 1.
Способов вытащить 8 из имеющейся одной восьмерки: m2 = 1.
Способов вытащить еще 3 цифры из 8 оставшихся:
m3 = C(3;8) = 8!/3!5! = 56.
так вот почему мы берём 3 цифры из 8 оставшихся, а например не 2, 4 или 5)))
Подскажите, а то я что то не понял.
ДА ИЗВИИТЕ ЗА БЕСПОКОЙСТВО, ЗАРАНИЕ СПАСИБО.
|
Всего сообщений: 6 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 19:04 | IP
|
|
RKI
Долгожитель
|
Цитата: taaraass написал 26 окт. 2009 18:58
Вероятность попадания в мишень для 1, 2, 3 спортсмена равна 0,9; 0,6; 0,8. Каждый спортсмен делает 1 выстрел. Найти вероятность того, что в мишени будет ровно 1 пробоина?
Ai = {i-тый стрелок попал в мишень}, i=1,2,3
P(A1) = 0.9
P(A2) = 0.6
P(A3) = 0.8
не Ai = {i-тый стрелок промахнется}, i=1,2,3
P(не A1) = 1 - P(A1) = 1 - 0.9 = 0.1
P(не A2) = 1 - P(A2) = 1 - 0.6 = 0.4
P(не A3) = 1 - P(A3) = 1 - 0.8 = 0.2
A = {только одна пробоина}
A = A1*(не A2)*(не A3) + (не A1)*A2*(не A3) + (не A1)*(не A2)*A3
P(A) =
= P(A1*(не A2)*(не A3) + (не A1)*A2*(не A3) + (не A1)*(не A2)*A3) =
= P(A1*(не A2)*(не A3)) + P((не A1)*A2*(не A3)) + P((не A1)*(не A2)*A3)) =
= P(A1)*P(не A2)*P(не A3) + P(не A1)*P(A2)*P(не A3) + P(не A1)*P(не A2)*P(A3) =
= (0.9)*(0.4)*(0.2) + (0.1)*(0.6)*(0.2) + (0.1)*(0.4)*(0.8) =
= 0.072 + 0.012 + 0.032 = 0.116
P.S. Я - это она
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 19:06 | IP
|
|
RKI
Долгожитель
|
Цитата: Sun Summer написал 26 окт. 2009 19:03
RKI, спасибо! А скажите, пожалуйста, мне вывод этой формулы нужно расписывать в решении задачи? или же можно использовать как готовую, типа препод поймёт но с другой стороны нигде её не видел
Я думаю, вывод данной формулы расписывать ни к чему.
Это очень известные в теории вероятностей формулы, тем более для преподавателя.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 19:08 | IP
|
|
RKI
Долгожитель
|
Цитата: taaraass написал 26 окт. 2009 19:04
Мы Посчитаем число m исходов, благоприятных событию A.
Способов вытащить 7 из имеющейся одной семерки: m1 = 1.
Способов вытащить 8 из имеющейся одной восьмерки: m2 = 1.
Способов вытащить еще 3 цифры из 8 оставшихся:
m3 = C(3;8) = 8!/3!5! = 56.
так вот почему мы берём 3 цифры из 8 оставшихся, а например не 2, 4 или 5)))
Подскажите, а то я что то не понял.
Всего выбирается 5 цифр из 10 имеющихся: 1, 2, 3, ..., 10.
Цифры 7 и 8 мы выбрали.
Значит, осталось выбрать еще 5-2 = 3 цифры из имеющихся: 1, 2, 3, 4, 5, 6, 9, 10.
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 19:10 | IP
|
|
Slanderous
Новичок
|
RKI если возможно ответьте на вопрос - от куда в самом начале (где х>0) взялась такая вещь "(k^3)\2"
|
Всего сообщений: 9 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 19:44 | IP
|
|
|
Форум
Решение задач по теории вероятности
