Elenkaaa
Новичок
|
    
в мастерской имеется 20 моторов. Вероятность того, что мотор работает с полной нагрузкой , равна 0,9. Найти вероятность того , что 15 моторов работает с полной нагрузкой.Заранее спс.
(Сообщение отредактировал Elenkaaa 26 окт. 2009 12:20)
|
Всего сообщений: 5 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 10:59 | IP
|
|
RKI 
Долгожитель
|
Цитата: Elenkaaa написал 26 окт. 2009 10:59
в мастерской имеется 20 моторов. Вероятность того, что мотор работает с полной нагрузкой , равна 0,9. Найти вероятность того , что 15 моторов работает с полной нагрузкой.Заранее спс.
n = 20 - количество моторов
p = 0.9 - вероятность того, что мотор работает с полной нагрузкой
q = 1 - p = 1 - 0.9 = 0.1
m - количество моторов, работающих с полной нагрузкой
P(m=15) = C(15;20)*((0.9)^15)*((0.1)^5) =
= 15504*(0.205891132094649)*(0.00001) =
= 0.03192136111995438096
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 15:18 | IP
|
|
RKI
Долгожитель
|
Цитата: taaraass написал 25 окт. 2009 20:33
№1 В 1 коробке есть 7 белых и 5 черных шаров. В 2й есть 1 белый и 6 черных. З 1й во 2 переложили наудачу 1 шар. После чего з 2й коробки наудачу вытащили 1 шар, которая оказалась черной. Найти вероятность того что было переложено белый шар.
H1 = {из первой коробки во вторую переложили белый шар}
H2 = {из первой коробки во вторую переложили черный шар}
P(H1) = 7/(7+5) = 7/12
P(H2) = 5/(7+5) = 5/12
A = {из второй коробки достали черный шар}
A|H1 = {из второй коробки достали черный шар, если в ней 2 белых и 6 черных шаров}
A|H2 = {из второй коробки достали черный шар, если в ней 1 белый и 7 черных шаров}
P(A|H1) = 6/8
P(A|H2) = 7/8
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) =
= (7/12)*(6/8) + (5/12)*(7/8) = 42/96 + 35/96 = 77/96
По формуле Байеса
P(H1|A) = P(H1)P(A|H1)/P(A) = (7/12)(6/8)/(77/96) =
= (42/96)/(77/96) = 42/77 = 6/11
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 15:25 | IP
|
|
blendas
Новичок
|
Здравствуйте, помогите пожалуйста!
Задача 1. На пункте отправления имеются 20 заказов на отправку товара - 5 в США, 10 - во Францию, 5 - внутри страны. Какова вероятность, что выбранные наугад 2 товара окажутся предназначены - один для отправки внутри страны, другой - на экспорт.
Задача 2. Компания состоящая из 12 мужчин и 15 женщин случ.образом разбилась на 3 группы по 9 человек. Найти вер-ть того, что в каждой группе будет по 4 мужчины.
Решение:
n= С(9,27) = 27!/9!18! = 4 686 825
m= С(4,12)*С(5,15)*3!=495*3003*6= 8 918 910 (вот здесь, скорее всего, ошибка, помогите в расчете)
P(А)= m/n
|
Всего сообщений: 10 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 15:30 | IP
|
|
Slanderous
Новичок
|
Здравствуйте, помогите пожалуйста с задачей. До завтра нужно решение
Плотность вероятности случайной величины Х равна
f(x) = a*(x)^2 * e^-kx. k>0. 0<=x<+бесконечности.
Найти коэффициент "а", F(x), P(0<x<1\k)
Заранее спасибо
|
Всего сообщений: 9 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 15:43 | IP
|
|
RKI
Долгожитель
|
Цитата: taaraass написал 25 окт. 2009 21:21
Случайная величина Х имеет функцию распределения F(x). Найти вероятность попадания в интервал (А;B) цельность распределения; математическое ожидание, диспресию и среднее квадратичное отклонение. Построить графики функций распределения и плотности распределения.
{0 при x<=0
F(x) { (х*х+х)\2 при 0<x<=1
{1 при x>1
а=0,2; в=1
F(x) = {0, x <= 0
{(x^2 + x)/2, 0 < x <= 1
{1, x > 1
P(0.2 < X < 1) = F(1) - F(0.2) = (1+1)/2 - (0.04+0.2)/2 =
= 1 - 0.12 = 0.88
f(x) = F'(x)
f(x) = {0, x < 0
{(2x+1)/2, 0 < x < 1
{0, x > 1
 = \int\limits_{-\infty}^{+\infty} xf(x)dx = \int\limits_{-\infty}^{0} xf(x)dx + \int\limits_{0}^{1} xf(x)dx + \int\limits_{1}^{+\infty} xf(x)dx = )
dx + \int\limits_{1}^{+\infty} 0dx = 0 + (\frac{x^{3} }{3} + \frac{x^{2} }{4}) |_{0}^{1} + 0 = )
 = \frac{7}{12} )
 = \int\limits_{-\infty}^{+\infty} x^{2} f(x)dx = \int\limits_{-\infty}^{0} x^{2} f(x)dx + \int\limits_{0}^{1} x^{2} f(x)dx + \int\limits_{1}^{+\infty} x^{2} f(x)dx = )
dx + \int\limits_{1}^{+\infty} 0dx = 0 + (\frac{x^{4} }{4} + \frac{x^{3} }{6}) |_{0}^{1} + 0 = )
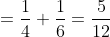
 = \frac{5}{12} )
 = M(X^{2}) - M^{2} (X) = \frac{5}{12} - \frac{49}{144} = \frac{11}{144} )
} = \sqrt{\frac{11}{144} } = \frac{\sqrt{11} }{12} )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 15:51 | IP
|
|
RKI
Долгожитель
|
Цитата: taaraass написал 25 окт. 2009 20:33
№2 в ящике есть 10 шаров з номерами 1,2,3,4,5,6,7,8,9,10. Наудачу вынимают5 шаров. Какая вероятность того что среди вытянутых шаров найдут шары з номерами 7 и 8.
A = {среди вытянутых 5 шаров есть шары с номерами 7 и 8}
Посчитаем число n всевозможных исходов.
Способов вытащить 5 шаров из 10 имеющихся:
n = C(5;10) = 10!/5!5! = 252.
Посчитаем число m исходов, благоприятных событию A.
Способов вытащить 7 из имеющейся одной семерки: m1 = 1.
Способов вытащить 8 из имеющейся одной восьмерки: m2 = 1.
Способов вытащить еще 3 цифры из 8 оставшихся:
m3 = C(3;8) = 8!/3!5! = 56.
По правилу произведения m = m1*m2*m3 = 1*1*56 = 56.
По классическому определению вероятности
P(A) = m/n = 56/252 = 2/9
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 15:57 | IP
|
|
RKI
Долгожитель
|
Цитата: Petite Fille написал 25 окт. 2009 23:04
В первой урне находятся 6 шаров белого и 2 шара черного цвета, во второй - 6 белого и 4 синего, в третьей - 5 белого и 5 красного цвета. Из первой и второй урны наудачу извлекают по одному шару и кладут в третью. После этого из третьей вынимают один шар. Найти вероятность того, что он окажется белым.
H1 = {из первой и второй урны достали по белому шару}
H2 = {из первой урны достали белый шар, а из второй - синий}
H3 = {из первой урны достали черный шар, а из второй - белый}
H4 = {из первой урны достали черный шар, а из второй - синий}
P(H1) = (6/8)*(6/10) = 36/80 = 9/20
P(H2) = (6/8)*(4/10) = 24/80 = 6/20
P(H3) = (2/8)*(6/10) = 12/80 = 3/20
P(H4) = (2/8)*(4/10) = 8/80 = 2/20
A = {из третьей урны достали белый шар}
A|H1 = {из третьей урны достали белый шар, если в ней 7 белых и 5 черных шаров}
A|H2 = {из третьей урны достали белый шар, если в ней 6 белых, 5 красных и 1 синий шар}
A|H3 = {из третьей урны достали белый шар, если в ней 1 черный, 6 белых и 5 красных шаров}
A|H4 = {из третьей урны достали белый шар, если в ней 5 белых, 5 красных, 1 синий и 1 черный шары}
P(A|H1) = 7/12
P(A|H2) = 6/12
P(A|H3) = 6/12
P(A|H4) = 5/12
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) + P(H3)P(A|H3) + P(H4)P(A|H4) =
= (9/20)*(7/12) + (6/20)*(6/12) + (3/20)*(6/12) + (2/20)*(5/12) =
= 63/240 + 36/240 + 18/240 + 10/240 = 127/240
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 16:11 | IP
|
|
RKI
Долгожитель
|
Цитата: blendas написал 26 окт. 2009 15:30
Задача 1. На пункте отправления имеются 20 заказов на отправку товара - 5 в США, 10 - во Францию, 5 - внутри страны. Какова вероятность, что выбранные наугад 2 товара окажутся предназначены - один для отправки внутри страны, другой - на экспорт.
A = {один товар - внутри страны, второй товар - на экспорт}
Посчитаем число n всевозможных исходов. Способов выбрать 2 товара из 20 имеющихся:
n = C(2;20) = 20!/2!18! = 190.
Посчитаем число m исходов, благоприятных событию A.
Способов выбрать 1 товар для отправки внутри страны из 5 имеющихся:
m1 = C(1;5) = 5!/1!4! = 5.
Способов выбрать 1 товар для экспорта из 15 имеющихся:
m2 = C(1;15) = 15!/1!14! = 15.
По правилу произведения m = m1*m2 = 5*15 = 75.
По классическому определению вероятности
P(A) = m/n = 75/190 = 15/38
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 16:19 | IP
|
|
RKI
Долгожитель
|
Цитата: Slanderous написал 26 окт. 2009 15:43
Плотность вероятности случайной величины Х равна
f(x) = a*(x)^2 * e^-kx. k>0. 0<=x<+бесконечности.
Найти коэффициент "а", F(x), P(0<x<1\k)
f(x) = {a(x^2)(e^(-kx)), x >= 0
{0, x < 0
dx = 1 )
dx = \int\limits_{-\infty}^{0} f(x)dx + \int\limits_{0}^{+\infty} f(x)dx = )
 = )
 = )
 = )
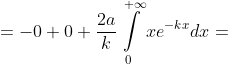
f(x) = {(k^3)(x^2)(e^(-kx))/2, x >= 0
{0, x < 0
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 17:01 | IP
|
|
|
Форум
Решение задач по теории вероятности
