asselka
Новичок
|
    
Спасибо вам огромное!!!!!!!!!!!!!!!!!!!
|
Всего сообщений: 16 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 17:55 | IP
|
|
Kuziaa
Новичок
|
Здравствуйте, помогите пожалуйста, задача сложная и как её решить незнаю, а сдать надо =((( Помогите пожалуйста с решением.
Случайные величины X и Y заданы законами распределений. Определить математическое ожидание, дисперсию и среднее квадратическое отклонение случайных величин X и Y. Составить законы распределения случайных величин Z=X+Y, V=XY. Построить многоугольник распределения вероятностей случайной величины Z. Найти математическое ожидание и дисперсию случайной величины W=2X-4Y.
|
Всего сообщений: 5 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 19:08 | IP
|
|
|
|
Kuziaa
Новичок
|
Ой, RKI, простите меня пожалуйста за то, что поиском не воспользовался. Спасибо вам большое за помощь.
|
Всего сообщений: 5 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 20:07 | IP
|
|
taaraass
Новичок
|
Здравствуйте. Извините если отвлекаю. Но помогите пожалуйста решить 2 задачки. завтра надо сдать. зарание спасибо.
№1 В 1 коробке есть 7 белых и 5 черных шаров. В 2й есть 1 белый и 6 черных. З 1й во 2 переложили наудачу 1 шар. После чего з 2й коробки наудачу вытащили 1 шар, которая оказалась черной. Найти вероятность того что было переложено белый шар.
№2 в ящике есть 10 шаров з номерами 1,2,3,4,5,6,7,8,9,10. Наудачу вынимают5 шаров. Какая вероятность того что среди вытянутых шаров найдут шары з номерами 7 и 8.
|
Всего сообщений: 6 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 20:33 | IP
|
|
taaraass
Новичок
|
да и еще 1. Думал решщить сам да что то не выходит(((.
Случайная величина Х имеет функцию распределения F(x). Найти вероятность попадания в интервал (А;B) цельность распределения; математическое ожидание, диспресию и среднее квадратичное отклонение. Построить графики функций распределения и плотности распределения.
{0 при x<=0
F(x) { (х*х+х)\2 при 0<x<=1
{1 при x>1
а=0,2; в=1
|
Всего сообщений: 6 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 21:21 | IP
|
|
Sun Summer
Новичок
|
Цитата: RKI написал 25 окт. 2009 10:42
У нас имеется 8 предметов. Сначала выбираем из них 4 предмета (которые мы положим в первый ящик). Способов выбрать 4 предмета из 8 имеющихся:
m0 = C(4;8) = 8!/4!4! = 70.
Предположим, что мы выбрали эти четыре предмета. Рассматриваем пока именно их. Первый предмет имеет только m1=1 альтернативу, потому что он направляется в первый ящик. Аналогично для второго, третьего и четвертого предметов: m2 = m3 = m4 = 1.
Остались еще четыре нетронутых предмета. Пятый предмет имеет m5 = 2 альтернативы - либо он будеит положен во второй ящик, либо - в третий ящик. Аналогично для шестого, седьмого и восьмого предметов: m6 = m7 = m8 = 2.
По правилу произведения
m = m0*m1*...*m8 = 70*1*1*1*1*2*2*2*2 = 70*(2^4)
RKI, спасибо вам большое!
(Сообщение отредактировал Sun Summer 25 окт. 2009 21:42)
|
Всего сообщений: 16 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 21:42 | IP
|
|
Petite Fille
Новичок
|
Помогите, пожалуйста!
В первой урне находятся 6 шаров белого и 2 шара черного цвета, во второй - 6 белого и 4 синего, в третьей - 5 белого и 5 красного цвета. Из первой и второй урны наудачу извлекают по одному шару и кладут в третью. После этого из третьей вынимают один шар. Найти вероятность того, что он окажется белым.
|
Всего сообщений: 1 | Присоединился: октябрь 2009 | Отправлено: 25 окт. 2009 23:04 | IP
|
|
Sun Summer
Новичок
|
Задача: Случайная величина X распределена нормально с математическим ожиданием а= 10 и средним квадратическим отклонением 
. Найти интервал, в который с вероятностью 0,9973 попадет X в результате испытания.
Решение: Вероятность того, что абсолютная величина отклонения меньше положительного числа  , вычисляется по формуле 
. В нашем случае  , откуда  по таблице значений функции  получаем, что  , 
, то есть 
Значит интервал имеет вид 
Задачка сложноватая. Скажите, правильно ли она решена? и если да, то объясните, пожалуйста, откуда взялась эта формула ? Лапласа по другому выглядит, эту же нигде не нашёл, кучу учебников перерыл
(Сообщение отредактировал Sun Summer 26 окт. 2009 5:28)
(Сообщение отредактировал Sun Summer 26 окт. 2009 5:29)
(Сообщение отредактировал Sun Summer 26 окт. 2009 5:30)
(Сообщение отредактировал Sun Summer 26 окт. 2009 5:30)
(Сообщение отредактировал Sun Summer 26 окт. 2009 5:32)
|
Всего сообщений: 16 | Присоединился: октябрь 2009 | Отправлено: 26 окт. 2009 5:27 | IP
|
|
RKI 
Долгожитель
|
Цитата: Sun Summer написал 26 окт. 2009 5:27
Задача: Случайная величина X распределена нормально с математическим ожиданием а= 10 и средним квадратическим отклонением
. Найти интервал, в который с вероятностью 0,9973 попадет X в результате испытания.
Решение: Вероятность того, что абсолютная величина отклонения меньше положительного числа , вычисляется по формуле
. В нашем случае , откуда по таблице значений функции получаем, что ,
, то есть
Значит интервал имеет вид
Задачка сложноватая. Скажите, правильно ли она решена? и если да, то объясните, пожалуйста, откуда взялась эта формула ? Лапласа по другому выглядит, эту же нигде не нашёл, кучу учебников перерыл
Задача решена правильно.
Пусть случайная величина X распределена нормально с параметрами a (математическое ожидание) и 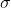 (среднее квадратическое отклонение).
Известно, что функция распределения случайной величины X имеет вид:
 = P(X<x) = 0.5 + \Phi (\frac{x-a}{\sigma}) )
Тогда
 = F(x_{2}) - F(x_{1}) = \Phi (\frac{x_{2}-a}{\sigma}) - \Phi (\frac{x_{1}-a}{\sigma}) )
Также известно, что функция Лапласа является нечетной, то есть
 = -\Phi (x) )
Следовательно,
 = P(-\delta < X-a < \delta) = P(a-\delta < X < a+\delta) = )
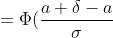 - \Phi (\frac{a-\delta - a}{\sigma}) = \Phi (\frac{\delta}{\sigma}) - \Phi (-\frac{\delta}{\sigma}) = )
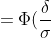 + \Phi (\frac{\delta}{\sigma}) = 2\Phi (\frac{\delta}{\sigma}) )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 26 окт. 2009 9:38 | IP
|
|
|
Форум
Решение задач по теории вероятности
