jlia0405
Новичок
|
   
Помогите пожалуйста!
независимые случай ные величины X и Y заданы следующими законами распределения:
х 0 2 4 6
р 0,1 0,2 0,3 0,4
у -1 1 3 5
р 0,2 0,3 0,3 0,2
составить законы распределения случайных величин Х+У, ХУ
Заранее огромное спасибо!
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 24 окт. 2009 16:10 | IP
|
|
RKI 
Долгожитель
|
Цитата: asselka написал 24 окт. 2009 14:54
2)Среди поступивших на сборку деталей 30% - с завода №1, остальные - с завода №2. Вероятность брака для завода №1 равна 0,02, для завода №2 - 0,03. Найти: а) вероятность того, что наугад взятая деталь стандартная; б) вероятность изготовления наугад взятой детали на заводе №1, если она оказалась стандартной.
H1 = {деталь с первого завода}
H2 = {деталь со второго завода}
P(H1) = 0.3
P(H2) = 1 - P(H1) = 1 - 0.3 = 0.7
A = {деталь стандартная}
A|H1 = {деталь стандартная при условии, что она с первого завода}
A|H2 = {деталь стандартная при условии, что она со второго завода}
P(A|H1) = 1 - 0.02 = 0.98
P(A|H2) = 1 - 0.03 = 0.97
а) По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) =
= (0.3)*(0.98) + (0.7)*(0.97) = 0.294 + 0.679 = 0.973
б) По формуле Байеса
P(H1|A) = P(H1)P(A|H1)/P(A) = (0.3)*(0.98)/(0.973) =
= (0.294)/(0.973) = 294/973 = 42/139
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 24 окт. 2009 16:27 | IP
|
|
RKI
Долгожитель
|
Цитата: potay написал 24 окт. 2009 12:10
№1
10 человек строятся в колонну в произвольном порядке. Какая вероятность того, что две определенные личности будут стоять рядом.
Посчитаем число n всевозможных исходов. Способов расставить 10 человек в колонну n = 10!
A = {два человека А и Б стоят рядом}
Посчитаем число m исходов, благоприятных событию A.
Если человек А стоит на первом месте, то человек Б может встать только на второе место, то есть только m1 = 1 альтернатива.
Если человек А стоит на десятом месте, то человек Б может встать только на девятое место, то есть только m2 = 1 альтернатива.
Если человек А стоит на одном из 8 мест (со второго по девятое), то человек Б может встать или до А, или после А. Таким образом, в этом случае альтернатив m3 = 8*2 = 16.
По правилу сложения m4 = m1 + m2 + m3 = 1 + 1 + 16 = 18.
Расставим остальных 8 человек. Расставить оставшихся 8 человек на 8 свободных позиций можно m5 = 8!.
По правилу произведения m = m4*m5 = 18*8!
По классическому определению вероятности
P(A) = m/n = (18*8!)/10! = 18/(9*10) = 0.2
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 24 окт. 2009 16:34 | IP
|
|
RKI
Долгожитель
|
Цитата: potay написал 24 окт. 2009 12:38
№3
Случайная величина Х имеет функцию распределения F(x). Найти вероятность попадания в интервал (А;B) цельность распределения; математическое ожидание, диспресию и среднее квадратичное отклонение. Построить графики функций распределения и плотности распределения.
{0 при x<=0
F(x) {sqrt(x^3) при 0<x<=1
{1 при x>1
F(x) = {0, x <= 0
{x^(3/2), 0 < x <= 1
{1, x > 1
f(x) = F'(x)
f(x) = {0, x <= 0
{(3/2)(x^(1/2)), 0 < x < 1
{0, x > 1
P(A < X < B) = F(B) - F(A)
 = \int\limits_{-\infty}^{+\infty} xf(x)dx = \int\limits_{-\infty}^{0} xf(x)dx + \int\limits_{0}^{1} xf(x)dx + \int\limits_{1}^{+\infty} xf(x)dx = )
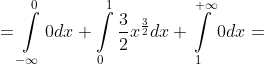
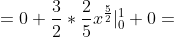
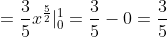
 = 0.6 )
 = \int\limits_{-\infty}^{+\infty} x^{2} f(x)dx = \int\limits_{-\infty}^{0} x^{2} f(x)dx + \int\limits_{0}^{1} x^{2} f(x)dx + \int\limits_{1}^{+\infty} x^{2} f(x)dx = )
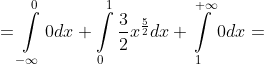
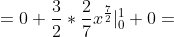
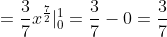
 = \frac{3}{7} )
 = M(X^{2}) - M^{2} (X) = \frac{3}{7} - \frac{9}{25} = \frac{12}{175} )
} = \sqrt{\frac{12}{175} } )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 24 окт. 2009 16:47 | IP
|
|
RKI
Долгожитель
|
Цитата: potay написал 24 окт. 2009 12:23
№2
Стрелок стреляет по цели, которая отдаляется. Вероятность попадания в нее в начале стрельбы равняется 0,8, а после каждого выстрела уменьшается на 0,1. Найти вероятность того что, стрелок попадет с третьего раза.
Ai = {стрелок попал с i-того раза}
P(A1) = 0.8
P(A2) = 0.7
P(A3) = 0.6
не Ai = {стрелок промахнулся при i-том выстреле}
P(не A1) = 1 - P(A1) = 1 - 0.8 = 0.2
P(не A2) = 1 - P(A2) = 1 - 0.7 = 0.3
A = {стрелок попал в цель с третьего раза}
A = (не A1)*(не A2)*A3
P(A) = P((не A1)*(не A2)*A3) = P(не A1)*P(не A2)*P(A3) =
= (0.2)*(0.3)*(0.6) = 0.036
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 24 окт. 2009 16:52 | IP
|
|
RKI
Долгожитель
|
Цитата: jlia0405 написал 24 окт. 2009 16:10
Помогите пожалуйста!
независимые случай ные величины X и Y заданы следующими законами распределения:
х 0 2 4 6
р 0,1 0,2 0,3 0,4
у -1 1 3 5
р 0,2 0,3 0,3 0,2
составить законы распределения случайных величин Х+У, ХУ
Заранее огромное спасибо!
Z = X + Y
{Z=-1} = {X=0, Y=-1}
{Z=1} = {X=2, Y=-1} + {X=0, Y=1}
{Z=3} = {X=4, Y=-1} + {X=2, Y=1} + {X=0, Y=3}
{Z=5} = {X=6, Y=-1} + {X=4, Y=1} + {X=2, Y=3} + {X=0, Y=5}
{Z=7} = {X=6, Y=1} + {X=4, Y=3} + {X=2, Y=5}
{Z=9} = {X=6, Y=3} + {X=4, Y=5}
{Z=11} = {X=6, Y=5}
P(Z=-1) = P(X=0, Y=-1) = P(X=0)P(Y=-1) = (0.1)*(0.2) = 0.02
P(Z=1) = P({X=2, Y=-1} + {X=0, Y=1}) =
= P(X=2, Y=-1) + P(X=0, Y=1) = P(X=2)P(Y=-1) + P(X=0)P(Y=1) =
= (0.2)*(0.2) + (0.1)*(0.3) = 0.04 + 0.03 = 0.07
P(Z=3) = P({X=4, Y=-1} + {X=2, Y=1} + {X=0, Y=3}) =
= P(X=4, Y=-1) + P(X=2, Y=1) + P(X=0, Y=3) =
= P(X=4)P(Y=-1) + P(X=2)P(Y=1) + P(X=0)P(Y=3) =
= (0.3)*(0.2) + (0.2)*(0.3) + (0.1)*(0.3) =
= 0.06 + 0.06 + 0.03 = 0.15
{Z=5} =
= P({X=6, Y=-1} + {X=4, Y=1} + {X=2, Y=3} + {X=0, Y=5}) =
= P(X=6, Y=-1) + P(X=4, Y=1) + P(X=2, Y=3) + P(X=0, Y=5) =
= P(X=6)P(Y=-1) + P(X=4)P(Y=1) + P(X=2)P(Y=3) + P(X=0)P(Y=5) =
= (0.4)*(0.2) + (0.3)*(0.3) + (0.2)*(0.3) + (0.1)*(0.2) =
= 0.08 + 0.09 + 0.06 + 0.02 = 0.25
P(Z=7) = P({X=6, Y=1} + {X=4, Y=3} + {X=2, Y=5}) =
= P(X=6, Y=1) + P(X=4, Y=3) + P(X=2, Y=5) =
= P(X=6)P(Y=1) + P(X=4)P(Y=3) + P(X=2)P(Y=5) =
= (0.4)*(0.3) + (0.3)*(0.3) + (0.2)*(0.2) =
= 0.12 + 0.09 + 0.04 = 0.25
P(Z=9) = P({X=6, Y=3} + {X=4, Y=5}) =
= P(X=6, Y=3) + P(X=4, Y=5) = P(X=6)P(Y=3) + P(X=4)P(Y=5) =
= (0.4)*(0.3) + (0.3)*(0.2) = 0.12 + 0.06 = 0.18
P(Z=11) = P(X=6, Y=5) = P(X=6)P(Y=5) = (0.4)*(0.2) = 0.08
Закон распределения случайной величины Z = X+Y имеет вид:
Z -1 1 3 5 7 9 11
P 0.02 0.07 0.15 0.25 0.25 0.18 0.08
Аналогично делается для случайной величины XY
(Сообщение отредактировал RKI 24 окт. 2009 17:16)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 24 окт. 2009 17:15 | IP
|
|
Natasha
Новичок
|
Помогите пожалуйста решить несколько задач. Нужны только ответы.
1. Пятерых учеников можно построить в шеренгу следующим числом способом: А) 5; Б) 5^5; В) 20; Г) 120
2. Какова вероятность из колоды в 36 карт вытянуть крестовую десятку?
3. В корзине 7 белых, 3 синих, 5 черных шаров. Какова вероятность вынуть первый и второй шар синими, а третий белым?
|
Всего сообщений: 25 | Присоединился: ноябрь 2008 | Отправлено: 24 окт. 2009 17:39 | IP
|
|
RKI
Долгожитель
|
Цитата: Natasha написал 24 окт. 2009 17:39
Помогите пожалуйста решить несколько задач. Нужны только ответы.
1. Пятерых учеников можно построить в шеренгу следующим числом способом: А) 5; Б) 5^5; В) 20; Г) 120
120
2. Какова вероятность из колоды в 36 карт вытянуть крестовую десятку?
1/36
3. В корзине 7 белых, 3 синих, 5 черных шаров. Какова вероятность вынуть первый и второй шар синими, а третий белым?
1/65
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 24 окт. 2009 17:51 | IP
|
|
potay
Новичок
|
RKI спасибо тебе большое
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 24 окт. 2009 18:30 | IP
|
|
Vorona
Новичок
|
 
я переписала условие задачи №1
1) Имеются шесть карточек разрезной азбуки с буквами Ш,А,Р,А,Д,А. Какова вер-ть того, что при расположении всех карточек в произвольном порядке на первом и в последнем местах будут нах-ся карточки с буквой А?
2) В партии из 30 деталей - 4 дефектных. Определить вероятность того, что среди 5 выбранных деталей окажутся дефектными хотя бы 2?
3) В первой урне 7 белых шаров и 3 черных, во второй - 4 белых и 5 черных. Из первой урны наугад вынули 2 шара и положили во вторую. Какого цвета шар теперь более вероятно вынуть из 2ой урны?
За ранее огромное спасибо)))
|
Всего сообщений: 7 | Присоединился: октябрь 2009 | Отправлено: 24 окт. 2009 20:13 | IP
|
|
|
Форум
Решение задач по теории вероятности
