RKI 
Долгожитель
|
   
Цитата: Vorona написал 23 окт. 2009 12:25
1) Имеются шесть карточек разрезной азбуки с буквами Ш,А,Р,А,Д,А. Какова вер-то того, что при расположении всех карточек в произвольном порядке на первом и в последних местах будут нах-ся карточки с буквой А?
Обратите внимание на выделенные мною слова.
Имеется в виду - на последних двух местах ИЛИ на первом и на последнем местах
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 23 окт. 2009 16:40 | IP
|
|
CryWolfy
Новичок
|
помогите пожалуйста решить задачки.в понедельник надо сдать уже.сам никак не допру.плз, оч надо!!!!
1) начерчены пять концентрических окружностей,радиусы которых равны соответственно kr (k = 1,2,3,4,5). Круг радиуса r и два кольца с внешними радиусами 3r и 4r заштрихованы.В круге радиуса 4r наудачу выбрана точка.Определить вероятность попадания этой точки:
a)в круг радиуса 2r
b)в заштрихованную область.
2) Учебник издан тиражом 100000 экземпляров. Вероятность того,что экземпляр учебника сброширован неправильн, равна 0,0001. Найти вероятность того,что
a)тираж содержит 5 бракованных книг.
b)по крайней мере 99998 книг сброшированы правильно.
|
Всего сообщений: 11 | Присоединился: октябрь 2009 | Отправлено: 23 окт. 2009 16:45 | IP
|
|
RKI
Долгожитель
|
Цитата: Vorona написал 23 окт. 2009 12:25
2) Устройство состоит из 2х независимо работающих элементов. Вероятность отказа первого = 0.3, вероятность отказа второго = 0.6. Найти вероятность того, что 1ый элемент не отказал, если известно, что отказал какой-то один из элементов.
Ai = {i-тый элемент отказал}, i=1,2
P(A1) = 0.3
P(A2) = 0.6
не Ai = {i-тый элемент не отказал}, i=1,2
P(не A1) = 1 - P(A1) = 1 - 0.3 = 0.7
P(не A2) = 1 - P(A2) = 1 - 0.6 = 0.4
A = {первый элемент не отказал}
B = {отказал какой-то один из элементов} =
= {первый элемент отказал, второй - нет ИЛИ второй элемент отказал, первый - нет}
B = A1*(не A2) + (не A1)*A2
P(B) = P(A1*(не A2) + (не A1)*A2) =
= P(A1*(не A2)) + P((не A1)*A2) =
= P(A1)P(не A2) + P(не A1)P(A2) =
= (0.3)*(0.4) + (0.7)*(0.6) = 0.12 + 0.42 = 0.54
AB = {первый элемент не отказал, а второй элемент отказал}
AB = (не A1)*A2
P(AB) = P((не A1)*A2) = P(не A1)*P(A2) =
= (0.7)*(0.6) = 0.42
A|B = {первый элемент не отказал при условии, что отказал какой-то один из элементов}
P(A|B) = P(AB)/P(B) = (0.42)/(0.54) = 42/54 = 7/9
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 23 окт. 2009 16:49 | IP
|
|
RKI
Долгожитель
|
Цитата: Maxgordon написал 23 окт. 2009 14:29
3. Ожидаемая рентабельность актива А равна 8% со средним квадратическим отклонением, равным 7%. Ожидаемая рентабельность актива В равна 11% и среднее квадратическое отклонение 10%. Корреляция между этими активами 0,7. Найдите ожидаемую доходность и среднее квадратическое отклонение портфеля, состоящего на 35% из А и на 65% из В.
Данная задача решена в разделе
Теория вероятностей в примерах
http://exir.ru/cgi-bin/ikonboard/topic.cgi?forum=7&topic=2182&start=560
задача 546
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 23 окт. 2009 17:01 | IP
|
|
RKI
Долгожитель
|
Цитата: CryWolfy написал 23 окт. 2009 15:30
В урне 5 белых и 6 черных шаров. Один из них утерян, причем неизвестно какой. Из урны подряд достали два шара и они оказались белыми. Найти вероятность того, что утерян белый шар.
H1 = {утерян белый шар}
H2 = {утерян черный шар}
P(H1) = 5/(5+6) = 5/11
P(H2) = 6/(5+6) = 6/11
A = {подряд достали два белых шара}
A|H1 = {подряд достали два белых шара, если был утерян белый шар} = {подряд достали два белых шара, если в урне остались 4 белых и 6 черных шаров}
P(A|H1) = (4/10)*(3/9) = 12/90
A|H2 = {подряд достали два белых шара, если был утерян черный шар} = {подряд достали два белых шара, если в урне остались 5 белых и 5 черных шаров}
P(A|H2) = (5/10)*(4/9) = 20/90
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) =
= (5/11)*(12/90) + (6/11)*(20/90) =
= 60/990 + 120/990 = 180/990
По формуле Байеса
P(H1|A) = P(H1)P(A|H1)/P(A) =
= (5/11)*(12/90)/(180/990) = (60/990)/(180/990) =
= 60/180 = 1/3
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 23 окт. 2009 17:22 | IP
|
|
RKI
Долгожитель
|
Цитата: CryWolfy написал 23 окт. 2009 16:45
2) Учебник издан тиражом 100000 экземпляров. Вероятность того,что экземпляр учебника сброширован неправильн, равна 0,0001. Найти вероятность того,что
a)тираж содержит 5 бракованных книг.
b)по крайней мере 99998 книг сброшированы правильно.
n = 100 000 - количество учебников
p = 0.0001
np = 100000*(0.0001) = 10
m - число бракованных книг
100000-m - число качественных книг
а)
 = \frac{10^{5} e^{-10} }{5!} = )
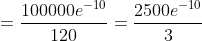
б)
 = P(m <= 2) = )
 + P(m=1) + P(m=2) = )
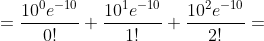
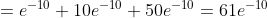
(Сообщение отредактировал RKI 23 окт. 2009 17:36)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 23 окт. 2009 17:35 | IP
|
|
RKI
Долгожитель
|
Цитата: CryWolfy написал 23 окт. 2009 16:45
1) начерчены пять концентрических окружностей,радиусы которых равны соответственно kr (k = 1,2,3,4,5). Круг радиуса r и два кольца с внешними радиусами 3r и 4r заштрихованы.В круге радиуса 4r наудачу выбрана точка.Определить вероятность попадания этой точки:
a)в круг радиуса 2r
b)в заштрихованную область.
Пространство всевозможных исходов - круг C радиуса 4r.
S(C) = П(4r)^2 = 16П(r^2)
а) A = {точка попала в круг радиуса 2r} - круг радиуса 2r.
S(A) = П(2r)^2 = 4П(r^2)
По геометрическому определению вероятности
P(A) = S(A)/S(C) = 4П(r^2)/16П(r^2) = 4/16 = 0.25
б) B = {точка попала в заштрихованную область}
S(B) = 13П(r^2)
P(B) = S(B)/S(C) = 13П(r^2)/16П(r^2) = 13/16 = 0.8125
P.S. Данная задача на геометрическую вероятность, поэтому вся ее суть - сделать чертеж и правильно вычислить соответствующие площади
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 23 окт. 2009 17:48 | IP
|
|
CryWolfy
Новичок
|
RKI спасибо большое ты просто МЕГО-ЧЕЛОВЕК!!!помогаешь тут всем безкорыстно.ОГРОМНЕЙШЕЕ СПАСИБО ТЕБЕ!!!!
|
Всего сообщений: 11 | Присоединился: октябрь 2009 | Отправлено: 23 окт. 2009 18:32 | IP
|
|
Zardinag
Новичок
|
RKI, спасибо вам огромное, дай бог вам здоровья.
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 23 окт. 2009 20:57 | IP
|
|
blendas
Новичок
|
--------------------------------------------------------------------------------
Цитата: blendas написал 23 окт. 2009 1:23
По данным опроса общественного мнения, из 10800 зарегистрированных избирателей 45% собираются проголосовать за либеральную партию. Если все, кто имеет право голосовать, придут на избирательные участки и данные опроса объективны, то какова вероятность, что либеральная партия получит менее 5000 голосов?
--------------------------------------------------------------------------------
n = 10 800 - количество избирателей
p = 0.45 - вероятность того, что избиратель проголосует за либеральную партию
q = 1 - p = 1 - 0.45 = 0.55
np = 10800*(0.45) = 4860
npq = 10800*(0.45)*(0.55) = 2673
m - количество голосов, которые получит либеральная партия
,
,
,
0,5+Ф(2,71) =0,5+0,4965 =0,9965
Благодарности нет предела, ты просто суперчеловечище, подскажи еще как найти число Ф?
|
Всего сообщений: 10 | Присоединился: октябрь 2009 | Отправлено: 23 окт. 2009 21:51 | IP
|
|
|
Форум
Решение задач по теории вероятности
