Irochkacat
Новичок
|
   
Здравствуйте, помогите пожалуйста решить две задачки, а то завтра здавать, а ничего не понимаю(((
1. на сборку поступило десять деталей, среди которых четыре бракованные. Сборщик наудачу берет три детали.найти вероятности событий:
А- взятые детали стандартные
В-только одна деталь среди взятых стандартная
С-хотя бы одна из взятых деталей стандартная.
2. Случайная величина распределена по нормальному закону с математическим ожиданием m=3. Р{Х<3}=0,15. найти ее дисперсию,вычислить вероятность отрицательных значений случайной величины.
ЗАРАНЕЕ ОГРОМНОЕ СПАСИБО!
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 23 окт. 2009 0:29 | IP
|
|
blendas
Новичок
|
помогите, плиз...
По данным опроса общественного мнения, из 10800 зарегистрированных избирателей 45% собираются проголосовать за либеральную партию. Если все, кто имеет право голосовать, придут на избирательные участки и данные опроса объективны, то какова вероятность, что либеральная партия получит менее 5000 голосов?
|
Всего сообщений: 10 | Присоединился: октябрь 2009 | Отправлено: 23 окт. 2009 1:23 | IP
|
|
RKI 
Долгожитель
|
Цитата: Zardinag написал 22 окт. 2009 22:12
1) Устройство состоит из большего числа независимо работающих элементов с одинаковой(очень малой) вероятностью отказа каждого элемента за время Т. Найти среднее число отказавших за время Т элементов, если вероятность того, что за это время откажет хотя бы один элемент, равна 0,99. Т не дано(т.е. на ваше усмотрение похоже).
n - число независимо работающих элементов (достаточно большое)
p - вероятность отказа отдельно взятого элемента за время T (достаточно малая)
Пусть случайная величина X - число отказавших за время T элементов.
Данная случайная величина подчиняется закону Пуассона с параметром
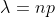
Известно, что
 = \lambda )
Найдем значение данного параметра.
По условию задачи P(X >= 1) = 0.99.
С другой стороны,
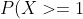 = 1 - P(X < 1) = 1 - P(X=0) = )
 )
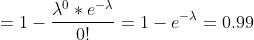
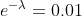
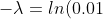 = \lambda = - \ln(0.01) = ln(100) )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 23 окт. 2009 9:25 | IP
|
|
Vorona
Новичок
|
  
1) Имеются шесть карточек разрезной азбуки с буквами Ш,А,Р,А,Д,А. Какова вер-то того, что при расположении всех карточек в произвольном порядке на первом и в последних местах будут нах-ся карточки с буквой А?
2) Устройство состоит из 2х независимо работающих элементов. Вероятность отказа первого = 0.3, вероятность отказа второго = 0.6. Найти вероятность того, что 1ый элемент не отказал, если известно, что отказал какой-то один из элементов. Спасибо))
|
Всего сообщений: 7 | Присоединился: октябрь 2009 | Отправлено: 23 окт. 2009 12:25 | IP
|
|
Maxgordon
Новичок
|
 
Здравствуйте помогите пожалуйста решить задачки завал полный ко вторнику нужно. Заранее благодарен.
Задача 1.
Предполагая, что вероятность поражения мишени при одном выстреле равна 0,6, найти вероятности следующих событий: 1) при 12 выстрелах мишень будет поражена 7 раз; 2) при 200 выстрелах цель будет поражена не менее 1 И, но не более 130; 3) при 200 выстрелах мишень будет поражена не более 110 раз; 4) при 200 выстрелах мишень будет поражена ровно 115 раз.
|
Всего сообщений: 2 | Присоединился: октябрь 2009 | Отправлено: 23 окт. 2009 14:27 | IP
|
|
Maxgordon
Новичок
|
Задача 2 и 3
2. Инвестор имеет возможность составить портфель из трех видов некоррелированных бумаг, эффективности ej и риски gj которых даны в таблице. Рассмотрите все варианты составления ~ портфеля из этих бумаг равными долями. Дайте графическое изображение всех этих портфе- ~ лей точками (по осям координат — эффективность, риск). Есть ли точки, оптимальные по
3. Ожидаемая рентабельность актива А равна 8% со средним квадратическим отклонением, равным 7%. Ожидаемая рентабельность актива В равна 11% и среднее квадратическое отклонение 10%. Корреляция между этими активами 0,7. Найдите ожидаемую доходность и среднее квадратическое отклонение портфеля, состоящего на 35% из А и на 65% из В.
|
Всего сообщений: 2 | Присоединился: октябрь 2009 | Отправлено: 23 окт. 2009 14:29 | IP
|
|
CryWolfy
Новичок
|
Здраствуйте.
В урне 5 белых и 6 черных шаров. Один из них утерян, причем неизвестно какой. Из урны подряд достали два шара и они оказались белыми. Найти вероятность того, что утерян белый шар.
Убей бох не пойму как это решить, и гипотезы примерял, и Бейеса - неполучается. Помогите, пожжалуйста.
|
Всего сообщений: 11 | Присоединился: октябрь 2009 | Отправлено: 23 окт. 2009 15:30 | IP
|
|
RKI
Долгожитель
|
Цитата: Irochkacat написал 23 окт. 2009 0:29
1. на сборку поступило десять деталей, среди которых четыре бракованные. Сборщик наудачу берет три детали.найти вероятности событий:
А- взятые детали стандартные
В-только одна деталь среди взятых стандартная
С-хотя бы одна из взятых деталей стандартная.
Посчитаем число n всевозможных исходов.
Способов выбрать 3 детали из 10 имеющихся
n = C(3;10) = 10!/3!7! = 120
а) A = {взятые 3 детали стандартные}
Посчитаем число m исходов, благоприятных событию A. Стандартных деталей 10 - 4 = 6. Способов выбрать 3 детали из 6 имеющихся стандартных:
m = C(3;6) = 6!/3!3! = 20
По классическому определению вероятности
P(A) = m/n = 20/120 = 1/6
б) B = {только одна деталь из взятых трех стандартная}
Посчитаем число k исходов, благоприятных событию B.
Способов выбрать 1 деталь из 6 имеющихся стандартных
k1 = C(1;6) = 6!/1!5! = 6.
Способов выбрать 2 детали из 4 имеющихся бракованных
k2 = C(2;4) = 4!/2!2! = 6.
По правилу произведения
k = k1*k2 = 6*6 = 36
По классическому определению вероятности
P(B) = k/n = 36/120 = 3/10
в) C = {хотя бы одна из взятых деталей стандартная}
не C = {все три детали бракованные}
Посчитаем число l исходов, благоприятных событию не C.
Способов выбрать 3 детали из 4 имеющихся дефектных
l = C(3;4) = 4!/3!1! = 4
По классическому определению вероятности
P(не C) = l/n = 4/120 = 1/30
P(C) = 1 - P(не C) = 1 - 1/30 = 29/30
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 23 окт. 2009 16:24 | IP
|
|
RKI
Долгожитель
|
Цитата: Irochkacat написал 23 окт. 2009 0:29
2. Случайная величина распределена по нормальному закону с математическим ожиданием m=3. Р{Х<3}=0,15. найти ее дисперсию,вычислить вероятность отрицательных значений случайной величины.
Проверьте условия задачи
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 23 окт. 2009 16:29 | IP
|
|
RKI
Долгожитель
|
Цитата: blendas написал 23 окт. 2009 1:23
По данным опроса общественного мнения, из 10800 зарегистрированных избирателей 45% собираются проголосовать за либеральную партию. Если все, кто имеет право голосовать, придут на избирательные участки и данные опроса объективны, то какова вероятность, что либеральная партия получит менее 5000 голосов?
n = 10 800 - количество избирателей
p = 0.45 - вероятность того, что избиратель проголосует за либеральную партию
q = 1 - p = 1 - 0.45 = 0.55
np = 10800*(0.45) = 4860
npq = 10800*(0.45)*(0.55) = 2673
m - количество голосов, которые получит либеральная партия
 = 0.5 + \Phi (\frac{5000 - 4860}{\sqrt{2673} }) \sim )
 \sim 0.5 + 0.4965 = 0.9965 )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 23 окт. 2009 16:36 | IP
|
|
|
Форум
Решение задач по теории вероятности
