Drank

Новичок
|
    
RKI, спасибо вам большое. Пожалуйста, помогите с еще одной задачкой...
Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,001. Найти вероятность того, что среди 250 деталей окажется ровно 5 бракованных. Определить закон распределения СВ X и ее числовые характеристики.
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 18 окт. 2009 17:10 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: KuziaaCat написал 18 окт. 2009 16:59
1) HCB задана дифференциальной функцией f(x):
f(x)={0 при x<-(пи/2) или х>0,
{cosx при -(пи/2)<x<0
a) Найти функцию распределения CB X: F(x)
б) Найти вероятность попадания CB X в интервал (-(пи/3);-(пи/4))
f(x) = {0, x < -П/2
{cosx, -П/2 < x < 0
{0, x > 0
 = \int\limits_{-\infty}^{x} f(t)dt )
Если 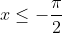 , то , то
 = \int\limits_{-\infty}^{x} f(t)dt = \int\limits_{-\infty}^{x} 0dt = 0 )
Если 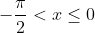 , то , то
 = \int\limits_{-\infty}^{x} f(t)dt = \int\limits_{-\infty}^{-\frac{\pi}{2} } f(t)dt + \int\limits_{-\frac{\pi}{2} }^{x} f(t)dt = \int\limits_{-\infty}^{-\frac{\pi}{2} } 0dt + \int\limits_{-\frac{\pi}{2} }^{x} (cost)dt = )
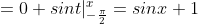
Если 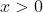 , то , то
 = \int\limits_{-\infty}^{x} f(t)dt = \int\limits_{-\infty}^{-\frac{\pi}{2} } f(t)dt + \int\limits_{-\frac{\pi}{2} }^{0} f(t)dt + \int\limits_{0}^{x} f(t)dt = )
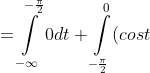dt + \int\limits_{0}^{x} 0dt = 0 + sint |_{-\frac{\pi}{2} }^{0} + 0 = 1 )
F(x) = {0, x <= -П/2
{sinx+1, -П/2 < x <= 0
{1, x > 0
 = F(-\frac{\pi}{4}) - F(-\frac{\pi}{3}) = sin(-\frac{\pi}{4}) + 1 - sin(-\frac{\pi}{3}) - 1 = )
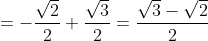
(Сообщение отредактировал RKI 18 окт. 2009 17:36)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 окт. 2009 17:23 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: KuziaaCat написал 18 окт. 2009 16:59
2) Дана интегральная функция HCB X:
{0 при x<=0
F(x)={sin2x при 0<x<=(пи/4)
{1 при х>(пи/4)
Найти дифференциальную функцию и вероятность попадания CB на интервал (пи/16;пи/8).
F(x) = {0, x <= 0
{sin2x, 0 < x <= П/4
{1, x > П/4
f(x) = F'(x)
f(x) = {0, x < 0
{2cos2x, 0 < x <= П/4
{0, x > П/4
 = F(\frac{\pi}{8}) - F(\frac{\pi}{16}) = )
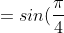 - sin(\frac{\pi}{8}) = \frac{\sqrt{2} }{2} - \frac{2 - \sqrt{2} }{4} = \frac{3\sqrt{2} - 2}{4} )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 окт. 2009 17:45 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Drank написал 18 окт. 2009 17:10
Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,001. Найти вероятность того, что среди 250 деталей окажется ровно 5 бракованных. Определить закон распределения СВ X и ее числовые характеристики.
n = 250 - количество деталей
p = 0.001 - вероятность того, что деталь бракованная
np = 250*(0.001) = 0.25
m - количество бракованных деталей
P(m=5) = ((0.25)^5)(e^(-0.25))/5! - можно примерно посчитать на калькуляторе
По сути задачи не ясно, что описывает случайная величина X
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 окт. 2009 17:50 | IP
|
|
Elocloire


Новичок
|
     
Спасибо RKI 
|
Всего сообщений: 6 | Присоединился: октябрь 2009 | Отправлено: 18 окт. 2009 17:54 | IP
|
|
Zardinag


Новичок
|
     
Здравствуйте, помогите пожалуйста решить несколько задач по ТВ:
1. Устройство состоит из большего числа независимо работающих элементов с одинаковой(очень малой) вероятностью отказа каждого элемента за время Т. Найти среднее число отказавших за время Т элементов, если вероятность того, что за это время не откажет хотябы один элемент, равна 0,99. Т не дано(т.е. на ваше усмотрение похоже).
2. Из 25 контрольных работ, среди которых 5 оценены на "отлично", наугад извлекаются 3 работы. Найти закон распределения ДСВ X, если X - число работ, оцененных на "отлично" среди извлеченных. Построить многоугольник(?) распределения. Чему равна вероятность событий X>0?
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 18 окт. 2009 18:07 | IP
|
|
KuziaaCat


Новичок
|
     
RKI, спасибо огромное, чтобы я без вас делал.
|
Всего сообщений: 6 | Присоединился: октябрь 2009 | Отправлено: 18 окт. 2009 18:07 | IP
|
|
vikycik

Новичок
|
    
RKI извините я не поняла какой ответ в 57?
В 62 10 часов.
В 67 правильно записана функция. Есть варианты ответов:
1) x 0 1 4 8
p 0,3 0,4 0,6 1
2)x 1 4 8
p 0 0,3 0,4
3) x 1 4 8
p 0,3 0,1 0,6
|
Всего сообщений: 34 | Присоединился: сентябрь 2009 | Отправлено: 18 окт. 2009 18:11 | IP
|
|
vikycik

Новичок
|
    
И помогите пожалуйста с этими заданиями:
72. Известно, дисперсия D(C+X)=4 . Тогда постоянная С равна:
Варианты ответов:
1) 1 2) 2 3)3 3)любое действительное число
75. СВ Н задана законом распределения :
H 1 2 3
p 1/2 1/4 1/4
Дисперсия равна:
1)1 2)3/4 3) 3/16 4)3/2
76. Математическое ожидание СВ Х равно 4. Математическое ожидание отклонения этой величины равно:
Варианты ответов:
1) 0 2) 1 3)2 4) 4
77. Приобрели 20 билетов, причем вероятность выигрыша по одному билету равна 0,4. Математическое ожидание числа лотерейных билетов, на которые выпадут выигрыши, равно
Варианты ответов:
1) 50 2) 0,4 3)4 4) 8
78. Известно, что вероятность события А равна р. Математическое ожидание числа появлений события А в одном испытании равна
Варианты ответов:
1) 0 2) 1 3) p 4) g=1-р
|
Всего сообщений: 34 | Присоединился: сентябрь 2009 | Отправлено: 18 окт. 2009 18:19 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: vikycik написал 18 окт. 2009 18:11
RKI извините я не поняла какой ответ в 57?
(1)
В 67 правильно записана функция. Есть варианты ответов:
1) x 0 1 4 8
p 0,3 0,4 0,6 1
2)x 1 4 8
p 0 0,3 0,4
3) x 1 4 8
p 0,3 0,1 0,6
обратите внимание на границы в функции
указанная вами функция ВООБЩЕ не является функцией распределения
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 окт. 2009 18:32 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности