RKI 
Долгожитель
|
   
Цитата: Anelka написал 18 окт. 2009 11:40
Помогите, пож-та, решить задачку.
Случайная величина x распределена с параметрами a=6, s=17. С точностью 2 знака после запятой найти Р(5x-144>0)
Заранее большое спасибо!!!
 = P(X > 28.8) = 0.5 - \Phi (\frac{28.8 - 6}{17}) \sim )
 \sim 0.5 - 0.4099 = 0.0901 )
(Сообщение отредактировал RKI 18 окт. 2009 15:17)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 окт. 2009 15:16 | IP
|
|
RKI
Долгожитель
|
Цитата: vikycik написал 18 окт. 2009 2:38
55. СВ Х подчиняется равномерному распределению в интервале (0;1) . Вероятность попадания величины Х в результате испытания в интервал (с;к) , принадлежащий интервалу (0;1), равна
Варианты ответов:
1) 1 2) к-с 3) с-к 4) 0
f(x) = {0, x <= 0
{1, 0 < x < 1
{0, x >= 1
 = \int\limits_{c}^{k} f(x)dx = \int\limits_{c}^{k} dx = k - c )
57. Случайная величина Х задана функцией распределения
F(x)={0 при x<=0
{x при 0<x<=1
{1 при x>0
Плотность распределения f(x) этой величины на интервале (0;1) равна:
Варианты ответов:
1) 1 2) 0 3)(x^2/2) - 1/2 4) x^2/2
F(x) = {0, x <= 0
{x, 0 < x <= 1
{1, x > 1
f(x) = F'(x)
f(x) = {0, x < 0
{1, 0 < x < 1
{0, x > 1
58. Известно, что интеграл(от b до a)Cdx=1. Тогда С равно:
Варианты ответов:
1) 1 2) 1/b-a 3) 1/ интеграл(от b до a)dx 4) f(x) 5) 0
 = 1 )
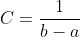
59. f(x) является функцией плотности нормального распределения некоторой случайной величины. Сколько утверждений из числа перечисленных являются справедливыми в любом случае? 1) f(x)непрерывна справа; 2) предел f(x)=0 при неограниченном возрастании x по абсолютной величине ; 3) при x=a =М(x ) функция имеет максимум ; 4) f(x) строго монотонна на всей числовой прямой; 5) при всех значениях x функция принимает положительные значения.
Варианты ответов:
1) 0 2) 1 3) 2 4) 3 5) 4 6) 5
Верны утверждения под номерами: 2; 3; 4; 5
60. СВ Х распределена по нормальному закону. Математическое ожидание и среднее квадратическое отклонение этой величины соответственно равны 30 и 10. Вероятность того, что Х примет значение, принадлежащее интервалу(10;50) равна:
Варианты ответов:
1) 2Ф(2) 2) 0 3)Ф(50-30/10)-Ф(10-30/10)
4) 1/2 (Ф(50-30/10*корень из 2)-Ф(10-30/10*корень из 2))
 = \Phi (\frac{50 - 30}{10}) - \Phi (\frac{10 - 30}{10}) = )
 - \Phi (-2) = \Phi (2) + \Phi (2) = 2\Phi (2) )
62. Время безотказной работы элемента распределено по показательному закону f(t)=0,02e^-0,02t при t>=0. Вероятность того, что элемент проработает безотказно 10 часов равна:
Варианты ответов:
1)1- e^-2 2)e^-2 3)0,02e^-2 4)1-0,02e^-2
10 или 100 часов?
63. Непрерывная СВ Х распределена по показательному закону f(x)=5e^-5x (x>=0),f(x)=0 (x<0) . Вероятность того, что в результате испытания Х попадет в интервал (0;1) равна
Варианты ответов:
1) 1 2) 5e^-5 3)e^-5 4)1-e^-5
 = \int\limits_{0}^{1} f(x)dx = \int\limits_{0}^{1} 5e^{-5x} dx = )
66. Плотность вероятности СВ Х имеет вид
f(x)={ 0 при x<=0
{2x при 0<x<=1
{0 при x>0
Вероятность того, что в результате испытания Х примет значение, принадлежащее интервалу(3/4;1) , равна
Варианты ответов:
1)9/16 2)3/4 3) 7/16 4)1/4
 = \int\limits_{\frac{3}{4} }^{1} f(x)dx = \int\limits_{\frac{3}{4} }^{1} 2xdx = )
67. Функция распределения имеет вид:
f(x)={ 0 при x<=1
{0,3 при 0<x<=1
{0,4 при 4<x<=8
{1 при x>8
Какой вид будет иметь таблица распределения ДСВ Х?
Запишите внимательно функцию
68. СВ Х задана функцией распределения:
f(x)={ 0 при x<=-1
{(x/3)+(1/3) при -1<x<=2
{1 при x>2
В результате испытания Х примет значение, заключенное в интервале (0;1) :
Варианты ответов:
1)1/3 2)2/3 3)3/3 4)нет правильного ответа
 = F(1) - F(0) = \frac{2}{3} - \frac{1}{3} = \frac{1}{3} )
(Сообщение отредактировал RKI 18 окт. 2009 15:44)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 окт. 2009 15:43 | IP
|
|
RKI
Долгожитель
|
Цитата: vikycik написал 18 окт. 2009 2:38
69. Вероятность того, что непрерывная СВ Х примет одно определенное значение равна :
Варианты ответов:
1) 1 2) 0 3)1/2 4) этому значению
(2)
70. Сравнили дисперсию D(C) и математическое ожидание M(C) , где С =const. Результат сравнения получился следующим:
Варианты ответов:
1)D(C)<M(C) 2)D(C)>M(C) 3)D(C)=M(C)
4)характеристики сравнивать нельзя
M(C) = C
D(C) = 0
Сравнить невозможно, так как неизвестен знак константы C
71. Известно, дисперсия D(CY)=8 и дисперсия D(Y)=2 . Тогда постоянная С равна:
Варианты ответов:
1) 1 2) 2 3) 3 3)любое действительное число
D(CY) = (C^2)D(Y) = 2(C^2) = 8
C^2 = 4
C = 2
72. Известно, дисперсия D(C+X)=4 . Тогда постоянная С равна:
Варианты ответов:
1) 1 2) 2 3)3 3)любое действительное число
D(X+C) = DX
Поэтому C может быть любым действительным числом
73. Дисперсия разности двух независимых случайных величин D(X-Y) равна:
Варианты ответов:
1) D(X)-D(Y) 2)D(X)+D(Y) 3) постоянной С 4)0
D(X-Y) = D(X) + D(-Y) = D(X) + D(Y)
(Сообщение отредактировал RKI 18 окт. 2009 15:57)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 окт. 2009 15:56 | IP
|
|
RKI
Долгожитель
|
Цитата: Alessia написал 18 окт. 2009 11:31
По самолёту производится 2 последовательных независимых выстрелов. Вероятность попадения при 1 выстреле равна 0,5, вероятность попадения при 2 выстреле равна 0,2. При попадании в самолёт 1 снаряда он выходит из строя с вероятностью 0,25, а при попадании 2 снарядов с вероятностью 0,5.
1) Определить вероятность вывода самолёта из строя в рез-те 2 выстрелов.
2)в рез-те 2 выстрелов самолёт не был выведен из строя. Найти вероятность того,что в самолёт произошло 2 попадания.
H0 = {нет попаданий в самолет}
H1 = {одно попадание в самолет}
H2 = {два попадания в самолет}
P(H0) = (1-0.5)*(1-0.2) = (0.5)*(0.8) = 0.4
P(H1) = (1-0.5)*(0.2) + (0.5)*(1-0.2) = (0.5)*(0.2) + (0.5)*(0.8) =
= 0.1 + 0.4 = 0.5
P(H2) = (0.5)*(0.2) = 0.1
A = {самолет сбит}
A|H0 = {самолет сбит, если попаданий нет}
A|H1 = {самолет сбит при одном попадании}
A|H2 = {самолет сбит при двух попаданиях}
P(A|H0) = 0
P(A|H1) = 0.25
P(A|H2) = 0.5
1) По формуле полной вероятности
P(A) = P(H0)P(A|H0) + P(H1)P(A|H1) + P(H2)P(A|H2) =
= (0.4)*0 + (0.5)*(0.25) + (0.1)*(0.5) =
= 0 + 0.125 + 0.05 = 0.175
2) не A = {самолет не был выведен из строя}
P(не A) = 1 - P(A) = 1 - 0.175 = 0.825
P(не A|H2) = 1 - P(A|H2) = 1 - 0.5 = 0.5
По формуле Байеса
P(H2|не A) = P(H2)P(не A|H2)/P(A) = (0.1)*(0.5)/(0.825) =
= (0.05)/(0.825) = 2/33
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 окт. 2009 16:13 | IP
|
|
Alessia
Новичок
|
RKI ,спасибо большое Вам за вашу помощь! Я очень признательна и благодарна Вам!
Попробую сейчас разобрать эту задачу получше.
(Сообщение отредактировал Alessia 18 окт. 2009 19:41)
|
Всего сообщений: 8 | Присоединился: октябрь 2009 | Отправлено: 18 окт. 2009 16:20 | IP
|
|
Drank
Новичок
|
Помогите пожалуйста разобраться с задачами. Никак не получается решить =(
1) Найти M(Х) числа лотерейных билетов, на которые выпадут выйгрыши, если приобретено 50 билетов, причем вероятность выйгрыша равна 0,01.
2) Производится 20 независимых испытаний, в каждом из которых вероятность появления успеха равна 0,2. Найти дисперсию числа появления успеха в этих испытаниях.
Заранее большое спасибо!
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 18 окт. 2009 16:24 | IP
|
|
RKI
Долгожитель
|
Цитата: Drank написал 18 окт. 2009 16:24
1) Найти M(Х) числа лотерейных билетов, на которые выпадут выйгрыши, если приобретено 50 билетов, причем вероятность выйгрыша равна 0,01.
Случайная величина X - число выигрышных билетов среди 50 имеющихся.
n = 50 - количество лотерейных билетов
p = 0.01 - вероятность того, что билет выигрышный
Случайная величина X имеет распределение Бернулли с параметрами n = 50 и p = 0.01.
M(X) = np = 50*(0.01) = 0.5
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 окт. 2009 16:35 | IP
|
|
RKI
Долгожитель
|
Цитата: Drank написал 18 окт. 2009 16:24
2) Производится 20 независимых испытаний, в каждом из которых вероятность появления успеха равна 0,2. Найти дисперсию числа появления успеха в этих испытаниях.
Случайная величина X - число появлений успеха при 20 независимых испытаниях.
n = 20 - количесвто независимых испытаний
p = 0.2 - вероятность успеха при одном испытании
q = 1 - p = 1 - 0.2 = 0.8
Случайная величина X имеет распределение Бернулли с параметрами n = 20 и p = 0.2
D(X) = npq = 20*(0.2)*(0.8) = 3.2
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 окт. 2009 16:37 | IP
|
|
RKI
Долгожитель
|
Цитата: KuziaaCat написал 18 окт. 2009 14:17
В партии из 10 деталей имеется 8 стандартных. Из этой партии на удачу взято 2 детали. Найти закон распределения случайной величины Х, равный числу стандартных деталей в выборке. Построить многоугольник распределения.
Случайная величина X - число стандартных деталей среди 2 выбранных.
Данная случайная величина может принимать следующие значения:
{X=0} - две детали бракованные
{X=1} - одна деталь - бракованная и одна деталь - стандартная
{X=2} - две детали - стандартные
P(X=0) = C(2;2)/C(2;10) = 1/45
P(X=1) = C(1;2)C(1;8)/C(2;10) = 2*8/45 = 16/45
P(X=2) = C(2;8)/C(2;10) = 28/45
Закон распределения случайной величины X имеет вид:
X 0 1 2
P 1/45 16/45 28/45
Многоугольник распределения - ломаная, отрезки которой соединяют точки (0; 1/45), (1; 16/45) и (2; 28/45)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 18 окт. 2009 16:43 | IP
|
|
KuziaaCat
Новичок
|
RKI, спасибо вам огромное за помощь! Можете посмотреть пожалуйста еще пару задач, очень прошу:
1) HCB задана дифференциальной функцией f(x):
f(x)={0 при x<-(пи/2) или х>0,
{cosx при -(пи/2)<x<0
a) Найти функцию распределения CB X: F(x)
б) Найти вероятность попадания CB X в интервал (-(пи/3);-(пи/4))
2) Дана интегральная функция HCB X:
{0 при x<=0
F(x)={sin2x при 0<x<=(пи/4)
{1 при х>(пи/4)
Найти дифференциальную функцию и вероятность попадания CB на интервал (пи/16;пи/8).
Заранее огромное спасибо!
|
Всего сообщений: 6 | Присоединился: октябрь 2009 | Отправлено: 18 окт. 2009 16:59 | IP
|
|
|
Форум
Решение задач по теории вероятности
