vikycik

Новичок
|
    
Привет помогите подготовится к тесту по тв:
2 Время ожидания автобуса есть равномерно распределенная на отрезке [0,12] случайная величина Х. Найти среднее время ожидания автобуса.
Варианты ответов:
1)0 2)3 3)6 4)0,5 5)12
6. Из следующих пар событий совместными являются:
Варианты ответов:
1) А1 = {выход из строя телевизора работающего в гостиной}, В1 = {на кухне};
2) А2 = {попадание при одном выстреле}, В2 = {промах};
3) А3 = {хотя бы одно попадание при двух выстрелах}; В3 = {два попадания}.
4) А4 = {в магазин вошел покупатель старше 60 лет}; B4 = {в магазин вошла Елена Сергеевна};
5) А5 = {появление герба на первой монете}; В5 ={появление числа на второй монете}.
3 Плотность вероятности f(x) равномерно распределенной случайной величины Х сохраняет на отрезке [3; 7] постоянное значение, равное h.; вне этого интервала плотность вероятности равна нулю. Найти h.
Варианты ответов:
1)1/3 2)1 3)1/2 4)1/4 5)2
21. В группе 25 студентов, из которых отлично учится 5 человек, хорошо- 12, удовлетворительно- 6 и слабо-2. Преподаватель вызывает студента. Какова вероятность того, что вызванный студент или отличник или хорошист?
Варианты ответов:
1) 0,85 2) 8/25 3) 17/25 4) 0,5 5) 0,3
22. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие, окажется высшего сорта равна 0,8. Найдите вероятность того, что из трех проверенных изделий только два высшего сорта.
Варианты ответов:
1)0,384 2)0,53)0,3 4) 0,4 5)0,616
23. Вероятность для компании, занимающейся строительством терминалов для аэропортов, получить контракт в стране А равна 0,4, вероятность выиграть его в стране В равна 0,3. Вероятность того, что контракты будут заключены и в стране А, и в стране В, равна 0,12. Чему равна вероятность того, что компания получит контракт хотя бы в одной стране?
Варианты ответов:
1)0,58 2)0,82 3)0,22 4)0,02 5)0,5
|
Всего сообщений: 34 | Присоединился: сентябрь 2009 | Отправлено: 12 окт. 2009 1:50 | IP
|
|
Kataryna

Новичок
|
     
Доброе время суток! Будьте добры, помогите, пожалуйста, решить задачку:
В коробке 7 шоколадок, 10 ирисок, 5 вафельных конфет. Девочка подходит к коробке, берёт одну конфету, затем вторую конфету, затем третью конфету. Какая вероятность того, что:
1) съеденные конфеты одинаковые;
2) съеденные конфеты разные?
Если можно, подскажите, пожалуйста, хотя бы формулу.
Заранее ОЧЕНЬ БЛАГОДАРНА!!!!!!!!!
|
Всего сообщений: 42 | Присоединился: декабрь 2008 | Отправлено: 12 окт. 2009 9:52 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: vikycik написал 12 окт. 2009 1:50
Привет помогите подготовится к тесту по тв:
2 Время ожидания автобуса есть равномерно распределенная на отрезке [0,12] случайная величина Х. Найти среднее время ожидания автобуса.
Варианты ответов:
1)0 2)3 3)6 4)0,5 5)12
M(X) = (0+12)/2 = 12/2 = 6
6. Из следующих пар событий совместными являются:
Варианты ответов:
1) А1 = {выход из строя телевизора работающего в гостиной}, В1 = {на кухне};
2) А2 = {попадание при одном выстреле}, В2 = {промах};
3) А3 = {хотя бы одно попадание при двух выстрелах}; В3 = {два попадания}.
4) А4 = {в магазин вошел покупатель старше 60 лет}; B4 = {в магазин вошла Елена Сергеевна};
5) А5 = {появление герба на первой монете}; В5 ={появление числа на второй монете}.
3)
3 Плотность вероятности f(x) равномерно распределенной случайной величины Х сохраняет на отрезке [3; 7] постоянное значение, равное h.; вне этого интервала плотность вероятности равна нулю. Найти h.
Варианты ответов:
1)1/3 2)1 3)1/2 4)1/4 5)2
f(x) = {0, x < 3
{h, 3 <= x <= 7
{0, x > 7
dx = 1 )
dx = \int\limits_{-\infty}^{3} f(x)dx + \int\limits_{3}^{7} f(x)dx + \int\limits_{7}^{+\infty} f(x)dx = )
 = 4h = 1 )
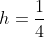
21. В группе 25 студентов, из которых отлично учится 5 человек, хорошо- 12, удовлетворительно- 6 и слабо-2. Преподаватель вызывает студента. Какова вероятность того, что вызванный студент или отличник или хорошист?
Варианты ответов:
1) 0,85 2) 8/25 3) 17/25 4) 0,5 5) 0,3
A = {студент отличник или хорошист}
A = B+C
B = {студент - отличник}
P(B) = 5/25
C = {студент - хорошист}
P(C) = 12/25
P(A) = P(B+C) = [события B и C несовместны] = P(B) + P(C) =
= 5/25 + 12/25 = 17/25
22. Из партии изделий товаровед отбирает изделия высшего сорта. Вероятность того, что наудачу взятое изделие, окажется высшего сорта равна 0,8. Найдите вероятность того, что из трех проверенных изделий только два высшего сорта.
Варианты ответов:
1)0,384 2)0,53)0,3 4) 0,4 5)0,616
n = 3 - количество изделий
p = 0.8 - изделие высшего сорта
q = 1 - p = 1 - 0.8 = 0.2
m - количество изделий высшего сорта
По формуле Бернулли
P(m=2) = C(2;3)*((0.8)^2)*(0.2) = 0.384
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 окт. 2009 10:31 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: vikycik написал 12 окт. 2009 1:50
23. Вероятность для компании, занимающейся строительством терминалов для аэропортов, получить контракт в стране А равна 0,4, вероятность выиграть его в стране В равна 0,3. Вероятность того, что контракты будут заключены и в стране А, и в стране В, равна 0,12. Чему равна вероятность того, что компания получит контракт хотя бы в одной стране?
Варианты ответов:
1)0,58 2)0,82 3)0,22 4)0,02 5)0,5
A = {контракт в стране A}
P(A) = 0.4
B = {контракт в стране B}
P(B) = 0.3
P(AB) = 0.12
P(A+B) = P(A) + P(B) - P(AB) = 0.4 + 0.3 - 0.12 = 0.58
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 окт. 2009 10:45 | IP
|
|
Nasto4ka

Новичок
|
    
Помогите решить пожалуйста.
Найти функцию распределения, дисперсию и среднее квадратичное отклонение: числа бракованных изделий среди 3-х взятых наугад, если вероятность изготовления бракованного изделия равна 0,1.
Мне бы только найти функцию распределения, а дальше я сама по формулам.
(Сообщение отредактировал Nasto4ka 12 окт. 2009 11:45)
|
Всего сообщений: 2 | Присоединился: октябрь 2009 | Отправлено: 12 окт. 2009 11:41 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Nasto4ka написал 12 окт. 2009 11:41
Найти функцию распределения, дисперсию и среднее квадратичное отклонение: числа бракованных изделий среди 3-х взятых наугад, если вероятность изготовления бракованного изделия равна 0,1.
Случайная величина X - число бракованных изделий среди трех. Данная случайная величина может принимать следующие значения: 0, 1, 2 или 3.
Событие {X=k} означает, что k изделий бракованные и 3-k изделий качественные (k=0,1,2,3).
n = 3 - количество изделий
p = 0.1 - вероятность того, что изделие бракованное
q = 1 - p = 1 - 0.1 = 0.9
Случайная величина X имеет распределение Бернулли с параметрами n = 3 и p = 0.1.
P(X=k) = C(k;3)*((0.1)^k)*((0.9)^(3-k)), k = 0,1,2,3
P(X=0) = (0.9)^3 = 0.729
P(X=1) = 3*(0.1)*(0.81) = 0.243
P(X=2) = 3*(0.01)*(0.9) = 0.027
P(X=3) = (0.1)^3 = 0.001
Ряд распределения случайной величины X имеет вид:
X 0 1 2 3
P 0.729 0.243 0.027 0.001
Функция распределения случайной величины X имеет вид:
F(x) = {0, x <= 0
{0.729, 0 < x <= 1
{0.972, 1 < x <= 2
{0.999, 2 < x <= 3
{1, x > 3
M(X) = np = 3*(0.1) = 0.3
D(X) = npq = 3*(0.1)*(0.9) = 0.27
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 окт. 2009 12:06 | IP
|
|
Nasto4ka

Новичок
|
    
Спасибо большое 
|
Всего сообщений: 2 | Присоединился: октябрь 2009 | Отправлено: 12 окт. 2009 12:35 | IP
|
|
asselka

Новичок
|
     
Помогите решить задачу, или может у кого есть ссылка на уже решенную:
Вероятность успешной сдачи первого экзамена для данного студента равна 0,9; второго экзамена - 0,8; третьего - 0,7; СВ Х - число сданных экзаменов. (Ответ должен быть таков М(Х)=2,4; D(X)=0,46)
Заранее спасибо тому, кто решит!
|
Всего сообщений: 16 | Присоединился: октябрь 2009 | Отправлено: 12 окт. 2009 12:57 | IP
|
|
Tatiyaaaaa


Новичок
|
    
Здравствуйте! Помогите пожалуйста решить 3 задачи!!! Слёзно-слещно умоляю(
1. Для проверки качества поступившей партии зерна по схеме собственно-случайной бесповторной выборки произведено 10%-ное обследование. В результате анализа установлено следующее распределение данных о влажности зерна:
Процент влажности /менее 8/8–10/10–12/12–14/14–16/16–
–18/18–20/Более 20/Итого
Число проб 7/15/30/35/25/18/7/3/140
Найти: а) вероятность того, что средний процент влажности зерна в партии отличается от ее среднего процента в выборке не более чем на 0,5% (по абсолютной величине); б) границы, в которых с вероятностью 0,95 заключена доля зерна, влажность которого менее 12%; в) объем выборки, при которой те же границы для доли зерна, полученные в пункте б), можно гарантировать с вероятностью 0,9876; дать ответ на тот же вопрос, если никаких предварительных данных о рассматриваемой доле нет.
2. По данным задачи 1, используя -критерий Пирсона, на уровне значимости a = 0,05 проверить гипотезу о том, что случайная величина X – процент влажности зерна – распределена по нормальному закону. Построить на одном чертеже гистограмму эмпирического распределения и соответствующую нормальную кривую.
3. Распределение 60 предприятий по затратам рабочего времени X (тыс. человеко-дней (чел. дн.)) и выпуску продукции Y (млн. руб.) представлены в таблице:
y 30–40 /40–50/50–60/60–70/70–80/Итого:
x
10–25 1 3 2 6
25–40 3 6 4 1 14
40–55 3 7 6 1 17
55–70 1 6 4 4 15
70–85 2 5 1 8
Итого: 4 13 21 16 6 60
Необходимо:
1) Вычислить групповые средние , построить эмпирические линии регрессии;
2) Предполагая, что между переменными X и Y существует линейная корреляционная зависимость: а) найти уравнения прямых регрессии, построить их графики на одном чертеже с эмпирическими линиями регрессии и дать экономическую интерпретацию полученных уравнений; б) вычислить коэффициент корреляции; на уровне значимости  = 0,05 оценить его значимость и сделать вывод о тесноте и направлении связи между переменными X и Y; в) используя соответствующее уравнение регрессии, оценить средний выпуск продукции предприятия с затратами рабочего времени 55 тыс. чел. дн.
|
Всего сообщений: 4 | Присоединился: октябрь 2009 | Отправлено: 12 окт. 2009 13:27 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: asselka написал 12 окт. 2009 12:57
Вероятность успешной сдачи первого экзамена для данного студента равна 0,9; второго экзамена - 0,8; третьего - 0,7; СВ Х - число сданных экзаменов. (Ответ должен быть таков М(Х)=2,4; D(X)=0,46)
Случайная величина X - число сданных экзаменов. Данная случайная величина может принимать следующие значения:
{X=0} - никто не сдал экзамен
{X=1} - один студент сдал экзамен
{X=2} - два студента сдали экзамен
{X=3} - все сдали экзамен
P(X=0) = (1-0.9)*(1-0.8)*(1-0.7) = (0.1)*(0.2)*(0.3) = 0.006
P(X=1) = (0.9)*(1-0.8)*(1-0.7) + (1-0.9)*(0.8)*(1-0.7) +
+ (1-0.9)*(1-0.8)*(0.7) =
= (0.9)*(0.2)*(0.3) + (0.1)*(0.8)*(0.3) + (0.1)*(0.2)*(0.7) =
= 0.054 + 0.024 + 0.014 = 0.092
P(X=2) = (0.9)*(0.8)*(1-0.7) + (0.9)*(1-0.8)*(0.7) +
+ (1-0.9)*(0.8)*(0.7) =
= (0.9)*(0.8)*(0.3) + (0.9)*(0.2)*(0.7) + (0.1)*(0.8)*(0.7) =
= 0.216 + 0.126 + 0.056 = 0.398
P(X=3) = (0.9)*(0.8)*(0.7) = 0.504
Ряд распределения случайной величины X имеет вид:
X 0 1 2 3
P 0.006 0.092 0.398 0.504
M(X) = 0*(0.006) + 1*(0.092) + 2*(0.398) + 3*(0.504) =
= 0.092 + 0.796 + 1.512 = 2.4
M(X^2) = 0*(0.006) + 1*(0.092) + 4*(0.398) + 9*(0.504) =
= 0.092 + 1.592 + 4.536 = 6.22
D(X) = M(X^2) - (M(X))^2 = 6.22 - 5.76 = 0.46
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 окт. 2009 13:57 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности