Alessia
Новичок
|
    
Помогите пожалуйста в решении задачки,если Вам не составит труда! Теория вероятностей только началась, я пока что тыквва бестолковая )
1)Симметричная игральная кость подбрасывается трижды.
Событие А:При первом бросании выпало 2 очка
Событие В:Сумма выпавших очков равна 9
Событие С: Результаты бросаний отличаются не менее чем на 1
Найти вероятность событий А,В,С
2)В компьютерном классе5 компьютеров, из которых 2 с принтерами. 3 студентов,придя на лабораторный практикум,случайным образом рассаживаются за компьютерами. Найти вероятность событий:
А= будет занято 3 компьютера с принтерами (это получается невозможное событие кажется, т.к принтера 2?)
В=Будет занято не более 2 компьютеров с принтерами
С=будет занят по крайней мере один компьютер с принтером и один без принтера;
3)На занятия в институт студент Х всегда ездит автобусами двух маршрутов с пересадкой. Интервал движения автобусов равен 10 мин,найти вероятность событий:
А=суммарное время ожидания автобусов на обеих остановках будет не более 15 мин
В= максимальное из двух времени ожиданий на остановках составит не более 5 мин
С=разность во времени ожидания автобуса на 1-й и 2-й остановках будет не более 3 минут;
Очень благадарна тем, кто откликнется,Вы будите моим спасителем))
(Сообщение отредактировал Alessia 11 окт. 2009 22:43)
(Сообщение отредактировал Alessia 11 окт. 2009 23:23)
|
Всего сообщений: 8 | Присоединился: октябрь 2009 | Отправлено: 11 окт. 2009 19:32 | IP
|
|
RKI 
Долгожитель
|
Цитата: Vasilisa1 написал 11 окт. 2009 15:33
я просто не представляю, откуда брать эти В и С.
или это опечатка? или я что-то недопонимаю?
А, если х<0
F(x)=В+С*сos (3x), если 0<=х<=PI/3
D, если х> PI/3
F(x) = {A, x < 0
{B + C(cos3x), 0 <= x <= П/3
{D, x > П/3
 = 0 )
 = \lim\limits_{x \to -\infty} A = A = 0 )
F(x) = {0, x < 0
{B + C(cos3x), 0 <= x <= П/3
{D, x > П/3
 = F(0) )
 = \lim\limits_{x \to -0} 0 = 0 )
 = B + C(cos0) = B + C )
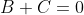
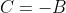
F(x) = {0, x < 0
{B - B(cos3x), 0 <= x <= П/3
{D, x > П/3
 = 1 )
 = \lim\limits_{x \to +\infty} D = D = 1 )
F(x) = {0, x < 0
{B - B(cos3x), 0 <= x <= П/3
{1, x > П/3
 = F(\frac{\pi}{3}) )
 = \lim\limits_{x \to \frac{\pi}{3}+0} 1 = 1 )
 = B - Bcos \pi = B + B = 2B )
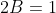
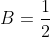
F(x) = {0, x < 0
{(1/2)(1 - cos3x), 0 <= x <= П/3
{1, x > П/3
f(x) = F'(x)
f(x) = {0, x < 0
{(3/2)sin3x, 0 <= x <= П/3
{0, x > П/3
 = \int\limits_{-\infty}^{+\infty} xf(x)dx = \int\limits_{-\infty}^{0} xf(x)dx + \int\limits_{0}^{\frac{\pi}{3} } xf(x)dx + \int\limits_{\frac{\pi}{3} }^{+\infty} xf(x)dx = )
dx + \int\limits_{\frac{\pi}{3} }^{+\infty} 0dx = 0 + \frac{3}{2}\int\limits_{0}^{\frac{\pi}{3} } x(sin3x)dx + 0 = )
dx = - \frac{1}{2} \int\limits_{0}^{\frac{\pi}{3} } xd(cos3x) = )
 |_{0}^{\frac{\pi}{3} } + \frac{1}{2} \int\limits_{0}^{\frac{\pi}{3} } (cos3x)dx = \frac{\pi}{6} + \frac{1}{6} (sin3x) |_{0}^{\frac{\pi}{3} } = \frac{\pi}{6} )
 = \frac{\pi}{6} )
 = \int\limits_{-\infty}^{+\infty} x^2 f(x)dx = \int\limits_{-\infty}^{0} x^2 f(x)dx + \int\limits_{0}^{\frac{\pi}{3} } x^2 f(x)dx + \int\limits_{\frac{\pi}{3} }^{+\infty} x^2 f(x)dx = )
dx + \int\limits_{\frac{\pi}{3} }^{+\infty} 0dx = 0 + \frac{3}{2}\int\limits_{0}^{\frac{\pi}{3} } x^2 (sin3x)dx + 0 = )
dx = - \frac{1}{2} \int\limits_{0}^{\frac{\pi}{3} } x^2 d(cos3x) = )
 |_{0}^{\frac{\pi}{3} } + \frac{1}{2} \int\limits_{0}^{\frac{\pi}{3} } (cos3x)d(x^2) = \frac{\pi^2}{18} + \int\limits_{0}^{\frac{\pi}{3} } x(cos3x)dx = )
 = )
 |_{0}^{\frac{\pi}{3} } - \frac{1}{3} \int\limits_{0}^{\frac{\pi}{3} } (sin3x)dx = )
 |_{0}^{\frac{\pi}{3} } = \frac{\pi^2}{18} - \frac{1}{9} - \frac{1}{9} = \frac{\pi^2}{18} - \frac{2}{9} )
 = M(X^2) - M^2 (X) = \frac{\pi^2}{18} - \frac{2}{9} - \frac{\pi^2}{36} = \frac{\pi^2}{36} - \frac{2}{9} )
 = \frac{\pi^2 - 8}{36} )
(Сообщение отредактировал RKI 11 окт. 2009 20:14)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 окт. 2009 19:43 | IP
|
|
Vasilisa1
Новичок
|
спасибо огромное. очень сильно помогли.
|
Всего сообщений: 24 | Присоединился: май 2009 | Отправлено: 11 окт. 2009 20:12 | IP
|
|
RKI
Долгожитель
|
Цитата: Kcunka написал 11 окт. 2009 17:56
3)Случайная величина Х равна числу появлений «герба» в серии из 8 бросаний монеты. Найти закон распределения и функцию распределения F(x) этой случайной величины; вычислить ее математическое ожидание MX и дисперсию DX; построить график F(x).
Случайная величина X - число выпадений герба в серии из 8 бросаний. Данная случайная величина может принимать значения от 0 до 8.
Событие {X=k} означает, что k раз выпал герб и 8-kраз выпала решка (k=0,1,2,...,8).
n = 8 - количество бросаний
p = 1/2 - вероятность выпадения герба при одном бросании
q = 1 - p = 1 - 1/2 = 1/2
Случайная величина X имеет распределение Бернулли с параметрами n=8 и p = 1/2
P(X=k) = C(k;8)*((1/2)^k)*((1/2)^(8-k)) = C(k;8)/256
k = 0,1,2,...,8
Ряд распределения случайной величины X имеет вид:
X 0 1 2 3 4 5
P 1/256 8/256 28/256 56/256 70/256 56/256
X 6 7 8
P 28/256 8/256 1/256
Функция распределения случайной величины X имеет вид:
F(x) = {0, x <= 0
{1/256, 0 < x <= 1
{9/256, 1 < x <= 2
{37/256, 2 < x <= 3
{93/256, 3 < x <= 4
{163/256, 4 < x <= 5
{219/256, 5 < x <= 6
{247/256, 6 < x <= 7
{255/256, 7 < x <= 8
{1, x > 8
Для случайной величины X, имеющей распределение Бернулли с параметрами n и p,
M(X) = np
D(X) = npq
M(X) = 8*(1/2) = 4
D(X) = npq = 8*(1/2)*(1/2) = 2
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 окт. 2009 20:53 | IP
|
|
chandler
Новичок
|
Ha от
(Сообщение отредактировал chandler 26 окт. 2009 21:18)
|
Всего сообщений: 43 | Присоединился: апрель 2009 | Отправлено: 11 окт. 2009 21:27 | IP
|
|
RKI
Долгожитель
|
Цитата: chandler написал 11 окт. 2009 21:27
Ha отдельных карточках написаны цифры 1,2,3,4,5,6,7,8,9. Все девять карточек тщательно перемешаны, после чего наугад вынимают четыре из них и раскладывают в ряд друг за другом. Какова вероятность получить при этом : а)четное число
у меня получается
n = A(9,4) = 3024
m = 4! = 24
P(A) = 24/3024
Посчитаем число n всевозможных исходов. Способов достать 4 карточки из 9 имеющихся (порядок важен):
n = A(4;9) = 9!/5! = 6*7*8*9 = 3024
A = {четное число}
Посчитаем число m исходов, благоприятных событию A. На последнем месте может стоять любая из следующих цифр: 2, 4, 6 или 8, то есть m1 = 4 возможности (тогда число гарантированно будет четным). Зафиксировали последнюю цифру. Остались еще восемь свободных цифр и три первых позиции числа. Способов выбрать 3 цифры из 8 имеющихся (порядок важен):
m2 = A(3;8) = 8!/5! = 6*7*8 = 336
По правилу произведения m = m1*m2 = 4*336 = 1344
По классическому определению вероятности
P(A) = m/n = 1344/3024 = 4/9
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 окт. 2009 23:42 | IP
|
|
RKI
Долгожитель
|
Цитата: chandler написал 11 окт. 2009 21:27
Вероятности того, что при одном выстреле из орудия получаются недолет,
попадание и перелет, равны 0.1; 0.7; 0.2. Для другого орудия вероятности
этих событие равны соответственно 0.2; 0.65; 0.15. Наугад выбранное
орудие стреляет трижды. Отмечены; одно попадание, один недолет и один
перелет. Найти вероятность того, что стреляло первое орудие.
А почему тут присутствует множитель 6? в Р(А/Н) ?
Множитель 6 присутствует по следующей причине.
Учитываются следующие возможности
{недолет, попадание, перелет}
{недолет, перелет, попадание}
{попадание, недолет, перелет}
{попадание, перелет, недолет}
{перелет, недолет, попадание}
{перелет, попадание, недолет}
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 окт. 2009 23:45 | IP
|
|
RKI
Долгожитель
|
Цитата: ZLOYALEX123 написал 11 окт. 2009 13:29
Задача 7
Определить закон распределения дискретной случайной величины , если известна ее дисперсия, причем x1<x2<x3<x4. Определить M(X)
x1=x1 x2=0 x3= 3 x4=6 p1= 0.6 p2=p2 p3=0.1 p4=0.1 D(X)= 9.09
X x1 0 3 6
P 0.6 p2 0.1 0.1
0.6 + p2 + 0.1 + 0.1 = 1
0.8 + p2 = 1
p2 = 0.2
X x1 0 3 6
P 0.6 0.2 0.1 0.1
M(X) = (0.6)x1 + (0.2)*0 + (0.1)*3 + (0.1)*6 =
= (0.6)x1 + 0 + 0.3 + 0.6 = (0.6)x1 + 0.9
M(X^2) = (0.6)(x1)^2 + (0.2)*0 + (0.1)*9 + (0.1)*36 =
= (0.6)(x1)^2 + 0 + 0.9 + 3.6 = (0.6)(x1)^2 + 4.5
D(X) = M(X^2) - (M(X))^2 =
= (0.6)(x1)^2 + 4.5 - ((0.6)x1 + 0.9)^2 =
= (0.6)(x1)^2 + 4.5 - (0.36)(x1)^2 - (1.08)x1 - 0.81 =
= (0.24)(x1)^2 - (1.08)x1 + 3.69 = 9.09
(0.24)(x1)^2 - (1.08)x1 - 5.4 = 0
(0.04)(x1)^2 - (0.18)x1 - 0.9 = 0
x1 = - 3 или x1 = 7.5
x1 < x2 < x3 < x4 => x1 = - 3
X -3 0 3 6
P 0.6 0.2 0.1 0.1
M(X) = (0.6)x1 + 0.9 = (0.6)*(-3) + 0.9 = - 0.9
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 11 окт. 2009 23:57 | IP
|
|
RKI
Долгожитель
|
Цитата: ZLOYALEX123 написал 11 окт. 2009 13:29
Задание 8
Случайная величина Х задана интегральной функцией распределения F(x). Определить :
1. Дифференциальную функцию f(x)
2.математическое ожидание и дисперсию случайной велечины
3.построить графики функций f(x) и F(x)
F(x)= система 0 , если x<4
0.5x -2 , если 4<=x<=6
1, если x>6
F(x) = {0, x < 4
{(0.5)x - 2, 4 <= x <= 6
{1, x > 6
f(x) = F'(x)
f(x) = {0, x < 4
{0.5, 4 < x < 6
{0, x > 6
 = \int\limits_{-\infty}^{+\infty} xf(x)dx = \int\limits_{-\infty}^{4} xf(x)dx + \int\limits_{4}^{6} xf(x)dx + \int\limits_{6}^{+\infty} xf(x)dx = )
xdx + \int\limits_{6}^{+\infty} 0dx = 0 + (0.25)x^2 |_{4}^{6} + 0 = )
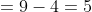
 = 5 )
 = \int\limits_{-\infty}^{+\infty} x^2 f(x)dx = \int\limits_{-\infty}^{4} x^2 f(x)dx + \int\limits_{4}^{6} x^2 f(x)dx + \int\limits_{6}^{+\infty} x^2 f(x)dx = )
x^2 dx + \int\limits_{6}^{+\infty} 0dx = 0 + \frac{(0.5)x^3}{3} |_{4}^{6} + 0 = )
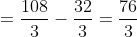
 = \frac{76}{3} )
 = M(X^2) - M^2 (X) = \frac{76}{3} - 25 = \frac{1}{3} )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 окт. 2009 0:06 | IP
|
|
RKI
Долгожитель
|
Цитата: ZLOYALEX123 написал 11 окт. 2009 13:29
Задача9
Определить вероятность того, что нормально распределенная случайная величина Х принимает значение . находящиеся в интервале (альфа, бета). Если математическое ожидание величины равно a, а среднее квадратическое отклонение – сигма
а= 20 сигма=5 альфа=10 бета=14
 = \Phi (\frac{14-20}{5}) - \Phi (\frac{10-20}{5}) = \Phi (-1.2) - \Phi (-2) = )
 + \Phi (2) \sim - 0.3849 + 0.4772 = 0.0923 )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 12 окт. 2009 0:10 | IP
|
|
|
Форум
Решение задач по теории вероятности
