Delonge
Новичок
|
   
Спасибо огромное...восхищена вашим умом...дай Бог вам здоровья..
|
Всего сообщений: 4 | Присоединился: сентябрь 2009 | Отправлено: 28 сен. 2009 22:00 | IP
|
|
tatbel
Новичок
|
пожайлуста помогите решить контрольную!
1для поражения цели достаточно одного попадания.По цели произведено три выстрела с вероятностью попадания 0,75;0,85 и 0,90 соответственно.Найти вероятность того, что цель будет поражена.
2.В ящике находятся 15 деталей, пять из которых бракованные.Наудачу отобраны три детали.Какова вероятность, что все они окажутся бракованными?
Очень благодарна за помощь!!
|
Всего сообщений: 2 | Присоединился: сентябрь 2009 | Отправлено: 29 сен. 2009 9:42 | IP
|
|
RKI 
Долгожитель
|
Цитата: vikycik написал 28 сен. 2009 20:09
RKI помните вы решали задачу: Из урны, содержащей 2 белых и 3 черных шара, последовательно вытаскивают по 2 шара (каждый раз возвращая их обратно) до появления двух шаров одного цвета. Составь закон распределения для числа вытаскивания шаров. Найдите математическое ожидание данной величины.
Там получилось Математическое ожидание случайной величины X, распределенной по геометрическому закону, равно
M(X) = 1/p = 1/(0.4) = 2.5
Откуда такая формула вычисления M(X) = 1/p?
Для многих известных распределений формула для нахождения математического ожидания и дисперсии известны.
В том числе они известны и для геометрического распределения
Вывод формулы можно посмотреть здесь:
Теория вероятностей в примерах
http://exir.ru/cgi-bin/ikonboard/topic.cgi?forum=7&topic=2182&start=460
ПРИМЕР 449
http://exir.ru/cgi-bin/ikonboard/topic.cgi?forum=7&topic=2182&start=80
ПРИМЕР 81
(Сообщение отредактировал RKI 29 сен. 2009 11:04)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 29 сен. 2009 10:56 | IP
|
|
RKI
Долгожитель
|
Цитата: tatbel написал 29 сен. 2009 9:42
1для поражения цели достаточно одного попадания.По цели произведено три выстрела с вероятностью попадания 0,75;0,85 и 0,90 соответственно.Найти вероятность того, что цель будет поражена.
Ai = {попадание при i-том выстреле}
i = 1, 2, 3
P(A1) = 0.75
P(A2) = 0.85
P(A3) = 0.9
не Ai = {промах при i-том выстреле}
i = 1,2,3
P(не A1) = 1 - P(A1) = 1 - 0.75 = 0.25
P(не A2) = 1 - P(A2) = 1 - 0.85 = 0.15
P(не A3) = 1 - P(A3) = 1 - 0.9 = 0.1
A = {цель поражена}
не A = {цель не поражена}
не A = (не A1)(не A2)(не A3)
P(не A) = P((не A1)(не A2)(не A3)) =
= [события не A1, не A2 и не A3 являются независимыми] =
= P(не A1)*P(не A2)*P(не A3) =
= (0.25)*(0.15)*(0.1) = 0.00375
P(A) = 1 - P(не A) = 1 - 0.00375 = 0.99625
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 29 сен. 2009 11:09 | IP
|
|
RKI
Долгожитель
|
Цитата: tatbel написал 29 сен. 2009 9:42
2.В ящике находятся 15 деталей, пять из которых бракованные.Наудачу отобраны три детали.Какова вероятность, что все они окажутся бракованными?
A = {три детали бракованные}
Посчитаем число n всевозможных исходов. Способов отобрать 3 детали из имеющихся 15:
n = C(3;15) = 15!/3!12! = (13*14*15)/(1*2*3) = 455
Посчитаем число m исходов, благоприятхных событию A. Способов отобрать 3 бракованные детали из имеющихся 5 бракованных:
m = C(3;5) = 5!/3!2! = (4*5)/(1*2) = 10
По классическому определению вероятности
P(A) = m/n = 10/455 = 2/91
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 29 сен. 2009 11:14 | IP
|
|
RKI
Долгожитель
|
Цитата: Kcunka написал 28 сен. 2009 22:00
.Каждый избиратель независимо от остальных избирателей, отдаёт свой голос за кандидата А с вероятностью 0,1(2+5) и за кандидата В – с веро-ятностью 1-0,1(2+5). Оценить вероятность того, что в результате голо-сования на избирательном участке (5000 избирателей) один из кандида-тов опередит другого:
а) ровно на 1900 голосов
б) не менее, чем на 1900 голосов
n = 5000 - количество избирателей
Пусть случайная величина X - число избирателей, отдавших свой голос за кандидата A.
p = 0.7 - вероятность того, что один отдельно вязтый избиратель отдал свой голос за кандидата A
q = 0.3
np = 5000*(0.7) = 3500
npq = 5000*(0.7)*(0.3) = 1050
Если за кандидата A было отдано X голосов, то за кандидата B - 5000-X.
а)
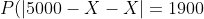 = P(|5000-2X| = 1900) = )
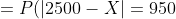 = P(2500 - X = 950) + P(2500 - X = - 950) = )
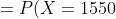 + P(X = 3450) \sim )
 + \frac{1}{\sqrt{1050} }\phi (\frac{3450 - 3500}{\sqrt{1050} }) \sim )
 + \frac{1}{\sqrt{1050} }\phi (-1.54) = )
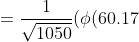 + \phi (1.54)) \sim \frac{1}{\sqrt{1050} } (0 + 0.12188) \sim 0.003761298... )
б)
 = P(|5000-2X| \ge 1900) = )
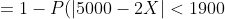 = 1 - P(- 1900 < 5000 - 2X < 1900) = )
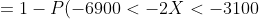 = 1 - P(1550 < X < 3450) = )
 - \Phi(\frac{1550-3500}{\sqrt{1050} }) \right) \sim )
 + \Phi (- 60.17) = 1 + \Phi (1.54) - \Phi (60.17) \sim )
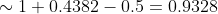
(Сообщение отредактировал RKI 29 сен. 2009 12:00)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 29 сен. 2009 11:40 | IP
|
|
can kill
Новичок
|
Из пяти гвоздик две белые. Составить закон распределения и найти функцию распределения случайной величины, выражающей число белых гвоздик среди двух одновременно взятых.
|
Всего сообщений: 4 | Присоединился: сентябрь 2009 | Отправлено: 29 сен. 2009 12:19 | IP
|
|
Kcunka
Новичок
|
Большое спасибо RKI за помощь!! только у меня один вопрос: а что означает буква Ф?
|
Всего сообщений: 6 | Присоединился: сентябрь 2009 | Отправлено: 29 сен. 2009 12:42 | IP
|
|
RKI
Долгожитель
|
Цитата: Kcunka написал 29 сен. 2009 12:42
Большое спасибо RKI за помощь!! только у меня один вопрос: а что означает буква Ф?
Означает функцию Лапласа Ф
(Сообщение отредактировал RKI 29 сен. 2009 12:57)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 29 сен. 2009 12:57 | IP
|
|
RKI
Долгожитель
|
Цитата: can kill написал 29 сен. 2009 12:19
Из пяти гвоздик две белые. Составить закон распределения и найти функцию распределения случайной величины, выражающей число белых гвоздик среди двух одновременно взятых.
Случайная величина X - число белых гвоздик из 2 взятых. Данная случайная величина может принимать следующие значения:
{X=0} - две гвоздики другого цвета
{X=1} - одна гваздика белого цвета и одна гвоздика другого цвета
{X=2} - две гвоздики белого цвета
P(X=0) = C(2;3)/C(2;5) = 3/10 = 0.3
P(X=1) = C(1;3)C(1;2)/C(2;5) = 6/10 = 0.6
P(X=2) = C(2;2)/C(2;5) = 1/10 = 0.1
Закон распределения случайной величины X имеет вид:
X 0 1 2
P 0.3 0.6 0.1
Функция распределения случайной величины X имеет вид:
F(x) = {0, x <= 0
{0.3, 0 < x <= 1
{0.9, 1 < x <= 2
{1, x > 2
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 29 сен. 2009 13:02 | IP
|
|
Форум
Решение задач по теории вероятности
