Delonge

Новичок
|
    
Огромное спасибо!Прошлую задачу засчитали и все благодаря вам! но задали еще одну...
Среди преступлений 10 % составляют
убийства, 25% – кражи. Раскрывают 2 из каж-
дых 3 убийств, 3 из каждых 5 краж и каждое
второе преступление других видов. Определи-
те вероятность того, что нераскрытое пре-
ступление – кража.
Помогите...обратиться больше некуда..простите за доставленное беспокойство..
|
Всего сообщений: 4 | Присоединился: сентябрь 2009 | Отправлено: 27 сен. 2009 22:13 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Delonge написал 27 сен. 2009 22:13
Среди преступлений 10 % составляют
убийства, 25% – кражи. Раскрывают 2 из каж-
дых 3 убийств, 3 из каждых 5 краж и каждое
второе преступление других видов. Определи-
те вероятность того, что нераскрытое пре-
ступление – кража.
H1 = {преступление - убийство}
H2 = {преступление - кража}
H3 = {преступление другого вида}
P(H1) = 0.1
P(H2) = 0.25
P(H3) = 1 - P(H1) - P(H2) = 1 - 0.1 - 0.25 = 0.65
A = {преступление не раскрыто}
не A = {преступление раскрыто}
не A|H1 = {преступление раскрыто при условии, что это убийство}
не A|H2 = {преступление раскрыто при условии, что это кража}
не A|H3 = {преступление раскрыто при условии, что это преступление другого вида}
P(не A|H1) = 2/3
P(не A|H2) = 3/5
P(не A|H3) = 1/2
P(A|H1) = 1 - P(не A|H1) = 1 - 2/3 = 1/3
P(A|H2) = 1 - P(не A|H2) = 1 - 3/5 = 2/5
P(A|H3) = 1 - P(не A|H3) = 1 - 1/2 = 1/2
По формуле полной вероятности
P(A) = P(H1)P(A|H1) + P(H2)P(A|H2) + P(H3)P(A|H3) =
= (0.1)*(1/3) + (0.25)*(2/5) + (0.65)*(1/2) =
= (0.1)/3 + 0.1 + 0.325 = (0.1 + 0.3 + 0.975)/3 =
= (1.375)/3
По формуле Байеса
P(H2|A) = P(H2)P(A|H2)/P(A) = (0.25)*(2/5)/(1.375)/3 =
= (0.1)/(1.375)/3 = (0.3)/(1.375) = 300/1375 = 12/55
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 28 сен. 2009 10:56 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: vikycik написал 27 сен. 2009 16:50
1.Плотность вероятности случайной величины Х задана формулой
g(x)= система: 0, при х<0
C(e^-x)2x,при х>=0
Найти: а) постоянную С; б) вероятность, что величина Х примет значение из интервала (0; 1).
g(x) = {0, x < 0
{2Cx(e^(-x)), x >= 0
а) dx = 1 )
dx = \int\limits_{-\infty}^{0} g(x)dx + \int\limits_{0}^{+\infty} g(x)dx = )
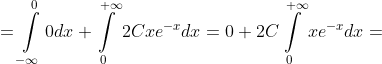
 = - 2Cx e^{-x} |_{0}^{+\infty} + 2C\int\limits_{0}^{+\infty} e^{-x} dx = )
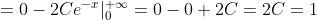

g(x) = {0, x < 0
{x(e^(-x)), x >= 0
б)  = \int\limits_{0}^{1} g(x)dx = \int\limits_{0}^{1} x e^{-x} dx = )
 = - x e^{-x} |_{0}^{1} + \int\limits_{0}^{1} e^{-x} dx = )
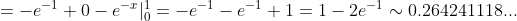
(Сообщение отредактировал RKI 28 сен. 2009 11:14)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 28 сен. 2009 11:06 | IP
|
|
Omni

Новичок
|
    
Помогите, пож-та, решить:
Было посажено 500 кустарников, вероятность прижиться каждому из которых равна 0,8. Оценить вероятность того, что приживутся от 100 до 440 кустарников (включительно). Вычислить вероятность того же события, используя следствие из интегральной теоремы Муавра-Лапласа. Пояснить различие результатов.
Во втором номере я начала так:
Случайная величина X имеет биномиальный закон распределения. Поэтому a=M(X)=500*0.8=400, D(X)=500*0.8*0.2=80.
По интегральной теореме Муавра-Лапласа.
P(100≤X≤440)=1/2 [Φ((440-400)/√80)-Φ((100-400)/√80) ]=1/2 [Φ(4.4721360)-Φ(-33.5410197) ]= ..а вот дальше не могу понять как делать, потому что получается странный результат...
И как найти вероятность другим путем и сравнить результаты?
|
Всего сообщений: 7 | Присоединился: сентябрь 2009 | Отправлено: 28 сен. 2009 11:20 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: vikycik написал 27 сен. 2009 16:50
2.Случайная величина Х имеет плотность вероятности
g(x)= cистема: 0,при |х|>=П/2
cos x/2,при |х|<П/2
Найти интегральную функцию распределения, математическое ожидание и дисперсию.
g(x) = {0, x <= -П/2
{(1/2)cosx, -П/2 < x < П/2
{0, x >= П/2
1) интегральная функция распределения
 = \int\limits_{-\infty}^{x} g(t)dt )
Если 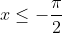 , то , то
 = \int\limits_{-\infty}^{x} g(t)dt = \int\limits_{-\infty}^{x} 0dt = 0. )
Если 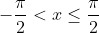 , то , то
 = \int\limits_{-\infty}^{x} g(t)dt = \int\limits_{-\infty}^{-\frac{\pi}{2} } g(t)dt + \int\limits_{-\frac{\pi}{2} }^{x} g(t)dt = )
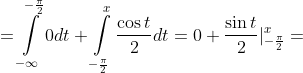
 )
Если  , то , то
 = \int\limits_{-\infty}^{x} g(t)dt = \int\limits_{-\infty}^{-\frac{\pi}{2} } g(t)dt + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } g(t)dt + \int\limits_{\frac{\pi}{2} }^{x} g(t)dt = )
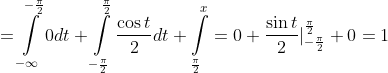
F(x) = {0, x <= - П/2
{(1/2)(sinx + 1), - П/2 < x <= П/2
{1, x > П/2
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 28 сен. 2009 11:28 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: vikycik написал 27 сен. 2009 16:50
2.Случайная величина Х имеет плотность вероятности
g(x)= cистема: 0,при |х|>=П/2
cos x/2,при |х|<П/2
Найти интегральную функцию распределения, математическое ожидание и дисперсию.
g(x) = {0, x <= -П/2
{(1/2)cosx, -П/2 < x < П/2
{0, x >= П/2
2) математическое ожидание
 = \int\limits_{-\infty}^{+\infty} xg(x)dx = \int\limits_{-\infty}^{-\frac{\pi}{2} } xg(x)dx + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } xg(x)dx + \int\limits_{\frac{\pi}{2} }^{+\infty} xg(x)dx = )

 = \frac{1}{2}x\sin{x} |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } - \frac{1}{2} \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } \sin{x}dx = )
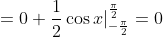
 = 0 )
(Сообщение отредактировал RKI 28 сен. 2009 11:39)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 28 сен. 2009 11:37 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: vikycik написал 27 сен. 2009 16:50
2.Случайная величина Х имеет плотность вероятности
g(x)= cистема: 0,при |х|>=П/2
cos x/2,при |х|<П/2
Найти интегральную функцию распределения, математическое ожидание и дисперсию.
3) дисперсия
g(x) = {0, x <= -П/2
{(1/2)cosx, -П/2 < x < П/2
{0, x >= П/2
 = \int\limits_{-\infty}^{+\infty} x^{2} g(x)dx = )
dx + \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } x^{2} g(x)dx + \int\limits_{\frac{\pi}{2} }^{+\infty} x^{2} g(x)dx = )
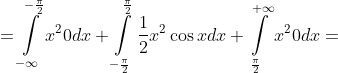
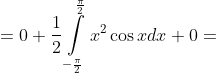
 = \frac{1}{2}x^{2}\sin{x} |_{-\frac{\pi}{2} }^{\frac{\pi}{2} } - \frac{1}{2} \int\limits_{-\frac{\pi}{2} }^{\frac{\pi}{2} } \sin{x}d(x^{2}) = )
 = )
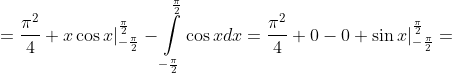
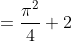
 = \frac{\pi^{2} }{4} + 2 )
 = M(X^2) - M^{2}(X) = \frac{\pi^{2} }{4} + 2 - 0 = \frac{\pi^{2} }{4} + 2)
(Сообщение отредактировал RKI 28 сен. 2009 11:50)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 28 сен. 2009 11:48 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: vikycik написал 27 сен. 2009 16:50
3.Найти плотность вероятности случайной величины Х, которая имеет функцию распределения:
F(x)=система: 0, при х<=0
1/П (х-1/2 sin 2x), при 0<x<П
1, при х>=П
F(x) = {0, x <= 0
{(1/П)(x - (1/2)sin2x), 0 < x < П
{1, x >= П
g(x) = F'(x)
g(x) = {0, x <= 0
{(1/П)(1 - cos2x), 0 < x < П
{0, x >= П
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 28 сен. 2009 11:53 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Omni написал 28 сен. 2009 11:20
Было посажено 500 кустарников, вероятность прижиться каждому из которых равна 0,8. Оценить вероятность того, что приживутся от 100 до 440 кустарников (включительно). Вычислить вероятность того же события, используя следствие из интегральной теоремы Муавра-Лапласа. Пояснить различие результатов.
Пусть случайная величина X - число прижившихся кустарников из заданных 500.
n = 500 - общее количество кустарников
p = 0.8 - вероятность прижиться для одного отдельно взятого кустарника
q = 1 - p = 1 - 0.8 = 0.2
Случайная величина X имеет распределение Бернулии. Следовательно,
M(X) = np = 500*(0.8) = 400
D(X) = npq = 500*(0.8)*(0.2) = 80
P(100 <= X <= 440) > P(360 <= X <= 440) = [взяли в рассмотрение меньший диапазон кустаников (не от 100 до 440, а от 360 до 440), поэтому исходная вероятность умеьшилась] =
= P(360 - M(X) <= X - M(X) <= 440 - M(X)) =
= P(360 - 400 <= X - M(X) <= 440 - 400) =
= P(-40 <= X - M(X) <= 40) = P(|X - M(X)| <= 40) >
> [по неравенству Чебышева] > 1 - D(X)/1600 = 1 - 80/1600 =
= 1 - 0.05 = 0.95
Таким образом, используя неравенство Чебышева, была получена оценка
P(100 <= X <= 440) > 0,95
По интегральной формуле Муавра - Лапласа
P(100 <= X <= 440) ~
~ Ф((440-400)/sqrt(80)) - Ф((100-400)/sqrt(80)) ~
~ Ф(4.47) - Ф(- 33.54) ~ Ф(4.47) + Ф(33.54) ~
~ 0.499997 + 0.5 ~ 0.99997
Интегральная формула Муавра-Лапласа дает более точный результат
(Сообщение отредактировал RKI 28 сен. 2009 12:26)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 28 сен. 2009 12:09 | IP
|
|
Omni

Новичок
|
    
Спасибо, RKI !
Понятно, по неравенству Чебышева > 0,95. а по Муавру-Лапласу. я правильно стала вычислять :
P(100≤X≤440)=1/2 [Φ((440-400)/√80)-Φ((100-400)/√80) ]=1/2 [Φ(4.4721360)-Φ(-33.5410197) ] ? я только не пойму как мне вычислить окончательный результат? какие-то странные числа получились...
объясните, пожалуйста, ....
|
Всего сообщений: 7 | Присоединился: сентябрь 2009 | Отправлено: 28 сен. 2009 12:23 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности

 Форум
Форум

 Математика
Математика

 Решение задач по теории вероятности
Решение задач по теории вероятности