bz9I
Новичок
|
    
Добрый вечер не могли б помочь мне решить этот примерчик
(x^3)*y'+(x^2)*y+1=0
|
Всего сообщений: 2 | Присоединился: ноябрь 2007 | Отправлено: 28 нояб. 2007 18:15 | IP
|
|
Trushkov
Долгожитель
|
 
Цитата: bz9I написал 28 нояб. 2007 18:15
Добрый вечер не могли б помочь мне решить этот примерчик
(x^3)*y'+(x^2)*y+1=0
Сначала рассматриваете уравнения с нулевой правой частью: x^3*y'+x^2*y=0, а потом варьируете произвольную постоянную
|
Всего сообщений: 273 | Присоединился: январь 2006 | Отправлено: 28 нояб. 2007 18:30 | IP
|
|
bz9I
Новичок
|
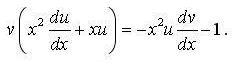
я путаюсь такими видами преобразований
в моем случае вместо x^2 =x^3 x=x^2
(Сообщение отредактировал bz9I 28 нояб. 2007 19:44)
|
Всего сообщений: 2 | Присоединился: ноябрь 2007 | Отправлено: 28 нояб. 2007 19:42 | IP
|
|
Psyland
Новичок
|
Умные люди помогите пожлайуста с примерами 
|
Всего сообщений: 1 | Присоединился: ноябрь 2007 | Отправлено: 28 нояб. 2007 19:49 | IP
|
|
Guest
Новичок
|
Кто может написать закон негармонических вращательных колебаний. Очень нужно. Заранее благодарен.
|
Всего сообщений: Нет | Присоединился: Never | Отправлено: 28 нояб. 2007 20:32 | IP
|
|
Guest
Новичок
|
Может кто нить объяснить как из ДУ: Tdx(t)/dt+x(t)=K*1(t) получилось общее решение следующего вида.
x(t)=K(1-exp(-t/T))
где:
K,T – const
1(t) = 0 при t<0
1(t) = 1 при t>=0.
Заранее благодарен.
|
Всего сообщений: Нет | Присоединился: Never | Отправлено: 6 дек. 2007 17:45 | IP
|
|
Maggy
Новичок
|
Помогите найти общее решение дифференциального уравнения: y''- 3* y'/x=0
|
Всего сообщений: 1 | Присоединился: декабрь 2007 | Отправлено: 10 дек. 2007 21:43 | IP
|
|
Trushkov
Долгожитель
|
Цитата: Maggy написал 10 дек. 2007 21:43
Помогите найти общее решение дифференциального уравнения: y''- 3* y'/x=0
Сделайте замену функции z(x)=y'(x), получите уравнение первого порядка. Которое еще и уравнение с разделяющимися переменными.
|
Всего сообщений: 273 | Присоединился: январь 2006 | Отправлено: 10 дек. 2007 22:11 | IP
|
|
Guest
Новичок
|
y'''+4y''-6y'+y=e^x
никак не получется(((
Помогите решить...
|
Всего сообщений: Нет | Присоединился: Never | Отправлено: 14 дек. 2007 16:06 | IP
|
|
Leonid22
Новичок
|
Сначяла надо найти общее решение, для этого дифференциального уравнения.
Перейдём к виду: K^3+4*K^2-6*K=0. Находим корни:
K1=0
K2=-2+10*(1/2)
K3=-2-10*(1/2)
Следователно Y0=C1+C2*e^X*(-2+10*(1/2))+C3*e^X*(-2-10*(1/2))
Найдём частное решение: где Q(x)=e^x
^y^=e^x(A).
Где А- это не определённый коэффициент.
Чтобы найти его, надо от ^y^ взять 3 раза производную и подставить в y' y'' и y''' в твоё данное уравнение, и приравнять числа, при одинаковых коэффициентах, предварително сократив всё на е^x.
Твоим ответом будет: Y=Y0+^y^
А если чесно, то это уравнение проще некуда, никто не возьмётся его решать, а я просто выпендриться решил
Мог бы всётаки справочник почитать, и тупо сделать как там сказанно.
(Сообщение отредактировал Leonid22 14 дек. 2007 16:46)
|
Всего сообщений: 9 | Присоединился: апрель 2007 | Отправлено: 14 дек. 2007 16:45 | IP
|
|
Форум
Решение дифференциальных уравнений
