natafka


Новичок
|
    
Помогите, пожалуйста.....****))))))))
y^4+4y^2+3y=(x-1)*e^x
|
Всего сообщений: 49 | Присоединился: ноябрь 2008 | Отправлено: 8 фев. 2010 17:52 | IP
|
|
natafka


Новичок
|
    
А можно еще и с этим помочь ))))))) пожалуйста....
(1-x^2)^1/2*y' =1+y^2
|
Всего сообщений: 49 | Присоединился: ноябрь 2008 | Отправлено: 8 фев. 2010 17:59 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: natafka написал 8 фев. 2010 17:59
А можно еще и с этим помочь ))))))) пожалуйста....
(1-x^2)^1/2*y' =1+y^2
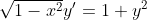
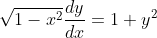
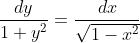
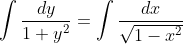
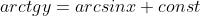
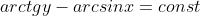
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 8 фев. 2010 19:06 | IP
|
|
natafka


Новичок
|
    
Спасибки )))))))) :***** за предыдущий RKI как всегда выручила, умничка ))))))))
Вот этот тоже никак не получается ((((( правда......
y^4+4y^2+3y=(x-1)*e^x
|
Всего сообщений: 49 | Присоединился: ноябрь 2008 | Отправлено: 8 фев. 2010 20:53 | IP
|
|
Reshalka


Новичок
|
     
natafka, если считать, что y^2=y'' тогда следует сначала решить однородное уравнение y^4+4y^2+3y=0
составляем характ. уравн.
k^4+4k^2+3=0
k^2={-3;-1}
k=(i;-i;-(корень квадр. с 3)*i;(корень квадр. с 3)*i)}
общее решение однор. получиться
y=c1*cos(x)+с2*sin(x)+c3*cos(корен кв(3)*x)+с4*sin((корен кв(3)*x))
частное решение неоднородного ищем в виде y=(ax+b)*e^x
нужно найти a и b
методом неопределённых коэффициентов
подстановкой в данное уравнение.
Общее решение Y=y(частное)+y(однородного)
(Сообщение отредактировал Reshalka 8 фев. 2010 22:31)
|
Всего сообщений: 15 | Присоединился: февраль 2010 | Отправлено: 8 фев. 2010 23:26 | IP
|
|
Snigur


Новичок
|
    
Помогите найти общее решение дифференциального уравнения
у'-у*соs х=е^(sin х)*sin(2х) и частное решение, удовлетворяющее начальному условию у=3, х=П.
(Сообщение отредактировал attention 9 фев. 2010 1:42)
|
Всего сообщений: 19 | Присоединился: июль 2009 | Отправлено: 9 фев. 2010 0:24 | IP
|
|
abm777


Новичок
|
    
Привет всем! Помогите пожалуйста! Срочно нужно решить y^2+x^2*y' = x*y*y'. Буду очень благодарна!
У кого-нибудь есть решебник к Филипову по диф.урам? Такой вообще существует? Скиньте пожалуйста ссылку, очень прошу.........
(Сообщение отредактировал attention 9 фев. 2010 1:24)
|
Всего сообщений: 8 | Присоединился: февраль 2010 | Отправлено: 9 фев. 2010 0:25 | IP
|
|
attention 


Долгожитель
|
     
Цитата: Snigur написал 8 фев. 2010 23:24
Помогите найти общее решение дифференциального уравнения
у'-у*соs х=е^(sin х)*sin(2х) и частное решение, удовлетворяющее начальному условию у=3, х=П.
Поделите обе части уравнения на e^sin(x)
^\prime y = \sin 2x \Leftrightarrow \left(e^{-\sin x}y\right)^\prime = \sin 2x \Leftrightarrow \hfill \\ \Leftrightarrow e^{ - \sin x}y = \int \sin 2x\,dx = C - \frac{1}{2}\cos 2x \Leftrightarrow \boxed{y = \left(C - \frac{1}{2}\cos 2x\right)e^{\sin x}} \hfill \\ y(\pi ) = \left(C - \frac{1}{2}\cos 2\pi } \right){e^{\sin \pi }} = 3 \Leftrightarrow C - \frac{1}{2} = 3 \Leftrightarrow C = \frac{7}{2}. \hfill \\ \boxed{y(x) = \frac{e^{\sin x}}{2}\left(7 - \cos 2x\right)} \hfill \\ \end{gathered})
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 9 фев. 2010 2:42 | IP
|
|
attention 


Долгожитель
|
     
Цитата: abm777 написал 8 фев. 2010 23:25
Привет всем! Помогите пожалуйста! Срочно нужно решить y^2+x^2*y' = x*y*y'. Буду очень благодарна!
Поделите обе части уравнения на y' и решайте относительно x

(Сообщение отредактировал attention 9 фев. 2010 15:09)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 9 фев. 2010 3:12 | IP
|
|
|
|

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)