LPechenkina

Новичок
|
    
Помогите пожалуйста с задачкой ...
Найти давление Р воздуха на высоте h=1000 м, если известно, что давление воздуха равно 1 кг на 1 см2 над уровнем моря (h=0 ) и 0,92 кг на 1 см2 на высоте h=500 м.
я нашла только что dP/dh=-kp- где p это давление h,k>0
|
Всего сообщений: 1 | Присоединился: январь 2010 | Отправлено: 23 янв. 2010 20:12 | IP
|
|
diva00


Новичок
|
    
Помогите пожалуйста решить:
Найти общее решение линейного дифференциального уравнения второго порядка с постоянными коэфициэнтами и стандартной правой частью:
у"-2у'+у=6хе^х
|
Всего сообщений: 1 | Присоединился: январь 2010 | Отправлено: 23 янв. 2010 20:48 | IP
|
|
Felis


Начинающий
|
    
Помогите решить задачу и сделать проверку!  Ну пожалуйста! Ну пожалуйста! 
y'sin^2x +y=ctgx
|
Всего сообщений: 71 | Присоединился: декабрь 2008 | Отправлено: 25 янв. 2010 19:40 | IP
|
|
lolth3

Новичок
|
     
всем привет.
ребята, как скинуть сюда отсканированую задачу?
кто знает, подскажите, как и через какой интернет-ресурс это проделывается...
|
Всего сообщений: 4 | Присоединился: январь 2010 | Отправлено: 31 янв. 2010 0:36 | IP
|
|
lolth3

Новичок
|
     

кто чем может, помогите...
|
Всего сообщений: 4 | Присоединился: январь 2010 | Отправлено: 1 фев. 2010 1:43 | IP
|
|
arina02


Новичок
|
    
пожалуйста! не могу... : найти частное решение уравнения y'tgx-y=1 удовлетворяющее начальным условиям y0=1 x0=пи/2 (Извиняюсь за "пи"! просто такие вещи только в тетрадке писала)
|
Всего сообщений: 2 | Присоединился: февраль 2010 | Отправлено: 6 фев. 2010 5:21 | IP
|
|
Reshalka


Новичок
|
     
y'tgx-y=1
Метод вариации произвольной постоянной или если легче то методом Бернулли.
Например 1-ым;
1) решение однородного уравнения
y'tgx-y=0; y'=dy/dx;
dy/y=dx/tgx
интегр. прав. и лев. часть и добавляем логарифм. констанс. зависящая от х:
ln(y)=ln(Sin(x))+ln(c(x))
y=sin(x)*c(x)
2) общее решение подстав. решен. однор.
(sin(x)*c(x))'*tg(c)-sin(x)*c(x)=1
(cos(x)*c(x)+Sin(x)*c'(x))*tg(x)-sin(x)*c(x)=1
Sin(x)*c(x)+Sin(x)*tg(x)*c'(x)-sin(x)*c(x)=1
Sin(x)*tg(x)*c'(x)=1
c(x)=integral(cos(x)/sin^2(x))+c
c(x)=-1/sin(x) + c
полученное с(x) подставл. и получаем
у=sin(x)*((-1/sin(x)) +c) или y=-1+c*sin(x)
То есть общее решение получили; Частное получим подстановкой y0 b x0 нахождением c
1=-1+с*sin(пи/2)
с=2
ответ y=-1+2*sin(x);
(Сообщение отредактировал Reshalka 6 фев. 2010 13:28)
|
Всего сообщений: 15 | Присоединился: февраль 2010 | Отправлено: 6 фев. 2010 14:18 | IP
|
|
attention 


Долгожитель
|
     
Цитата: Reshalka написал 6 фев. 2010 13:18
y'tgx-y=1
Метод вариации произвольной постоянной или если легче то методом Бернулли.
Например 1-ым;
1) решение однородного уравнения
y'tgx-y=0; y'=dy/dx;
dy/y=dx/tgx
интегр. прав. и лев. часть и добавляем логарифм. констанс. зависящая от х:
ln(y)=ln(Sin(x))+ln(c(x))
y=sin(x)*c(x)
2) общее решение подстав. решен. однор.
(sin(x)*c(x))'*tg(c)-sin(x)*c(x)=1
(cos(x)*c(x)+Sin(x)*c'(x))*tg(x)-sin(x)*c(x)=1
Sin(x)*c(x)+Sin(x)*tg(x)*c'(x)-sin(x)*c(x)=1
Sin(x)*tg(x)*c'(x)=1
c(x)=integral(cos(x)/sin^2(x))+c
c(x)=-1/sin(x) + c
полученное с(x) подставл. и получаем
у=sin(x)*((-1/sin(x)) +c) или y=-1+c*sin(x)
То есть общее решение получили; Частное получим подстановкой y0 b x0 нахождением c
1=-1+с*sin(пи/2)
с=2
ответ y=-1+2*sin(x);
Reshalka, спасибо Вам, что отвечаете!
Мне кажется, здесь проще всего разделить переменные:
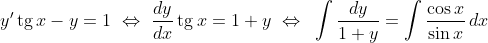
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 6 фев. 2010 22:48 | IP
|
|
arina02


Новичок
|
    
Огромное спасибо, Reshalka и attention. Решила всю контрольную, а тут что-то заклинило... Честно, впервые столкнулась с таким видом помощи, и.... не ожидала даже, что кто-то откликнется! ещё раз огромное спасибо, пошла разбираться!
|
Всего сообщений: 2 | Присоединился: февраль 2010 | Отправлено: 7 фев. 2010 9:24 | IP
|
|
Reshalka


Новичок
|
     
спасибо. я этого не анализировал поэтому пошел стандартно.
Способ действительно слишком прост, но его надо "увидеть".
|
Всего сообщений: 15 | Присоединился: февраль 2010 | Отправлено: 7 фев. 2010 12:09 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)