nastja0311
Новичок
|
   
Здравствуйте, помогите решить д.у
yy'' - (y')^2=y^4
я делаю замену y'=p,y''=pp'. тогда
ypp'-p^2=y^4;
а дальше что-то не могу понять как делать...
прошу подсказку
|
Всего сообщений: 30 | Присоединился: октябрь 2008 | Отправлено: 14 нояб. 2009 19:48 | IP
|
|
Trushkov
Долгожитель
|
  
nastja0311, после замены функции z=p^2 получится линейное уравнение первого порядка.
|
Всего сообщений: 273 | Присоединился: январь 2006 | Отправлено: 14 нояб. 2009 20:03 | IP
|
|
nastja0311
Новичок
|
ypp'-p^2=y^4
p'-p/y=y^3/p
т.е дальше делаю замену p=uv, p'=u'v+uv'
...
у меня там корни нехорошие какие-то выходят, вот я и засомневалась в правильности..
|
Всего сообщений: 30 | Присоединился: октябрь 2008 | Отправлено: 14 нояб. 2009 20:07 | IP
|
|
Selitra
Новичок
|
Добрый вечер. Помогите найти общее решение разностного уравнения второго порядка
Частное решение x(n)=0. Это вроде б неправильно. Подскажите как найти его?
|
Всего сообщений: 19 | Присоединился: декабрь 2008 | Отправлено: 14 нояб. 2009 20:27 | IP
|
|
STRELLA
Новичок
|
Господа, пожалуйста помогите решить простое диф.уравнение. Двадцать лет как ничего подобного не решал.Y```-4Y``+5Y`=0
|
Всего сообщений: 17 | Присоединился: ноябрь 2009 | Отправлено: 15 нояб. 2009 18:40 | IP
|
|
RKI 
Долгожитель
|
Цитата: STRELLA написал 15 нояб. 2009 18:40
Господа, пожалуйста помогите решить простое диф.уравнение. Двадцать лет как ничего подобного не решал.Y```-4Y``+5Y`=0
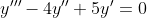
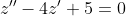
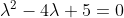
 = Ae^{-5x} + Be^{-x} )
 = Ae^{-5x} + Be^{-x} )
 = - \frac{A}{5}e^{-5x} - Be^{-x} + C )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 16 нояб. 2009 10:44 | IP
|
|
Vityok
Новичок
|
Помогите пожалуйста с решением:
1) 2xy'+y^2=1
2) xy'+y=e^x
В первом прирешении получается такое выражение:
dy/(1-y^2)=dx/(2x)
В левой части неберущийся интеграл! или может я где-то ошибся!
|
Всего сообщений: 2 | Присоединился: ноябрь 2009 | Отправлено: 16 нояб. 2009 20:59 | IP
|
|
dimax
Новичок
|
y''-2y'+5y'=(e^x)cos(2x)+(e^(2x))((x^2)-2x)+5sin(3x)
последнее найти вид решения не отыскивая коэффициенты частного решения
|
Всего сообщений: 16 | Присоединился: октябрь 2009 | Отправлено: 16 нояб. 2009 22:24 | IP
|
|
mashuny
Новичок
|
Помогите решить задачу Коши для линейного урвнения
y' + y tgx = cos^2 x
y(П/4)=1/2
|
Всего сообщений: 5 | Присоединился: март 2009 | Отправлено: 17 нояб. 2009 13:02 | IP
|
|
Kuromi
Новичок
|
Помогите решить, плиз....
Найти частные решения ур-я, указ.начальным условием
2*dy/dx=1+x^2
если у(нулевое)=0, при х(нулевое)=0
|
Всего сообщений: 1 | Присоединился: ноябрь 2009 | Отправлено: 17 нояб. 2009 14:17 | IP
|
|
Форум
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
