Форум - 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ) [41]

Форум	» Назад на решение задач по физике и термеху
Регистрация \| Профиль \| Войти \| Забытый пароль \| Присутствующие \| Справка \| Поиск

» Добро пожаловать, Гость: Войти | Регистрация

	Форум Математика 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
	Отметить все сообщения как прочитанные [ Помощь ] » Добро пожаловать на форум "Математика" «

Переход к теме
<< Назад Вперед >>

Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 ]
Модераторы: Roman Osipov, RKI, attention, paradise

RKI

Долгожитель

Цитата: itgtktdf написал 3 нояб. 2009 17:03
надо найти общее решение ДУ:
y''-2y'-2y=0

$y'' - 2y' - 2y = 0$

$\lambda^{2} - 2\lambda - 2 = 0$

$\lambda = 1 - \sqrt{3} \ \ \ \lambda = 1 + \sqrt{3}$

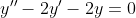
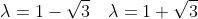
$y(x) = Ce^{(1 - \sqrt{3})x} + De^{(1 + \sqrt{3})x}$

(Сообщение отредактировал RKI 3 нояб. 2009 17:23)

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 3 нояб. 2009 17:21 | IP

RKI

Долгожитель

Цитата: Kisenochek написал 3 нояб. 2009 17:10
спасибки....очень очень помогли...вот ещё одно:
xy'-2y=x+1

$xy' - 2y = x + 1$

$xy' - 2y = 0$

$xy' = 2y$

$\frac{xdy}{dx} = 2y$

$\frac{dy}{y} = \frac{2dx}{x}$

$ln|y| = 2ln|x| + const$

$y = Cx^{2}$

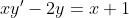
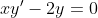
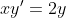
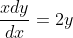
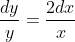
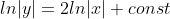
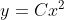
$y(x) = C(x)x^{2}$

$y'(x) = C'(x)x^{2} + 2xC(x)$

$xy' - 2y = x + 1$

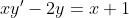
$C'(x)x^{3} + 2C(x)x^{2} - 2C(x)x^{2} = x + 1$

$C'(x) = \frac{1}{x^{2} } + \frac{1}{x^{3} }$

$C(x) = - \frac{1}{x} - \frac{1}{2x^{2} } + D$

$y(x) = C(x)x^{2}$

$y(x) = Dx^{2} - x - \frac{1}{2}$

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 3 нояб. 2009 17:30 | IP

vikusya

Новичок
Помогите пожалуйста решить:
разложить в ряд Фурье переодическую функцию f(x), заданную на интервале-периоде

{-(x+2) при -2<(меньше или равно)x<(меньше или равно) 0
f(x)=
{-(x-2) при -0<(меньше)x<(меньше)2

Всего сообщений: 12 | Присоединился: ноябрь 2009 | Отправлено: 3 нояб. 2009 17:59 | IP

Fenja544

Новичок
1. Исследовать сходимость числового ряда:
беск.
СУММ n3 / (2n)!
n=1
2. Найти область сходимости степенного ряда:
беск.
СУММ ((x-2)^n)/ n*(n+1)
n=1

3. Вычислить определенный интеграл с точностью до 0,001. Для этого подынтегральную функцию разложить в степенной ряд, который затем почленно проинтегрировать:
0,5
int x*ln(1+x^2)dx
0

Всего сообщений: 40 | Присоединился: октябрь 2009 | Отправлено: 3 нояб. 2009 18:20 | IP

itgtktdf

Новичок
спасибо большое)))а это как решать???
(2x+y)y'=y M(1;1)
знаю только что:Однородное уравнение:

(2x+y)y'=y, y'=y/(2x+y), замена: z=y/x.
а как записать...

Всего сообщений: 22 | Присоединился: ноябрь 2009 | Отправлено: 3 нояб. 2009 19:17 | IP

Kisenochek

Новичок
Благодарю!!!помогите пожалуйста.....
y''+5y'+6y=1/1+e^(2x)
y(0)=ТТ(пи)/4+1/2ln^2 y'(0)=-3/4ТТ

Всего сообщений: 16 | Присоединился: ноябрь 2009 | Отправлено: 3 нояб. 2009 19:29 | IP

bukashka

Новичок
Помогите, пожалуйста...
Найти общий интеграл ДУ( ответ в виде Ф(x,y)-c)
2xdx-ydy=y(x^2)dy-x(y^2)dx

Всего сообщений: 13 | Присоединился: октябрь 2009 | Отправлено: 4 нояб. 2009 0:35 | IP

RKI

Долгожитель

Цитата: bukashka написал 4 нояб. 2009 0:35
Помогите, пожалуйста...
Найти общий интеграл ДУ( ответ в виде Ф(x,y)-c)
2xdx-ydy=y(x^2)dy-x(y^2)dx

$2xdx - ydy = yx^{2}dy - xy^{2}dx$

$2x - yy' = yx^{2}y' - xy^{2}$

$yx^{2}y' + yy' = 2x + xy^{2}$

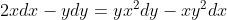
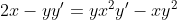
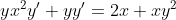
$y(x^{2} + 1)y' = x(2 + y^{2} )$

$y(x^{2} + 1)\frac{dy}{dx} = x(2 + y^{2})$

$\frac{ydy}{2 + y^{2} } = \frac{xdx}{1 + x^{2} }$

**
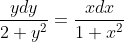
$\int\frac{ydy}{2 + y^{2} } = \frac{1}{2}\int\frac{d(2 + y^{2})}{2 + y^{2} } = \frac{1}{2}ln(2 + y^{2}) + const$

$\int\frac{xdx}{1 + x^{2} } = \frac{1}{2}\int\frac{d(1 + x^{2})}{1 + x^{2} } = \frac{1}{2}ln(1 + x^{2}) + const$
**

$\frac{1}{2}ln(2 + y^{2}) = \frac{1}{2}ln(1 + x^{2}) + const$

$ln(2 + y^{2}) = ln(1 + x^{2}) + const$

$ln(2 + y^{2}) - ln(1 + x^{2}) = const$

$ln\frac{2 + y^{2} }{1 + x^{2} } = const$

$\frac{2 + y^{2} }{1 + x^{2} } = const$

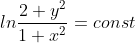
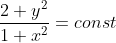
(Сообщение отредактировал RKI 4 нояб. 2009 11:50)

Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 4 нояб. 2009 11:49 | IP

vikusya

Новичок
Помогите пожалуйста решить:
разложить в ряд Фурье переодическую функцию f(x), заданную на интервале-периоде

{-(x+2) при -2<(меньше или равно)x<(меньше или равно) 0
f(x)=
{-(x-2) при -0<(меньше)x<(меньше)2

Всего сообщений: 12 | Присоединился: ноябрь 2009 | Отправлено: 4 нояб. 2009 12:03 | IP

kraslex

Новичок
Проверьте, пожалуйста решение
y''-2y+y=8e^x
Найти общее решение диф. уравнения
Решение
у^2-2у+у=(у-1)^2
к=1
у0=(С1х+С2)е^х
f(x)=8e^x
a=1. n=0
yч=х^2Q0(x)e^ax
Q0(x)=A
1 |yч=Ах^2е^х
-2|yч'=2Ае^х+2Ах^2е^х=2А(х+х^2)е^х
1 |уч''=2А(1+2х)е^х+4А(х+х^2)е^х=2А(1+4х+2х^2)е^х
Ау^х(2(1+4х+2х^2)-4(х+х^2)+х^2)=8е^х
Ау^х=8у^х
А=8
Частное решение
уч=8х^2е^х
Общее решение
у=уч+у0=8х^2е^х+(С1х+С2)у^ч
''

Всего сообщений: 22 | Присоединился: ноябрь 2009 | Отправлено: 4 нояб. 2009 13:00 | IP