vovancheg


Новичок
|
     
RKI спасибо большое)))))
|
Всего сообщений: 6 | Присоединился: ноябрь 2009 | Отправлено: 3 нояб. 2009 9:01 | IP
|
|
vikusya


Новичок
|
    
помогите решить пожалуйста
1) даны Д.у. 2-ого порядка допускающие понижение порядка. Найти частное решение Д.у. удовлетворяющее начальным условиям.
y"+у'tgx=cosx y(0)=1 у'(0)=0
2)даны линейные неоднородные Д.у. 2-ого порядка с постоянными коэфицентами. Найти частное решение Д.у. удовлетворяющее начальным условиям
y"-4y=4sin2x y(0)=2 у'(0)=7
3) разложить в ряд Фурье переодическую функцию f(x), заданную на интервале-периоде
{-(x+2) при -2<(меньше или равно)x<(меньше или равно) 0
f(x)=
{-(x-2) при -0<(меньше)x<(меньше)2
|
Всего сообщений: 12 | Присоединился: ноябрь 2009 | Отправлено: 3 нояб. 2009 9:41 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: Fenja544 написал 2 нояб. 2009 18:44
3. y'' - 6*y' + 9*y = e^(3*x), y(0)=1, y'(0)=0


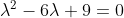
^{2} = 0 )
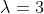 - корень кратности 2 - корень кратности 2
e^{3x} )

e^{3x} = (ax^{3} + bx^{2})e^{3x} )
e^{3x} + 3(ax^{3} + bx^{2})e^{3x} = (3ax^{2} + 2bx + 3ax^{3} + 3bx^{2})e^{3x} )
e^{3x} + 3(3ax^{2} + 2bx + 3ax^{3} + 3bx^{2})e^{3x} = )
e^{3x} = (9ax^{3} + 18ax^{2} + 9bx^{2} + 6ax + 12bx + 2b)e^{3x} )
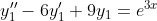
e^{3x} - 6(3ax^{2} + 2bx + 3ax^{3} + 3bx^{2})e^{3x} + 9(ax^{3} + bx^{2})e^{3x} = e^{3x} )
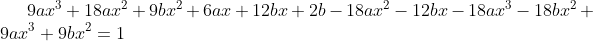
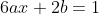

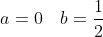
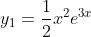
 = y_{0} + y_{1} )
 = (Cx + D + \frac{1}{2}x^{2})e^{3x} )
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 3 нояб. 2009 9:52 | IP
|
|
vikusya


Новичок
|
    
(Сообщение отредактировал vikusya 3 нояб. 2009 10:01)
|
Всего сообщений: 12 | Присоединился: ноябрь 2009 | Отправлено: 3 нояб. 2009 10:00 | IP
|
|
itgtktdf

Новичок
|
     
спасибо огромное приогромное)))))
ну вот ещё пример не получается:
1) (2x+y)y'=y M(1;1)
2) y'''(x+2)^5+24=0
буду очень благодарна
(Сообщение отредактировал itgtktdf 3 нояб. 2009 11:29)
|
Всего сообщений: 22 | Присоединился: ноябрь 2009 | Отправлено: 3 нояб. 2009 10:20 | IP
|
|
Kisenochek


Новичок
|
     
здравствуйте))))помогите с уравнением,не могу решить:
1) xy'+y=x^(2)y^(2) y(1)=0,5
2) 3x^(2)e^(y)dx+(x^(3)e^y-1)dy=0
заранее спасибо!!!
|
Всего сообщений: 16 | Присоединился: ноябрь 2009 | Отправлено: 3 нояб. 2009 11:13 | IP
|
|
vikusya


Новичок
|
    
помогите решить пожалуйста
1) даны Д.у. 2-ого порядка допускающие понижение порядка. Найти частное решение Д.у. удовлетворяющее начальным условиям.
y"+у'tgx=cosx y(0)=1 у'(0)=0
2)даны линейные неоднородные Д.у. 2-ого порядка с постоянными коэфицентами. Найти частное решение Д.у. удовлетворяющее начальным условиям
y"-4y=4sin2x y(0)=2 у'(0)=7
3) разложить в ряд Фурье переодическую функцию f(x), заданную на интервале-периоде
{-(x+2) при -2<(меньше или равно)x<(меньше или равно) 0
f(x)=
{-(x-2) при -0<(меньше)x<(меньше)2
|
Всего сообщений: 12 | Присоединился: ноябрь 2009 | Отправлено: 3 нояб. 2009 15:02 | IP
|
|
Fenja544


Новичок
|
     
RKI - Вы чудо!!!
|
Всего сообщений: 40 | Присоединился: октябрь 2009 | Отправлено: 3 нояб. 2009 15:03 | IP
|
|
Fenja544


Новичок
|
     
Помогите, пожалуйста, решить:
1. Применяя интегральные формулы Коши, вычислить интегралы по замкнутому контуру y(гамма),пробегаемому против часовой стрелки. I=1/(2*п*i) int dz/(z^2*(z-3)) , y(гамма): |z-i|=5
2. Разложить данную функцию в ряд Лорана в окрестности указанной точки z0 и определить область сходимости этого разложения. f(z) = 1/((z^2+1)^2) , z0 = бесконечность
|
Всего сообщений: 40 | Присоединился: октябрь 2009 | Отправлено: 3 нояб. 2009 15:08 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: vikusya написал 3 нояб. 2009 9:41
1) даны Д.у. 2-ого порядка допускающие понижение порядка. Найти частное решение Д.у. удовлетворяющее начальным условиям.
y"+у'tgx=cosx y(0)=1 у'(0)=0

 = z(x) )
 = z'(x) )

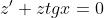
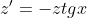

dx )
**
dx = \int\frac{-(sinx)dx}{cosx} = \int \frac{d(cosx)}{cosx} = ln|cosx| + const )
**
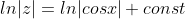
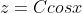
 = C(x)cosx )
 = C'(x)cosx - C(x)sinx )

cosx - C(x)sinx + C(x)sinx = cosx )
 = 1 )
 = x + D )
 = C(x)cosx )
 = Dcosx + xcosx )
 = Dcosx + xcosx )
 = 0 )
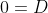
 = xcosx )
 = \int xcosxdx = \int xd(sinx) = )
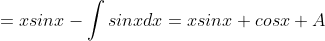
 = 1 )
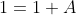
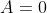
 = xsinx + cosx )
(Сообщение отредактировал RKI 3 нояб. 2009 16:08)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 3 нояб. 2009 16:07 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)

 Форум
Форум

 Математика
Математика

 2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)
2.3.1 Обыкновенные дифференциальные уравнения (ОДУ)