Форум - 2.1.6 Первообразная (неопределенный интеграл) [50]

Форум	» Назад на решение задач по физике и термеху
Регистрация \| Профиль \| Войти \| Забытый пароль \| Присутствующие \| Справка \| Поиск

» Добро пожаловать, Гость: Войти | Регистрация

	Форум Математика 2.1.6 Первообразная (неопределенный интеграл)
	Отметить все сообщения как прочитанные [ Помощь ] » Добро пожаловать на форум "Математика" «

Переход к теме
<< Назад Вперед >>

Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 ]
Модераторы: Roman Osipov, RKI, attention, paradise

ustam

Долгожитель

Цитата: lara13091978 написал 13 фев. 2011 23:32

∫▒(x-1)dx/(√x(4+√x))=∫▒〖(t^2-1)2tdt/(t(4+t))=2∫▒〖((t^2-16)+15)dt)/(4+t)=2∫▒〖(t-4)dt+2∫▒〖15/(t-4) dt=2/3 t^3+30ln|t-4|+c=2/3 x√x+30ln|√x-4|+c〗〗〗〗

У меня получается иначе.
∫(x-1)dx/(√x(4+√x))=∫(t^2-1)2tdt/(t(4+t))=2∫(t^2-1)dt/(4+t)=
=2∫[t-4+15/(t+4)]dt=2(t^2/2 -4t+15ln|t+4|) +C=t^2 -8t+30ln|t+4|+C=
=x-8√x+30ln|√x+4|+C
Проверял дифференцированием: получается подынтегральное выражение

Всего сообщений: 420 | Присоединился: декабрь 2008 | Отправлено: 14 фев. 2011 0:20 | IP

alex6ndr

Новичок
Здравствуйте!
Распишите пожалуйста ход интегрирования функции x^2/(x^6+1)

Заранее спасибо!

Всего сообщений: 1 | Присоединился: февраль 2011 | Отправлено: 16 фев. 2011 13:55 | IP

ustam

Долгожитель

Цитата: alex6ndr написал 16 фев. 2011 13:55

Подстановка: t= х^3, тогда dt = 3x^2dx
∫x^2dx/(x^6 +1) = (1/3)∫dt/(t^2 +1) = (1/3)arctgt +C=(1/3)arctgx^3 +C

Всего сообщений: 420 | Присоединился: декабрь 2008 | Отправлено: 16 фев. 2011 20:17 | IP

Umnica

Новичок
Помогите пожалуйста регить интегралы..

Заранее спасибо!

Всего сообщений: 8 | Присоединился: февраль 2011 | Отправлено: 26 фев. 2011 13:17 | IP

Lyuda

Начинающий
Потренеруюсь вставлять формулы
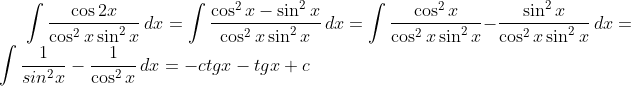
1) $\int\frac{\cos 2x}{\cos^2x\sin^2x}\,dx=\int\frac{\cos ^2x-\sin^2x}{\cos^2x\sin^2x}\,dx=\int\frac{\cos ^2x}{\cos^2x\sin^2x}-\frac{\sin^2x}{\cos^2x\sin^2x}\,dx=\int\frac{1}{sin^2x}-\frac{1}{\cos^2x}\,dx=-ctgx-tgx+c$

(Сообщение отредактировал Lyuda 1 марта 2011 19:08)

Всего сообщений: 73 | Присоединился: ноябрь 2007 | Отправлено: 1 марта 2011 17:49 | IP

Lyuda

Начинающий
2) $\int\frac{2x-3}{\sqrt{4+x^2}}\,dx=\int\frac{dx^2}{\sqrt{4+x^2}}-3\int\frac{dx}{\sqrt{4+x^2}}=\int{(4+x^2)^{-1/2}d(4+x^2)}-3\int\frac{dx}{\sqrt{4+x^2}}=2\sqrt{(4+x^2)}-3\ln|x+\sqrt{4+x^2}|+c$

(Сообщение отредактировал Lyuda 1 марта 2011 19:06)

Всего сообщений: 73 | Присоединился: ноябрь 2007 | Отправлено: 1 марта 2011 19:01 | IP

Lyuda

Начинающий
3) $\int\frac{dx}{x^2+4x+20}}=\int\frac{dx}{x^2+4x+4+16}}=\int\frac{dx}{(x+2)^2+16}}=\int\frac{d(x+2)}{(x+2)^2+16}}=\frac{1}{4}arctg\frac{x+2}{4}+c$

(Сообщение отредактировал Lyuda 1 марта 2011 19:13)

Всего сообщений: 73 | Присоединился: ноябрь 2007 | Отправлено: 1 марта 2011 19:12 | IP

Sia

Новичок
помогите! я уже голову сломала, не знаю, как решать

1) (x^4+1)/(x^3-x^2+x-1)

2) 1/(1-cos(x))

3) 1/(1+cos^2(x))

Всего сообщений: 3 | Присоединился: март 2011 | Отправлено: 27 марта 2011 1:14 | IP

Besna

Начинающий

Цитата: Sia написал 27 марта 2011 1:14

1) (x^4+1)/(x^3-x^2+x-1) - к знаменателю примените формулу Сумма кубов. Затем его преобразуйте.
2) 1/(1-cos(x)) = -x/cosx-1

Всего сообщений: 61 | Присоединился: февраль 2011 | Отправлено: 28 марта 2011 21:19 | IP

Sia

Новичок

Цитата: Besna написал 28 марта 2011 21:19
Цитата: Sia написал 27 марта 2011 1:14

1) (x^4+1)/(x^3-x^2+x-1) - к знаменателю примените формулу Сумма кубов. Затем его преобразуйте.
2) 1/(1-cos(x)) = -x/cosx-1

1/(1-cos(x)) = -x/cosx-1
я не очень поняла как получилось, можешь сказать каким способом ты решил?

Всего сообщений: 3 | Присоединился: март 2011 | Отправлено: 29 марта 2011 1:18 | IP

Отправка ответа:

Имя пользователя Вы зарегистрировались?
Пароль Забыли пароль?
Сообщение
Использование HTML запрещено
Использование IkonCode разрешено
Смайлики разрешены

Опции отправки
Добавить подпись?
Получать ответы по e-mail?
Разрешить смайлики в этом сообщении?
Просмотреть сообщение перед отправкой? Да Нет

Переход к теме
<< Назад Вперед >> Несколько страниц [ 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 ]