Olegmath2

Полноправный участник
|
     
Цитата: Mixailo написал 22 марта 2009 15:35
Здравствуйте. Помогите пожалуйста вычислить два предела
1). lim ln(cos3x)/ln(cosx); x->0
2). lim ln(1+2x)/ln(x); x->0
Условие второй задачи не корректно!
Функция f(x)=ln(1+2x)/ln(x) определена на множестве
(0;1)U(1;+бесконечн.). Может речь идёт о правостороннем пределе функции f(x) в точке x=0?
|
Всего сообщений: 235 | Присоединился: февраль 2009 | Отправлено: 22 марта 2009 17:37 | IP
|
|
Mixailo

Новичок
|
     
Извиняюсь. во втором примере lim ln(1+2x)/х
|
Всего сообщений: 32 | Присоединился: июль 2008 | Отправлено: 22 марта 2009 18:03 | IP
|
|
Mixailo

Новичок
|
     
Спасибо. Решил.
Скажите только. в первом примере отвте 9 или 1\9?
|
Всего сообщений: 32 | Присоединился: июль 2008 | Отправлено: 22 марта 2009 18:23 | IP
|
|
Olegmath2

Полноправный участник
|
     
Цитата: Mixailo написал 22 марта 2009 18:23
Спасибо. Решил.
Скажите только. в первом примере отвте 9 или 1\9?
В первом примере ответ 9.
|
Всего сообщений: 235 | Присоединился: февраль 2009 | Отправлено: 22 марта 2009 18:36 | IP
|
|
Mixailo

Новичок
|
     
(( У меня 1\9. Где ошибка?
lim ln(cos3x)/ln(cosx); x->0
lim (1/ln(cosx))'*(ln(cos3x))'
lim sinx/(3*sin3x)
x/9x=1/9
|
Всего сообщений: 32 | Присоединился: июль 2008 | Отправлено: 22 марта 2009 21:14 | IP
|
|
Olegmath2

Полноправный участник
|
     
Цитата: Mixailo написал 22 марта 2009 21:14
(( У меня 1\9. Где ошибка?
lim ln(cos3x)/ln(cosx); x->0
lim (1/ln(cosx))'*(ln(cos3x))'
lim sinx/(3*sin3x)
x/9x=1/9
lim{x->0} ln(cos3x)/ln(cosx)=lim{x->0} (ln(cos3x))'/(ln(cosx))'=
=lim{x->0} (-3tg(3x))/(-tg(x))=lim{x->0} (3tg(3x)/x)/(tg(x)/x)=
=lim{x->0} (9tg(3x)/(3x))/(tg(x)/x)=9/1=9.
(Сообщение отредактировал Olegmath2 22 марта 2009 23:19)
|
Всего сообщений: 235 | Присоединился: февраль 2009 | Отправлено: 22 марта 2009 23:17 | IP
|
|
daimos


Новичок
|
      
Помогите пожалуйста решить лимиты
внешняя ссылка удалена
внешняя ссылка удалена
Зарание большое спасибо, сам просто туго отстрелюю их
|
Всего сообщений: 19 | Присоединился: декабрь 2008 | Отправлено: 25 окт. 2009 15:12 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: daimos написал 25 окт. 2009 15:12
Помогите пожалуйста решить лимиты
внешняя ссылка удалена
внешняя ссылка удалена
Зарание большое спасибо, сам просто туго отстрелюю их
}{x^{5} (\frac{100}{x^{4} } + 101)} = )
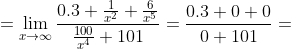
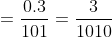
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 16:42 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: daimos написал 25 окт. 2009 15:12
Помогите пожалуйста решить лимиты
внешняя ссылка удалена
внешняя ссылка удалена
Зарание большое спасибо, сам просто туго отстрелюю их
(x^{2} + 2x + 1)}{(x-2)(x^{2} + 2x + 4)} = )
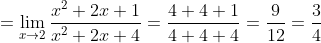
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 16:47 | IP
|
|
RKI 


Долгожитель
|
    
Цитата: daimos написал 25 окт. 2009 15:12
Помогите пожалуйста решить лимиты
внешняя ссылка удалена
внешняя ссылка удалена
Зарание большое спасибо, сам просто туго отстрелюю их
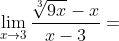
(\sqrt[3]{81x^{2} } + x\sqrt[3]{9x} + x^{2})}{(x-3)(\sqrt[3]{81x^{2} } + x\sqrt[3]{9x} + x^{2})} = )
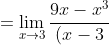(\sqrt[3]{81x^{2} } + x\sqrt[3]{9x} + x^{2})} = )
 }{(x-3)(\sqrt[3]{81x^{2} } + x\sqrt[3]{9x} + x^{2})} = )
(3+x)}{(x-3)(\sqrt[3]{81x^{2} } + x\sqrt[3]{9x} + x^{2})} = )
}{\sqrt[3]{81x^{2} } + x\sqrt[3]{9x} + x^{2} } = )
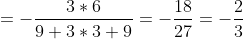
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 25 окт. 2009 16:55 | IP
|
|

 Форум
Форум

 Математика
Математика

 Вычисление пределов
Вычисление пределов

 Форум
Форум

 Математика
Математика

 Вычисление пределов
Вычисление пределов