paradise 

Долгожитель
|
       
Цитата: anvar написал 12 окт. 2011 18:39
и это если можете?
Найти производную третьего порядка
y=(2x+3)ln^2*x ,
* умножить, ^ в степени
y' = ((2x+3)ln^2*x)' = (2x+3)' * (lnx)^2 + (2x+3) * ((lnx)^2)' = 2*(lnx)^2 + (2x+3)*(2lnx)*(1/x)
|
Всего сообщений: 428 | Присоединился: ноябрь 2008 | Отправлено: 18 окт. 2011 9:50 | IP
|
|
nasya

Новичок
|
     
Пожалуйста, помогите найти производные. Заранее очень благодарна
y=2√(1-√x)/(1+√x)
y=√((3-x)*(2+x) )+5arcsin√(x+2)/5
y=(sincos3*(cos)^2 2x))/4sin4x
|
Всего сообщений: 1 | Присоединился: декабрь 2011 | Отправлено: 11 дек. 2011 0:05 | IP
|
|
voidperf

Новичок
|
      
Помогите найти наиб. и наим. значения ф-ции

|
Всего сообщений: 1 | Присоединился: декабрь 2011 | Отправлено: 11 дек. 2011 12:36 | IP
|
|
student himik


Новичок
|
     
Помогите пожалуйста для этих v функций:
внешняя ссылка удалена
найти углы наклона касательных, проведённых в точках графиков, которые соответствуют точкам перегиба. Как мог по-русски обьяснил 
|
Всего сообщений: 3 | Присоединился: декабрь 2011 | Отправлено: 11 дек. 2011 18:57 | IP
|
|
lizka340

Новичок
|
      
помогите пожалуйста решить пример
Извините, не разобралась как вставлять формулы правильно..
Найти общее решение уравнения
xy´-y=x tg y/x
|
Всего сообщений: 2 | Присоединился: декабрь 2011 | Отправлено: 15 дек. 2011 14:15 | IP
|
|
sharm


Новичок
|
      
Прошу подсказать и помочь в поиске производных заданных функций:
а) Дано: 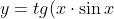)
у меня вот что получается:

но думаю что-то не то...
б) Дано: 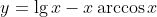
получается:
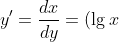' - (x\arccos x)' = \frac{1}{{x\ln 10}} - \frac{1}{{\sqrt {1 - {x^2}} }})
дальше тупик...
в) Дано: 
тут тупик, не знаю как по какой формуле дифференцировать функцию: по показательной  или степенной или степенной 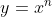 ? ?
г) Дано:

получается:
'}}{{(\sqrt \pi \cdot x)'}} = \frac{{3{x^2}}}{{\frac{x}{{2\sqrt \pi }} + \sqrt \pi }} = \frac{{6{x^2}\sqrt \pi }}{{x + 2\pi }})
добавлено:
с первым вроде разобрался (нужно было через сложную делать), получилось так: 2/sin2x
помогите с остальными пожалуйста
(Сообщение отредактировал sharm 7 янв. 2012 21:16)
|
Всего сообщений: 20 | Присоединился: декабрь 2011 | Отправлено: 7 янв. 2012 17:53 | IP
|
|
deeyavol

Новичок
|
     
Помогите, пожалуйста найти производную
у=2/7*x^3*x^1/2 -4/11*x^5*x+ 2/15*x^7*x^1/2
у=(x^2 +2*x+2)е^(-х)
у=2^(3*х)/3^(2*х)
|
Всего сообщений: 2 | Присоединился: январь 2012 | Отправлено: 14 янв. 2012 17:36 | IP
|
|
Lyuda

Начинающий
|
       
Цитата: sharm написал 7 янв. 2012 17:53
Прошу подсказать и помочь в поиске производных заданных функций:
а) Дано: 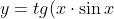)
у меня вот что получается:

но думаю что-то не то...
б) Дано: 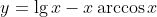
получается:
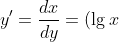' - (x\arccos x)' = \frac{1}{{x\ln 10}} - \frac{1}{{\sqrt {1 - {x^2}} }})
дальше тупик...
в) Дано: 
тут тупик, не знаю как по какой формуле дифференцировать функцию: по показательной  или степенной или степенной 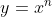 ? ?
г) Дано:

получается:
'}}{{(\sqrt \pi \cdot x)'}} = \frac{{3{x^2}}}{{\frac{x}{{2\sqrt \pi }} + \sqrt \pi }} = \frac{{6{x^2}\sqrt \pi }}{{x + 2\pi }})
добавлено:
с первым вроде разобрался (нужно было через сложную делать), получилось так: 2/sin2x
помогите с остальными пожалуйста
a)
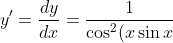}}(\sin x+x\cos x))
б)
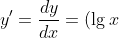' - (x\arccos x)' = \frac{1}{{x\ln 10}}-\arccos x+ x\frac{1}{{\sqrt {1 - {x^2}} }})
в)


г)
'{(\sqrt \pi \cdot x)}-{(1 - {x^3})}({\sqrt \pi \cdot x)'}}}{{(\sqrt \pi \cdot x)^2}} = )
}\sqrt \pi }}{\pi x^2} )
(Сообщение отредактировал Lyuda 15 янв. 2012 14:49)
|
Всего сообщений: 73 | Присоединился: ноябрь 2007 | Отправлено: 15 янв. 2012 14:39 | IP
|
|
dirom

Новичок
|
     
Помогите пожалуйста с решением.
вычислите все частные производные второго порядка
u=(cos^2)*(zxy)+z^xy
Буду бесконечно благодарна!
(Сообщение отредактировал dirom 10 фев. 2012 19:55)
|
Всего сообщений: 13 | Присоединился: ноябрь 2011 | Отправлено: 10 фев. 2012 18:31 | IP
|
|
ELENA 20


Новичок
|
      
Ребята помогите блондинке решить задания.Пожалуйста, пожалуйста, пожалуйста.....
1) yy′ =(1+e^x), y(0)=1
2) y′ - (2y/x+1)= (x+1)^3
|
Всего сообщений: 6 | Присоединился: декабрь 2011 | Отправлено: 1 марта 2012 22:11 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.3 Производные и дифференциалы
2.1.3 Производные и дифференциалы

 Форум
Форум

 Математика
Математика

 2.1.3 Производные и дифференциалы
2.1.3 Производные и дифференциалы