ProstoVasya

Долгожитель
|
     
KrisRu
1) При x<0 ряд расходится. При не отрицательных х остаток ряда допускает равномерную оценку. Следовательно, ряд равномерно сходится при x>=0.
2) Примените признак Дирихле.
3) Примените признак Абеля.
Исследование сходимости во всех оставшихся задачах проводится одинаково. На вторых множествах Е_2 сходимость равномерная, т.к. эти ряды мажорируются числовыми сходящимися рядами.
На первых промежутках Е_1 равномерной сходимости нет из-за точки 0, т.к. любой остаток этих рядов при х->0 не может быть сколь угодно малым.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 24 сен. 2009 23:22 | IP
|
|
KrisRu

Новичок
|
     
спасибо, хоть я сделала уже сама, проверка не помешает никогда...
|
Всего сообщений: 14 | Присоединился: сентябрь 2009 | Отправлено: 25 сен. 2009 0:10 | IP
|
|
KrisRu

Новичок
|
     
Сходмость у меня что-то не идет, помогите разобраться хоть с частью примеров...

|
Всего сообщений: 14 | Присоединился: сентябрь 2009 | Отправлено: 27 сен. 2009 22:03 | IP
|
|
attention 


Долгожитель
|
      
Для KrisRu
5)

В граничных точках интервала сходимости ряд сходится:
- при x=-1, по теореме Лейбница:

- при x=1 сравниваем ряд с рядом обратных квадратов, который сходится согласно интегральному признаку Коши.
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 28 сен. 2009 17:56 | IP
|
|
attention 


Долгожитель
|
      
Цитата: KrisRu написал 27 сен. 2009 21:03
Сходмость у меня что-то не идет, помогите разобраться хоть с частью примеров...
7. Определить радиус и интервал сходимости и исследовать поведение в граничных точках интервала сходимости следующего степенного ряда:

Представим ряд в виде суммы двух рядов, т.к.

То есть имеем:

Обозначим общие члены рядов в правой части равенства:
 и и 
Тогда исходный ряд сходится, если сходятся ряды с общими членами  и и  , и расходится, если расходится хотя бы один из рядов с общим членом , и расходится, если расходится хотя бы один из рядов с общим членом  или или  ; а интервалом сходимости исходного ряда будет тот интервал, который является пересечением интервалов сходимости рядов с общими членами ; а интервалом сходимости исходного ряда будет тот интервал, который является пересечением интервалов сходимости рядов с общими членами  и и  . .
Теперь найдем радиусы и интервалы сходимости рядов с общими членами  и и  : :
1)

2)

Следовательно, исходный ряд имеет такие радиус и интервал сходимости:

Так как ряд с общим членом  заведомо сходится при заведомо сходится при
 , ,
то, следовательно, чтобы выяснить поведение исходного ряда в граничных точках интервала сходимости, надо выяснить поведение ряда с общим членом  в этих точках интервала сходимости. Но в граничных точках ряд с общим членом в этих точках интервала сходимости. Но в граничных точках ряд с общим членом  равен гармоническому ряду: равен гармоническому ряду:
 , ,
который, как известно, расходится.
(Сообщение отредактировал attention 28 сен. 2009 20:21)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 28 сен. 2009 20:49 | IP
|
|
deffect


Новичок
|
     
помогите пожалуйсто решить контрольную, пары посещаю ничего не понимаю((((в понедельник уже сдавать а у меня ничего не решено
часть1
   
|
Всего сообщений: 4 | Присоединился: сентябрь 2009 | Отправлено: 29 сен. 2009 15:41 | IP
|
|
RKI 


Долгожитель
|
     
deffect Задание 2. 5.1.
^{n} }{n\sqrt[3]{n} } )
Данный ряд является знакопеременным. Члены данного ряда имеют вид:
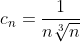
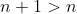
Кубический корень является возрастающей функцией. Следовательно,
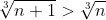
\sqrt[3]{n+1} > n\sqrt[3]{n} \ \ \Rightarrow \ \ \frac{1}{(n+1)\sqrt[3]{n+1} } < \frac{1}{n\sqrt[3]{n} } \ \ \Rightarrow \ \ c_{n+1} < c_{n} )
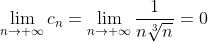
По теореме Лейбница исходный ряд ^{n} }{n\sqrt[3]{n} } ) сходится сходится
^{n}|}{|n\sqrt[3]{n}|} = \sum\limits_{n=1}^{+\infty} \frac{1}{n\sqrt[3]{n} } )
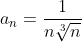
 = \frac{1}{x\sqrt[3]{x} }, x \ge 1 )
 = a_{n} )
Функция f(x) является непрерывной, положительной и монотонно убывающей на заданной области определения.
 = \int f(x)dx = \int \frac{dx}{x\sqrt[3]{x} } = - \frac{3}{\sqrt[3]{x} } )
 = \lim\limits_{x \to +\infty} - \frac{3}{\sqrt[3]{x} } = 0 )
По интегральному признаку Маклорена-Коши ряд 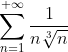 сходится. сходится.
Следовательно, исходный ряд ^{n} }{n\sqrt[3]{n} } ) является абсолютно сходящимся является абсолютно сходящимся
(Сообщение отредактировал RKI 30 сен. 2009 10:57)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 30 сен. 2009 10:44 | IP
|
|
RKI 


Долгожитель
|
     
deffect Задание 2. 5.3
^{n} n}{n+5} )
Данный ряд является знакопеременным. Члены данного ряда имеют вид (учитывая знак):
^{n} n}{n+5} )
^{n+1} (n+1)}{n+6} )
(n+5)}{n(n+6)} = )
(1 + \frac{5}{n})}{1 + \frac{6}{n} } = - \frac{(1+0)(1+0)}{1+0} = - 1 < 1 )
По признаку Даламбера исходный ряд ^{n} n}{n+5} ) сходится сходится
^{n} n|}{|n+5|} = \sum\limits_{n=1}^{+\infty} \frac{n}{n+5} )
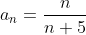

Следовательно, нарушается необходимое условие сходимости ряда. Следовательно ряд 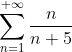 заведомо расходится. заведомо расходится.
Это означает, что исходный ряд ^{n} n}{n+5} ) абсолютно не сходится абсолютно не сходится
(Сообщение отредактировал RKI 30 сен. 2009 11:20)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 30 сен. 2009 11:12 | IP
|
|
RKI 


Долгожитель
|
     
deffect Задание 3. 5.1
!} = \sum\limits_{n=1}^{+\infty} \frac{x^{n} x^{4} }{(n-2)!} = x^{4} \sum\limits_{n=1}^{+\infty} \frac{x^{n} }{(n-2)!} )
Найдем радиус R сходимости исходного степенного ряда.
!} )
!} )
!}{(n-2)!} = \lim\limits_{n \to +\infty} \frac{(n-1)(n-2)!}{(n-2)!} = )
 = +\infty )
Следовательно, исходный ряд !} ) сходится на всей числовой оси сходится на всей числовой оси
(Сообщение отредактировал RKI 30 сен. 2009 11:50)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 30 сен. 2009 11:48 | IP
|
|
RKI 


Долгожитель
|
     
deffect Задание 3. 5.2
^{n} }{n+1} )
Найдем радиус R сходимости степенного ряда.
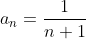

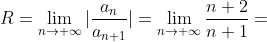
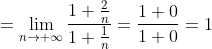
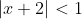


Таким образом, исходный степенной ряд ^{n} }{n+1} ) сходится на интервале сходится на интервале  )
Рассмотрим граничные точки x = - 3 и x = - 1
При x = - 1 исходный степенной ряд ^{n} }{n+1} ) принимает вид принимает вид  . Это гармоничный ряд, который является расходящимся. . Это гармоничный ряд, который является расходящимся.
Таким образом, в точке x = - 1 исходный степенной ряд ^{n} }{n+1} ) расходится. расходится.
При x = - 3 исходный степенной ряд ^{n} }{n+1} ) принимает вид принимает вид ^{n} }{n+1} ) . .
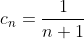
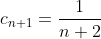
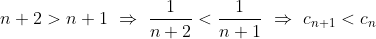
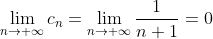
По теореме Лейбница ряд ^{n} }{n+1} ) сходится. сходится.
Следовательно, в точке x = - 3 исходный степенной ряд ^{n} }{n+1} ) сходится. сходится.
Таким образом, исходный степенной ряд ^{n} }{n+1} ) сходится на полуинтервале сходится на полуинтервале  )
(Сообщение отредактировал RKI 30 сен. 2009 12:46)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 30 сен. 2009 12:05 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов