Revli8


Новичок
|
        
просвятите меня на ряд решаемый признаками сравнения, а то у меня не получается
n+1/(n+2)n
и 1/ln(n+1)
еще 1/(2n+1)! даламбера
(Сообщение отредактировал attention 10 дек. 2009 1:40)
|
Всего сообщений: 46 | Присоединился: октябрь 2008 | Отправлено: 2 июля 2009 18:55 | IP
|
|
Black_Star


Участник
|
        
Помогите, пожалуйста, исследовать на сходимость ряд
^n}{2}n\right)}{n^3+2})
(Сообщение отредактировал attention 10 дек. 2009 1:37)
|
Всего сообщений: 109 | Присоединился: ноябрь 2007 | Отправлено: 2 сен. 2009 18:04 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Black Star написал 2 сен. 2009 17:04
Помогите, пожалуйста, исследовать на сходимость ряд
^n}{2} n \right)}{n^3 + 2} )
Black Star, каждый нечетный член ряда равен нулю, т.е. 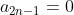 , а четный равен: , а четный равен:
^3 + 2})
Следовательно, имеем:
^n}{2} n \right)}{n^3 + 2} = \sum\limits_{n = 1}^\infty \frac{\arctan n}{(2n)^3 + 2} = \frac{1}{2}\sum\limits_{n = 1}^\infty \frac{\arctan n}{4n^3 + 1}. )
Теперь воспользуемся признаком Абеля.
Признак Абеля: Ряд  сходится, если сходится ряд сходится, если сходится ряд  , ,
а последовательность ) монотонна и ограничена. монотонна и ограничена.
В вашем примере положим
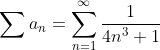
и 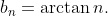
То, что 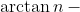 моннотонная и ограниченная последовательность, очевидно. моннотонная и ограниченная последовательность, очевидно.
Теперь осталось исследовать на сходимость ряд
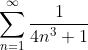
Это проще сделать, сравнив его с рядом
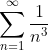
Мы можем сравнивать с данным рядом, т.к. члены данного ряда больше членов сравниваемого ряда.
А ряд обратных кубов сходится, согласно интегральному признаку Коши:
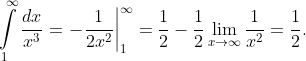
Следовательно, исходный ряд сходится согласно признаку Абеля.
P.S. Black Star, большая просьба, отредактируйте свой пост: вместо картинки вставте это
внешняя ссылка удалена
\infty\frac{\arctan\left(\frac{1+(-1)^n}{2}n\right)}{n^3+2}
И окружите это тэгами [IMG].
(Сообщение отредактировал attention 3 сен. 2009 11:18)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 2 сен. 2009 21:17 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Revli8 написал 2 июля 2009 17:55
просвятите меня на ряд решаемый признаками сравнения, а то у меня не получается

Revli8, здесь лучше использовать интегральный признак Коши:

Следовательно, ряд расходится согласно интегральному признаку Коши.
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 2 сен. 2009 22:54 | IP
|
|
sessia


Новичок
|
     
Помогите, пожалуйста, исследовать ряд на сходимость
+беск.
--
> (-1)^n*((3n+2)/sqrt^3(n^5+4))
--
n=1
Исследовала по признаку Лейбница, но на lim застряла..
(Сообщение отредактировал sessia 3 сен. 2009 17:25)
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 3 сен. 2009 17:19 | IP
|
|
Alex1990

Новичок
|
      
Здравствуйте. Помогите пожалуйста с задачей. Заранее спасибо.
оо
---
\
/ (x^n)/((2n-1)*3^n), найти область сходимости
---
n=1
|
Всего сообщений: 2 | Присоединился: сентябрь 2009 | Отправлено: 3 сен. 2009 18:02 | IP
|
|
attention 


Долгожитель
|
      
sessia и Alex1990, зайдите сюда

|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 3 сен. 2009 18:06 | IP
|
|
Alex1990

Новичок
|
      
Спасибо
|
Всего сообщений: 2 | Присоединился: сентябрь 2009 | Отправлено: 3 сен. 2009 18:09 | IP
|
|
attention 


Долгожитель
|
      
sessia, что именно не получается??
Если простая формула, то можно так (например, уравнение окружности): вводим в окно сообщения Форума ссылку, после неё формулу и окружвем это тэгами img, т.е. вводим это

Нажимеам отправить и получаем красивую картинку
^2+(y-b)^2=c^2 )
Напишите, что именно у Вас не получается!
sessia, во-первых, Вы неправильно набрали код формулы, поэтому интегралы, суммы, пределы и прочие сложные формулы лучше набирать в MathType так, как это объяснено в соответствующей теме.
(Сообщение отредактировал attention 10 дек. 2009 1:35)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 3 сен. 2009 20:59 | IP
|
|
sessia


Новичок
|
     

(Сообщение отредактировал sessia 3 сен. 2009 21:15)
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 3 сен. 2009 21:05 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов