attention 


Долгожитель
|
      
Зайдите в тему и сверьте установки MathType внимательно.
Лучше вставляйте формулы через радикал, но не забывайте
выбрать на радикале пункт Из интернета и туда уже вставляйте ссылку с формулой. По умолчанию на радикале стоит пункт С компьютера.
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 3 сен. 2009 21:16 | IP
|
|
sessia


Новичок
|
     
attention, спасибо за терпение, получилось наконец-то, помогите, пожалуйста, еще исследовать на сходимость  я пыталась по признаку Лейбница, но опять на lim застряла... я пыталась по признаку Лейбница, но опять на lim застряла...
(Сообщение отредактировал sessia 3 сен. 2009 21:20)
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 3 сен. 2009 21:19 | IP
|
|
attention 


Долгожитель
|
      
Цитата: sessia написал 3 сен. 2009 20:19
attention, спасибо за терпение, получилось наконец-то, помогите, пожалуйста, еще исследовать на сходимость

я пыталась по признаку Лейбница, но опять на lim застряла...
Воспользуемся признаком Лейбница:
Признак Лебница: Если ^{n}b_n, \, b_n\geqslant 0) и последовательность и последовательность ) , начиная с некоторого номера , начиная с некоторого номера  , монотонно стремится к нулю, то ряд , монотонно стремится к нулю, то ряд  сходится. сходится.

Следовательно, по признаку Лейбница ряд сходится.
(Сообщение отредактировал attention 3 сен. 2009 21:29)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 3 сен. 2009 22:14 | IP
|
|
Black_Star


Участник
|
        
Может, ли сумма ряда быть отрицательной? Если да, то что это значит?
|
Всего сообщений: 109 | Присоединился: ноябрь 2007 | Отправлено: 3 сен. 2009 22:56 | IP
|
|
attention 


Долгожитель
|
      
Black Star, у Вас кососая черта закрывающего тега не в ту сторону стоит, поэтому формула не преобразуется, надо
/IMG и, естественно, в квадратных скобках.
Насчет суммы ряда: может быть отрицательной, смотря как задан общий член.
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 3 сен. 2009 23:01 | IP
|
|
sessia


Новичок
|
     
attention, огромное Вам спасибо
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 4 сен. 2009 14:19 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Alex1990 написал 3 сен. 2009 17:02
Здравствуйте. Помогите пожалуйста с задачей. Заранее спасибо.
3^n} )
найти область сходимости
Сначала найдем интервал сходимости ряда

Теперь исследуем ряд на концах интервала сходимости )
В точке 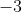 имеем следущий ряд: имеем следущий ряд:

который сходится условно, согласно признаку Лейбница:

В точке 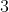 имеем ряд имеем ряд

который расходится, согласно интегральному признаку Коши:

(Сообщение отредактировал attention 5 сен. 2009 1:55)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 5 сен. 2009 2:54 | IP
|
|
Black_Star


Участник
|
        
Помогите пожалуйста найти сумму ряда 
|
Всего сообщений: 109 | Присоединился: ноябрь 2007 | Отправлено: 8 сен. 2009 0:15 | IP
|
|
attention 


Долгожитель
|
      
Цитата: Black Star написал 7 сен. 2009 23:15
Помогите пожалуйста найти сумму ряда 



(Сообщение отредактировал attention 8 сен. 2009 0:57)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 8 сен. 2009 1:52 | IP
|
|
sessia


Новичок
|
     
Помогите, пожалуйста, определить интервал сходимости функционального ряда и исследовать его сходимость на границах интервала

(Сообщение отредактировал sessia 8 сен. 2009 16:39)
|
Всего сообщений: 45 | Присоединился: июль 2009 | Отправлено: 8 сен. 2009 16:28 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов