JustSomebody
Новичок
|
     
Помогите. Очень нужно доказать, что ряд сходится (а он точно сходится).
Сумма от 1 до бесконечности sin(2pi/(2n+1))/n^(1/2)
Очень срочно.
|
Всего сообщений: 2 | Присоединился: март 2012 | Отправлено: 24 марта 2012 11:46 | IP
|
|
MEHT
Долгожитель
|
Признак Абеля или Дирихле.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 2 апр. 2012 17:51 | IP
|
|
muzgar
Новичок
|
Здравствуйте! Прошу помощи:
1. Найти интервал сходимости степенного ряда: сумм от 1до беск ((3^n*n!)/(n+1)^n)*x^n
2. вычислить опр.интеграл с точностью до 0.001, разложив подынтегральную ф-ю в ряд: интеграл от 0 до 0.5 ln(1+x^2)/x dx
|
Всего сообщений: 3 | Присоединился: апрель 2012 | Отправлено: 24 апр. 2012 9:54 | IP
|
|
MEHT
Долгожитель
|
1. Радиус сходимости будет обратным к пределу
^n%20})
при n стремящемся к бесконечности. Попробуйте найти самостоятельно.
2. Для логарифма воспользуйтесь рядом Маклорена
%20=%20t-%5Cfrac{t^2}{2}+%5Cfrac{t^3}{3}-%5Cfrac{t^4}{4}+...)
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 24 апр. 2012 18:35 | IP
|
|
muzgar
Новичок
|
MEHT, я первый по Даламберу решил. Получилось 3х/e. Потом саму точку проверил, ряд сходится, т.е. она входит в интервал. Так тоже можно?
2. во втором я сначала разложил ln(1+x), потом х заменил на х^2, потом поделил на х. Затем разбил интеграл на несколько частей, и проинтегрировал. сумма 4х членов дала ответ 0.234.... Записал ответ с точностью до тысячной, т.е. 0.234. Так все делаю?
|
Всего сообщений: 3 | Присоединился: апрель 2012 | Отправлено: 25 апр. 2012 6:30 | IP
|
|
MEHT
Долгожитель
|
Кстати, да. Тоже можно, только необходимо помнить, что ряд не числовой, а степенной.
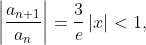
следовательно радиус сходимости R=e/3.
Строго говоря, проверять нужно обе точки x=e/3 и x=-e/3.
Но если, как Вы говорите, при e/3 есть сходимость, то для соответствующего ему знакопеременного ряда (при x=-e/3) сходимость будет и подавно.
2. Похоже на правду. Не забывайте только, что ряд логарифма сходится не для всех x. Ну, по крайней мере для вашего интервала (от 0 до 0.5) он вполне применим.
|
Всего сообщений: 1548 | Присоединился: июнь 2005 | Отправлено: 25 апр. 2012 14:01 | IP
|
|
muzgar
Новичок
|
спасибо 
|
Всего сообщений: 3 | Присоединился: апрель 2012 | Отправлено: 25 апр. 2012 15:08 | IP
|
|
monx
Новичок
|
Помогите. интервал сходимости ст ряда ∑_(n=2)^∞▒((〖2x〗^2n ))/(ln(4n+2)).
|
Всего сообщений: 2 | Присоединился: май 2012 | Отправлено: 6 мая 2012 14:01 | IP
|
|
monx
Новичок
|
отменяется, разобрался.
|
Всего сообщений: 2 | Присоединился: май 2012 | Отправлено: 6 мая 2012 16:22 | IP
|
|
vikusha81
Новичок
|
Народ, помогите плиз решить пример на сходимость ряда..... все решила, а с ним не могу разобраться =((
внешняя ссылка удалена
(Сообщение отредактировал vikusha81 14 мая 2012 23:53)
|
Всего сообщений: 3 | Присоединился: сентябрь 2010 | Отправлено: 14 мая 2012 23:53 | IP
|
|
Форум
2.1.17 Вопросы сходимости рядов
