imaginary


Новичок
|
     
Доброго времени суток уважаемые форумчане. Я столкнулся с таким вопросом как сравнение и применение различных признаков сходимости для положительных рядов(в дальнейшем просто рядов ).
Все мы знаем, что в каких-то случаях для доказательства сходимости(расходимости) рядов мы применяем различные признаки, в зависимости от ситуации, если ряд легко сравнить с рядом, сходимость которого известа,мы применим признак сравнения, если в ряде степени, корни, експоненты - мы используем радикальный признак Коши, если встречаются факториалы - Даламбера. При этом мы знаем, что,к примеру, признак Раабе сильнее признака Даламбера, но зачемтогда признак Даламбера?
Вот в подобном анализе состоит моя задача. Нужно привести примеры рядов, сходимость(расходимость) которых доказывается исключительно каким то признаком,допустим есть ряд,его сходимость(расходимость) доказывается признаком Коши-Макларена,а остальные признаки не могут дать ответа о данном ряде.
Нужно найти(привести,придумать) такие примеры. Я не преподавательи не часто сталкивался с такими примерами, но это очень нужно и важно.
Помогите пожалуйста найти такие примеры.
|
Всего сообщений: 1 | Присоединился: апрель 2010 | Отправлено: 28 апр. 2010 14:18 | IP
|
|
Lisa1811


Новичок
|
     
Помогите, пожалуйста, решить!
1 Найти интервал сходимости ряда, заданного общим членом
^{n} }{(n+2)3^{n} } )
(Сообщение отредактировал RKI 30 апр. 2010 9:27)
|
Всего сообщений: 2 | Присоединился: апрель 2010 | Отправлено: 29 апр. 2010 21:15 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Lisa1811 написал 29 апр. 2010 21:15
Помогите, пожалуйста, решить!
1 Найти интервал сходимости ряда, заданного общим членом
^{n} }{(n+2)3^{n} } )
(Сообщение отредактировал RKI 30 апр. 2010 9:27)
1. Радиус сходимости данного степенного ряда находите по формуле: 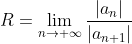
Следовательно, ряд будет сходиться на интервале  )
2. Далее изучаете поведение ряда в граничных точках 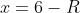 и и 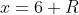
В каждой из граничных точках ряд примет некоторый вид (либо с положительными членами либо знакопеременный). Для опредедления их сходимости надо будет воспользоваться соответствующими признаками (сравнения, Даламбера, Коши, Лейбница, Коши-Макларена и так далее)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 30 апр. 2010 9:33 | IP
|
|
nodya

Новичок
|
      
Народ, помогите пожалуйста! заранее спасибо)
Исследовать сходимость ряда:
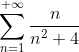
(Сообщение отредактировал RKI 30 апр. 2010 17:32)
|
Всего сообщений: 13 | Присоединился: март 2010 | Отправлено: 30 апр. 2010 17:28 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: nodya написал 30 апр. 2010 17:28
Народ, помогите пожалуйста! заранее спасибо)
Исследовать сходимость ряда:
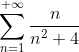
(Сообщение отредактировал RKI 30 апр. 2010 17:32)
Для исследования сходимости данного ряда подойдут лишь признаки сравнения
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 30 апр. 2010 17:33 | IP
|
|
nodya

Новичок
|
      
a kakie imenno, 4to mne ispolzovat?
|
Всего сообщений: 13 | Присоединился: март 2010 | Отправлено: 30 апр. 2010 19:29 | IP
|
|
attention 


Долгожитель
|
      
Цитата: RKI написал 30 апр. 2010 17:33
Цитата: nodya написал 30 апр. 2010 17:28
Народ, помогите пожалуйста! заранее спасибо)
Исследовать сходимость ряда:
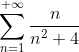
Для исследования сходимости данного ряда подойдут лишь признаки сравнения
RKI, здесь очень просто применить интегральный признак Коши, и получим, что ряд расходится, так как расходится несобственный интеграл, составленный из его общего члена.
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 1 мая 2010 15:25 | IP
|
|
alien1991

Новичок
|
      
Помогите,пожалуйста. В понедельник сдавать контрольную.
Исследовать на абсолютную условную сходимость ряда
^{n+1}}{10n+1}.)
(Сообщение отредактировал attention 8 мая 2010 12:54)
|
Всего сообщений: 2 | Присоединился: май 2010 | Отправлено: 8 мая 2010 11:24 | IP
|
|
attention 


Долгожитель
|
      
Цитата: alien1991 написал 8 мая 2010 11:24
Помогите,пожалуйста. В понедельник сдавать контрольную.
Исследовать на абсолютную условную сходимость ряда
^{n+1}}{10n+1}.)
Очевидно, что условно ряд сходится (согласно признаку сходимости знакопеременных рядов Лейбница).
Согласно интегральному признаку Коши, абсолютно ряд расходится,:
}{10x+1}=\hfill\\\\=\left.{\frac{1}{10}\lim_{b\to\infty}\ln(10x+1)}\right|_1^b=\frac{1}{10}\lim_{b\to\infty}\Bigl(\ln(10b+1)-\ln11\Bigl)=\infty.\hfill\\\end{gathered})
(Сообщение отредактировал attention 8 мая 2010 12:55)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 8 мая 2010 12:51 | IP
|
|
alien1991

Новичок
|
      
Я вам очень благодарна!!!
|
Всего сообщений: 2 | Присоединился: май 2010 | Отправлено: 8 мая 2010 13:44 | IP
|
|
|

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов