arinka1982

Новичок
|
     
Спасибо,но уже пробовала. По признаку Даламбера в точке х=2 предел равен 1. А вот по другому решить не получается... Поэтому прошу помощи!!!
Задание:

Найти радиус и интервал сходимости. Помогите, пожалуйста, исследовать на концах интервала (-2;2). Если использовать признак Даламбера, то при х=2, предел равен 1. А другими способами ну никак не получается !
(Сообщение отредактировал attention 18 фев. 2010 14:59)
|
Всего сообщений: 4 | Присоединился: февраль 2010 | Отправлено: 16 фев. 2010 9:22 | IP
|
|
ProstoVasya

Долгожитель
|
     
arinka1982
Воспользуйтесь формулой Стирлинга для факториала.
Получите оценку модуля общего члена, из которой будет следовать абсолютная сходимость ряда.
|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 18 фев. 2010 7:59 | IP
|
|
arinka1982

Новичок
|
     
Если я правильно поняла, то по формуле Стирлинга  Тогда привести всё это к нормальному виду ну никак не получается. Может я неправильно воспользовалась формулой Стирлинга? Тогда привести всё это к нормальному виду ну никак не получается. Может я неправильно воспользовалась формулой Стирлинга?
|
Всего сообщений: 4 | Присоединился: февраль 2010 | Отправлено: 18 фев. 2010 23:17 | IP
|
|
attention 


Долгожитель
|
      
arinka1982, попробуйте воспользоваться признаком Раабе:
^2}{(2n + 2)!}. \hfill \\ \\a_n = \frac{4^n\left(n!\right)^2}{(2n + 2)!} = \frac{4^n\left(n!\right)^2}{(2n)!(1 + 2n)(2 + 2n)} \Rightarrow \hfill \\ \Rightarrow a_{n + 1} = \frac{4^{n + 1}\left((n + 1)!\right)^2}{(2n + 4)!} = \frac{4 \cdot 4^n\left(n!\right)^2(n + 1)^2}{(2n)!(1 + 2n)(2 + 2n)(3 + 2n)(4 + 2n)}. \hfill \\ \\ \mathop {\lim}\limits_{n \to \infty} n\left(\frac{a_n}{a_{n + 1}} - 1\right) = \mathop {\lim}\limits_{n \to \infty} n\left(\frac{(3 + 2n)(2 + n)}{2(n + 1)^2} - 1\right) = \frac{1}{2}\mathop {\lim}\limits_{n \to \infty} \frac{3n^2 + 4n}{(n + 1)^2} = \hfill \\ = \frac{1}{2}\mathop {\lim}\limits_{n \to \infty } \frac{3 + \frac{4}{n}}{\left(1 + \frac{1}{n}\right)^2} = \frac{1}{2}\mathop {\lim}\limits_{n \to \infty} \frac{3 + 0}{(1 + 0)^2} = \frac{3}{2} > 1. \hfill \\ \end{gathered})
Так как предел больше единицы, то, следовательно, согласно признаку Раабе, данный ряд сходится.
(Сообщение отредактировал attention 19 фев. 2010 16:08)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 19 фев. 2010 6:07 | IP
|
|
ProstoVasya

Долгожитель
|
     
arinka1982

|
Всего сообщений: 1268 | Присоединился: июнь 2008 | Отправлено: 19 фев. 2010 19:30 | IP
|
|
d1993r

Новичок
|
      

|
Всего сообщений: 2 | Присоединился: февраль 2010 | Отправлено: 23 фев. 2010 21:48 | IP
|
|
Stalker


Новичок
|
       
Вычислить определенный интеграл с точностью до 0,001. Для этого подынтегральную функцию разложить в степенной ряд, который затем почленно проинтегрировать:

|
Всего сообщений: 5 | Присоединился: март 2010 | Отправлено: 3 марта 2010 17:02 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Stalker написал 3 марта 2010 17:02
Вычислить определенный интеграл с точностью до 0,001. Для этого подынтегральную функцию разложить в степенной ряд, который затем почленно проинтегрировать:

 = \sum\limits_{n=1}^{+\infty} \frac{(-1)^{n+1}y^{n} }{n} )
 = \sum\limits_{n=1}^{+\infty} \frac{(-1)^{n+1}(-x^{2})^{n} }{n} = \sum\limits_{n=1}^{+\infty} \frac{(-1)^{n+1}(-1)^{n}x^{2n} }{n} = \sum\limits_{n=1}^{+\infty} \frac{(-1)^{2n+1}x^{2n} }{n} = )
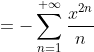
 = - \sum\limits_{n=1}^{+\infty} \frac{x^{2n+1} }{n} )
dx = -\int \sum\limits_{n=1}^{+\infty} \frac{x^{2n+1} }{n} dx = - \sum\limits_{n=1}^{+\infty} \int\frac{x^{2n+1}dx}{n} = - \sum\limits_{n=1}^{+\infty} \frac{x^{2n+2} }{n(2n+2)} )
 = - \sum\limits_{n=1}^{+\infty} \frac{x^{2n+2} }{n(2n+2)} )
 = 0 )
 = - \sum\limits_{n=1}^{+\infty} \frac{(0.5)^{2n+2} }{n(2n+2)} = - \sum\limits_{n=1}^{+\infty} \frac{(0.25)^{n+1} }{2n(n+1)} )
dx = F(0.5) - F(0) = - \sum\limits_{n=1}^{+\infty} \frac{(0.25)^{n+1} }{2n(n+1)} \sim )
Отбрасываем при вычислении все слагаемые, начиная со слагаемого, меньшего по абсолютной величине 0,001
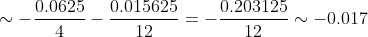
(Сообщение отредактировал RKI 5 марта 2010 16:05)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 5 марта 2010 15:54 | IP
|
|
korp


Новичок
|
     
Помогите пожалуйста, ото болел а сейчас рейтинг и ни как не пойму тему.
1. Найти область сходимости данного функционального ряда:
^n}{(n+4)ln(n+4)})
2. Найти радиус, интервал и область сходимости степенного ряда, иследовав его поведение на концах интервала сходимости:
^n%5Ccdot%20n^2%20}{2^2^n^+^1})
|
Всего сообщений: 3 | Присоединился: март 2010 | Отправлено: 16 марта 2010 23:37 | IP
|
|
sergeernie


Новичок
|
       
Здравствуйте, помогите пожалуйста

|
Всего сообщений: 1 | Присоединился: апрель 2010 | Отправлено: 14 апр. 2010 11:43 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов