jul

Новичок
|
     
Спасибо большое!!!
|
Всего сообщений: 2 | Присоединился: декабрь 2009 | Отправлено: 18 дек. 2009 16:48 | IP
|
|
Studentka

Новичок
|
     
помогите исследовать ряды на сходимости...

|
Всего сообщений: 2 | Присоединился: декабрь 2009 | Отправлено: 18 дек. 2009 22:23 | IP
|
|
kuk3d

Новичок
|
     
Народ помогите плиз решить примерчик:

(Сообщение отредактировал kuk3d 18 дек. 2009 22:40)
|
Всего сообщений: 3 | Присоединился: декабрь 2009 | Отправлено: 18 дек. 2009 22:40 | IP
|
|
ProLL

Новичок
|
     
Здраствуйте! Помогите, пожалуйста, с примером, а то я запутался что-то, когда предел вычислял...

(Сообщение отредактировал ProLL 21 дек. 2009 18:51)
|
Всего сообщений: 2 | Присоединился: декабрь 2009 | Отправлено: 21 дек. 2009 18:50 | IP
|
|
BogatoFF


Новичок
|
        
помоги те пожалуйста найт интеграл сходимотсти степенного ряда и исследовать на сходимость(абсолютную и условную) в концах интервала сходимости:
беск
summ 5n-1/корень:n+n^2 закр.корень (х-1)^n очень нужно благодарю заранее!
n=1
|
Всего сообщений: 1 | Присоединился: январь 2010 | Отправлено: 19 янв. 2010 15:15 | IP
|
|
Alleks


Новичок
|
     
Помогите Исследовать на сходимость интеграл
int sin (5x^2)/2 от -0,4 до 0
|
Всего сообщений: 23 | Присоединился: март 2009 | Отправлено: 3 фев. 2010 7:13 | IP
|
|
Snigur


Новичок
|
     
Помогите с заданием
найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала. Написать три первых числа степенного ряда
(3^n*х^n)/(2^n+5^n)
|
Всего сообщений: 19 | Присоединился: июль 2009 | Отправлено: 9 фев. 2010 19:28 | IP
|
|
RKI 


Долгожитель
|
     
Цитата: Snigur написал 9 фев. 2010 19:28
Помогите с заданием
найти интервал сходимости ряда и исследовать его сходимость на концах этого интервала. Написать три первых числа степенного ряда
(3^n*х^n)/(2^n+5^n)

Найдем радиус 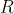 сходимости степенного ряда. сходимости степенного ряда.
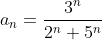
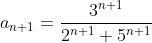
}{3^{n+1}(2^{n} + 5^{n})} = )
} = \lim\limits_{n \to + \infty} \frac{5^{n+1}((\frac{2}{5})^{n+1} + 1)}{5^{n}3((\frac{2}{5})^{n} + 1)} = )
^{n+1} + 1)}{3((\frac{2}{5})^{n} + 1)} = \frac{5(0+1)}{3(0+1)} = \frac{5}{3} )
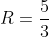

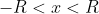
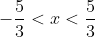
Таким образом, исходный степенной ряд  сходится на интервале сходится на интервале . )
Рассмотрим граничные точки 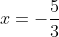 и и 
При 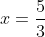 исходный ряд исходный ряд  принимает вид принимает вид 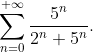
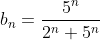
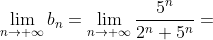
^{n} + 1} = \frac{1}{0+1} = 1 )
Общий член ряда 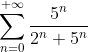 не стремится к нулю. Следовательно, числовой ряд не стремится к нулю. Следовательно, числовой ряд 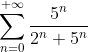 является расходящимся. Таким образом, исходный степенной ряд является расходящимся. Таким образом, исходный степенной ряд  в точке в точке 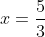 расходится. расходится.
При  исходный ряд исходный ряд  принимает вид принимает вид ^{n} 5^{n} }{2^{n} + 5^{n} }. )
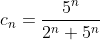
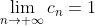
Таким образом, нарушается необходимое условие теоремы Лейбница. Это означает, что знакопеременный ряд ^{n} 5^{n} }{2^{n} + 5^{n} } ) является расходящимся. Следовательно, исходный степенной ряд является расходящимся. Следовательно, исходный степенной ряд  в точке в точке  расходится. расходится.
В итоге степенной ряд  сходится на интервале сходится на интервале . )
(Сообщение отредактировал RKI 10 фев. 2010 11:02)
|
Всего сообщений: 5184 | Присоединился: октябрь 2008 | Отправлено: 10 фев. 2010 10:27 | IP
|
|
arinka1982

Новичок
|
     
Добрый вечер! Задание такое:Найти интервал и радиус сходимости ряда:

Радиус нашла, используя признак Даламбера, соответсвенно нашла и интервал (-2;2), а вот исследовать на концах интервала никак не могу. Помогите, пожалуйста.
|
Всего сообщений: 4 | Присоединился: февраль 2010 | Отправлено: 15 фев. 2010 23:25 | IP
|
|
attention 


Долгожитель
|
      
arinka1982, попробуйте также воспользоваться признаком Даламбера.
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 16 фев. 2010 1:38 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов