Bacara

Новичок
|
     
Помогите пожалуйста исследовать ряд на сходимость:
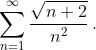
Необходимо очень срочно. Заранее благодарю...
(Сообщение отредактировал attention 10 дек. 2009 1:07)
|
Всего сообщений: 1 | Присоединился: декабрь 2009 | Отправлено: 9 дек. 2009 22:28 | IP
|
|
attention 


Долгожитель
|
      
Цитата: lola36 написал 8 дек. 2009 21:54
Помогите исследовать на сходимость ряды......Заранее балгодарю))))
^n\!\left(\frac{1}{n}\right)^7.)
Воспользуемся признаком Абеля.
Признак Абеля: Ряд  сходится, если сходится ряд сходится, если сходится ряд  , а последовательность , а последовательность ) монотонна и ограничена. монотонна и ограничена.
В вашем примере положим
^7},\, b_n = \left(\frac{7}{8}\right)^n.)
То, что 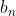 моннотонная и ограниченная последовательность, очевидно моннотонная и ограниченная последовательность, очевидно
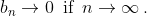
Теперь осталось исследовать на сходимость ряд
^7 .)
А этот ряд сходится, согласно интегральному признаку Коши:
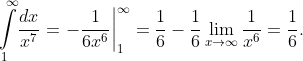
Следовательно, исходный ряд сходится согласно признаку Абеля.
Цитата: lola36 написал 8 дек. 2009 21:54
Помогите исследовать на сходимость ряды......Заранее балгодарю))))
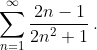
Воспользуемся интегральным признаком Коши:

Следовательно, согласно интегральному признаку Коши, исходный ряд расходится, т.к. расходится интеграл, составленный из общего члена данного ряда.
Цитата: lola36 написал 8 дек. 2009 21:54
Помогите исследовать на сходимость ряды......Заранее балгодарю))))
^{n + 1} }{\ln n} .)
Условно ряд сходится по признаку Лейбница, т.к.

Абсолютно ряд расходится, по признаку сравнения, т.к. абюсолютные членны данного ряда больше членов гармонического ряда, который, как известно, расходится:
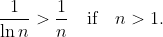
Изначальный ряд сходится условно, но абсолютно расходится.
Цитата: lola36 написал 8 дек. 2009 21:54
Помогите исследовать на сходимость ряды......Заранее балгодарю))))
^{n + 1} }{n^2 + 1} .)
Ряд сходится условно, по признаку Лейбница, т.к.
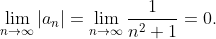
Также ряд сходится и абсолютно, по интегральному признаку Коши, т.к.
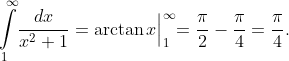
(Сообщение отредактировал attention 10 дек. 2009 4:49)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 10 дек. 2009 2:02 | IP
|
|
lola36


Новичок
|
       
Цитата: attention написал 10 дек. 2009 1:02
Спасибочки огромное.......Очень благодарна за Ваши ответы.........буду на этот форум частенько наведоваться!!!!!!
|
Всего сообщений: 3 | Присоединился: декабрь 2009 | Отправлено: 11 дек. 2009 23:35 | IP
|
|
dini

Новичок
|
     
Помогите, пожалуйста, исследовать сходимость ряда:

И еще один ряд исследовать на сходимость:

Заранее благодарю!
(Сообщение отредактировал attention 12 дек. 2009 17:25)
|
Всего сообщений: 47 | Присоединился: март 2007 | Отправлено: 12 дек. 2009 12:25 | IP
|
|
Kmary


Новичок
|
     

Исследовать на сходимость.
Математик сказал что задачи довольно сложные. Сама решить не смогла.
Вот.
(Сообщение отредактировал Kmary 16 дек. 2009 18:50)
|
Всего сообщений: 1 | Присоединился: декабрь 2009 | Отправлено: 16 дек. 2009 18:31 | IP
|
|
rkit

Новичок
|
     
Цитата: dini написал 12 дек. 2009 12:25
Помогите, пожалуйста, исследовать сходимость ряда:

И еще один ряд исследовать на сходимость:

Заранее благодарю!
(Сообщение отредактировал attention 12 дек. 2009 17:25)
1. Признак д’Аламбера: /frac{a_{n+1}}{a_n}=/frac{(n+1)(2n+2+1)}{3n+3} > 1 - расходится
2. /sqrt{n^2-4n+1} начинает возрастать, когда n^2>4n - сходится по признаку Лейбница
(Сообщение отредактировал rkit 16 дек. 2009 19:52)
|
Всего сообщений: 1 | Присоединился: декабрь 2009 | Отправлено: 16 дек. 2009 19:51 | IP
|
|
lola36


Новичок
|
       
Помогите исследовать на сходимость ряды....и найти область сходимости ряда......Заранее балгодарю))))

(Сообщение отредактировал attention 18 дек. 2009 1:39)
|
Всего сообщений: 3 | Присоединился: декабрь 2009 | Отправлено: 17 дек. 2009 22:10 | IP
|
|
jul

Новичок
|
     
Здравствуйте! Помогите пож-та!!! нужно найти интервал сходимости степенного ряда
 x^n}{4^n \sqrt{n + 5}})
Решала ряд принципом Даламбера, получилось что ряд абсолютно сходится на интервале -4/5<x<4/5
запуталась в сходимости ряда на концах интервала, при x=-4/5 и при x=4/5
не поможете разобраться?
(Сообщение отредактировал attention 19 фев. 2010 15:19)
|
Всего сообщений: 2 | Присоединился: декабрь 2009 | Отправлено: 17 дек. 2009 22:19 | IP
|
|
Tom

Новичок
|
      
Ребят срочно помогите решить эти примеры, хоть один.
Вот фото

Заранее благодарю!
(Сообщение отредактировал attention 18 дек. 2009 1:36)
|
Всего сообщений: 1 | Присоединился: декабрь 2009 | Отправлено: 17 дек. 2009 22:45 | IP
|
|
attention 


Долгожитель
|
      
Цитата: jul написал 17 дек. 2009 21:19
Здравствуйте! Помогите пож-та!!! нужно найти интервал сходимости степенного ряда
 x^n}{4^n \sqrt{n + 5} })
Решала ряд принципом Даламбера, получилось что ряд абсолютно сходится на интервале -4/5<x<4/5
запуталась в сходимости ряда на концах интервала, при x=-4/5 и при x=4/5
не поможете разобраться?
x^n}{4^n\sqrt {n + 5} } \Rightarrow a_{n + 1} = \frac{\left(5^{n +1} + 1\right) x^{n + 1} }{4^{n + 1}\sqrt {n + 6} } = \frac{x}{4}\frac{\left(5 \cdot 5^n + 1\right)x^n}{4^n\sqrt {n + 6} }. \hfill \\ \frac{a_{n + 1} }{a_n} = \frac{x}{4} \frac{\left(5 \cdot 5^n + 1\right)x^n}{4^n\sqrt{n + 6} }:\frac{\left(5^n + 1\right) x^n}{4^n\sqrt{n + 5} } = \frac{x}{4}\frac{\left( 5 \cdot 5^n + 1 \right) \sqrt {n + 5} }{\left(5^n + 1\right)\sqrt {n + 6} }. \hfill \\ \end{gathered} )
\sqrt {n + 5} }{\left(5^n + 1\right)\sqrt {n + 6} } = \frac{|x|}{4}\mathop {\lim }\limits_{n \to \infty}\frac{\left(5 + \frac{1}{5^n} \right)\sqrt {1 + \frac{5}{n} } }{\left(1 + \frac{1}{5^n} \right)\sqrt {1 + \frac{6}{n} } } = \hfill \\ = \frac{|x|}{4}\frac{(5 + 0)\sqrt {1 + 0} }{(1 + 0)\sqrt{1 + 0} } = \frac{5}{4}\left| x \right| < 1 \Leftrightarrow |x| < \frac{4}{5} \Leftrightarrow - \frac{4}{5} < x < \frac{4}{5}. \hfill \\ \end{gathered})
Теперь исследуем ряд на концах интервала сходимости:
1) в точке –4/5 имеем
^n = \sum\limits_{n = 1}^\infty\!\frac{(-1)^n\left(5^n + 1\right)}{5^n\sqrt {n + 5} } )
По признаку Лейбница, данный ряд сходится, т.к.
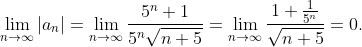
2) в точке 4/5 имеем
^n = \sum\limits_{n = 1}^\infty\!\frac{5^n + 1}{5^n\sqrt {n + 5} } = \sum\limits_{n = 1}^\infty\!\frac{1}{\sqrt {n + 5} } + \sum\limits_{n = 1}^\infty\!\frac{1}{5^n\sqrt {n + 5} } .)
Так как первый ряд  расходится, по интегральному признаку Коши: расходится, по интегральному признаку Коши:

То, следовательно, расходится и ряд 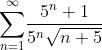 . .
(Сообщение отредактировал attention 18 дек. 2009 18:07)
|
Всего сообщений: 994 | Присоединился: апрель 2006 | Отправлено: 18 дек. 2009 9:14 | IP
|
|

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов

 Форум
Форум

 Математика
Математика

 2.1.17 Вопросы сходимости рядов
2.1.17 Вопросы сходимости рядов